TEST PAPER - 1
Section - A (Attempt all questions)
Question 1: Choose the correct answers to the question from the given options: (15)
i) A Dealer in Mumbai sold a washing machine to a consumer in Mumbai for Rs18000. If the rate of GST is 18%, then SGST is
a) Rs1620 b) Rs3240 c) nil d) none
ii) Roots of the equation 3x²- 2√6x + 2=0 are:
a) ±√(2/3) b) √(2/3), √(2/3) c) - √(2/3) , -√(2/3) d) -√(2/3) , -√(3/2)
iii) if x - 2 is a factor of x²- 7x + 2m, then the value of m is
a) 5 b) 6 c) 4 d) 3
iv) The transpose of the matrix
1 5 4
-2 1 6 is
a) 1 -2 b) -2 1 6 c) 1 -2 d) 4 5 1
5 1 1 5 4 5 1 -6 1 -2
-2 6 4 6
v) 21% Rs 100 shares at Rs 140 gives rate of return as:
a) 10% b) 120% c) 15% d) 25%
vi) The Reflection of the point P(0,3) in the y-axis is:
a) (0,-3) b) (3,0) c) (0, 3) d) (0,0)
The length of AD is:
a) 12cm b) 14cm c) 16 cm d) 18 cm
viii) Richa attaches a conical attachment to one side of the coin. The radius of coin and conical attachment is same. Which of the following is the surface area of the combined solid ?
a) coin base area + coin CSA
b) coin base area + coin CSA + cone CSA
c) total surface area of coin + total surface area cone.
d) total surface area of cone.
ix) Which term of the GP 18, 12, 8, ...., is 512/729 ?
a) 9th b) 10th c) 11th d) 12th
x) if a coin is tossed 3 times, what is the probability of getting a tail each time ?
a) 1/8 b) 1/4 c) 1/16 d) 1/6
xi) Two similar jugs have heights of 4cm and 6cm respectively. If the capacity of the smaller jug is 48 cm³, then the capacity of the larger jug is:
a) 100 cm⅔ b) 130cm³ c) 152cm³ d) 162cm²
xii) x-axis divides the line segment joining the points (2,-3) and (5,6) in the ratio.
a) 1:2 b) 2:1 c) 3:5 d) 2:3
xiii) In the given figure,O is the centre of the circle. If Angle OAB=40°, then angle ACB is equal to
a) 50° b) 40° c) 60° d) 70°
xiv) The sum of the first 16 terms of the AP is 10, 6, 2,.... is
a) -320 b) 320 c) -350 d) -300
xv) Assertion (A): The median of the following: 12.5, 12, 13, 15, 11, 12, 14, 16, 10, 12, 13
Reason (R): The value of the middle most observation obtained after arranging the data in an ascending and descending order is called the medium of the data
a) A is true, R is false
b) A is false, R is true
c) both A and R are true
d) both A and R are false
Question 2:
i) A conical tent is to accommodate 77 perso. Each person must have 16 m³ of air to breathe. Given the radius of the tent as 7m, find the height of the tent and also its curved surface area. (4)
ii) Amit Kumar invests Rs 36000 in buying Rs100 shares at Rs20 premium. The dividend is 15% per annum. Find :
a) the number of shares he buys.
b) his yearly dividend.
c) the percentage return on his investment. (4)
iii) The sum of three numbers in GP is 35 and their product is 1000. Find the numbers . (4)
Question 3:
i) Pawan deposituRs 150 every month in a bank for 8 months under the recurring deposit scheme. Find the maturity value of his deposit, if the interest is calculated every month and the rate of the interest is 8% per annum. (4)
ii) Find the equation of a line passing through the point (-2,3) and having the x-intercept of 4 units. (4)
iii) Use graph paper to solve this question.
a) Plot the points P(0,3), Q(3,-2) and O(0,0) .
b) Plot R, the image of Q, when reflected in the y-axis and write its coordinates.
c) What is the geometrical name of the figure PQOR ? (5)
SECTION - B
(Attempt any four questions from this section)
Question 4:
i) A dealer is Patna (Bihar) supplies goods worth Rs 15000 to a dealer in Sonipat (Haryana). The dealer in Sonepat supplies the same goods to a dealer in Rohtak (Haryana) at a profit of Rs3000. If the rate GST is 18%. calculate:
a) The cost of goods to the dealer in Rohtak.
b) Net GST paid by the dealer in Sonepat . (3)
ii) Solve the equation 4x²- 5x -3=0 and give your answer to correct to two decimal places. (3)
iii) On a map drawn to a scale if 1: 250000, a triangular plot of land has the following measurements. AB= 3cm, BC =4 cm and angle ABC=90°. Calculate
a) the actual length of AB in km.
b) the area of the plot in km². (4)
Question 5:
i) If A= 0 -1 B= 1 3 C= 1 0
2 5 6 4 -3 -2
find A(B + C). (3)
ii) Two circles touch externally at P. a tangent touches the circles at A and B. Prove that the tangent at P bisects AB. (3)
iii) The polynomial (px³+ 3x²-3) and (2x³- 5x +p) when divided by (x -4) leave the same reminder. Find the value of p. (4)
Question 6:
i) Find the coordinates of the point of trisection of the line segment joining the points A(5,-3), and B( 2,-9). (3)
ii) Prove that: cotA - tanA = (2cos²A -1)/(sinA cosA). (3)
iii) How many terms of the AP 72, 66, 60,..... must be taken to give the sum 0 ? (4)
Question 7:
i) The daily wages of 80 workers in a project ate given below:
Wages No. Of workers
400-450 2
400-500 6
500-550 12
550-600 18
600-650 24
650-700 13
700-750 5
Use a graph paper to draw an ogive for the above distribution, (use a scale of 2cm = Rs50 on x-axis and 2cm= 10 workers on yaxr). Use your ogive to estimate :
a) the median wagy of the workers .
b) the lower quartile wage of workers.
c) the number of workers who earns more than Rs625 daily. (5)
ii) A bus covers distance of 240 km at a uniform speed. Due to heavy rain its speed gets reduced by 10 km/hr and as such it takes two hours longer to cover the total distance. Assume the uniform speed to be x km/hr, form an equation and solve it to evaluate x. (5)
Question 8:
i) In a lottery there are 5 prizes and 20 blanks. What is the probability getting a prize ? (3)
ii) Construct a quadrilateral ABCD which AB= 5cm, BC= 4cm, angle B= 60°, AD= 5.5cm and D is equidistant from AB and BC. (3)
iii) In the given figure,PQ is a tangent to the circle at A. AB and AD are bisectors of angle CAQ and angle PAC. If Angle BAQ= 30°, show that
a) BD is a diameter of the circle.
b) ABC is an isosceles triangle. (4)
Question 9:
i) Solve the following inequation and graph the solution set on the number line:
-1/5 ≤ 3x/10 +1 < 2/5, x ∈ R. (3)
ii) Calculate the mean of the following distribution using step deviation method.
Marks no.of students
00-10 10
10-20 9
20-30 25
30-40 30
40-50 16
50-60 10 (3)
iii) In the figure,ABCD is a parallelogram. P is a point on BC such that BP: PC= 1:2. DP produced meets produced at Q. Given ar(∆CPQ) is 20 m², find
a) ar(∆ DCP)
b) ar(|| gm ABCD). (4)
Question 10:
i) using properties of proportion, solve for x. Given that x is positive:
{2x + √(4x²-1)}/{2x - √(4x²-1)}= 4. (3)
ii) Draw a circle with centre O and radius 3.1cm. Take a point P outside the circle at a distance of 6.2cm from its Centre. Draw two tangents to the circle from the point P. (3)
iii) An aeroplane at an altitude of 1500 metres finds that two ships are selling towards it in the same direction. The angles of depression as observed from the aeroplane are 45° and 30° respectively. Find the distance between the two ships. (4)
GOODS AND SERVICES TAX
Multiple Choice Questions
1) IGST is charged on:
a) interstate transaction b) intrastate transaction c) both a, b d) none
2) GST payable is equals to
a) ITC --output GST b) output GST + ITC c) output GST - ITC d) output GST
3) A dealer in Mumbai sold a washing machine to a consumer in Mumbai for Rs18000. If the rate of GST is 18% and GST, then SGST is:
a) Rs1620 b) Rs3240 c) nil d) none
4) In a transaction from Delhi to Lucknow, MRP = Rs10000, discount= 10%, GST= 28%. Here IGST is:
a) Rs2520 b) Rs5040 c) nil d) none
5) A refrigerator was sold for Rs15000 under intrastate transaction from station A to station B and the GST rate is 18%. CGST is:
a) Rs1450 b) Rs 1350 c) Rs1300 d) Rs2700
6) A dealer purchased goods worth Rs 15000 and sold them for Rs21000 within the state. If the rate of GST is 12%, then the net SGST paid by the dealer is:
a) Rs360 b) Rs720 c) Rs800 d) Rs850
7) A dealer in Delhi sold a water heater whose marked is Rs22000 to a customer in Delhi at discount of 25%. If the rate of GST 18%, then the SGST paid is:
a) Rs 1485 b) Rs2970 c) Rs1980 d) nil
8) Anushka bought 400g of almonds at Rs1200 per kg. If the rate of GST is 5%, the amount paid by Anushka is:
a) Rs504 b) Rs480 c) Rs1260 d) Rs630
9) A dealer in Agra sold an LED to a customer in Agra for Rs28000. If SGST is Rs2420, then the rate of GST is:
a) 12% b) 18% c) 9% d)28%
10) Mr. Sharma purchased goods worth Rs40000 from a dealer(within the same state ). If the rate of GST 18%, then CGST is:
a) Rs 3600 b) Rs7200 c) Rs8000 d) nil
11) The tax invoice of a mobile company in Delhi shows cost of services provided by it as Rs1200. If the rate of GST is 18%, then amount of the bill is:
a) Rs 1400 b) Rs1308 c) Rs 1416 d) Rs1500
12) A shopkeeper in Rampur sold an oven to a customer in Rampur for Rs26400. If the rate of GST is 28%, then IGST is:
a) Rs3696 b) Rs7392 c) Rs1848 d) nil
13) A dealer in Bhopal (MP) supplies goods worth Rs 30000 to a dealer in Delhi. The dealer in Delhi supplies the same goods to a customer in Delhi at a profit of Rs5000. If the rate of GST is 18%, then the net GST paid by the dealer in Delhi is:
a) Rs900 b) Rs2700 c) Rs5400 d) nil
14) A dealer in Patna (Bihar) supplies goods worth Rs 15000 to a dealer in Sonepat(Haryana). The dealer in Sonepat supplies the same goods to a dealer in Rohtak (Haryana) at a profit of Rs 3000. If the rate of GST is 18%, then the net GST paid by the dealer in Sonepat is:
a)Rs 540 b) Rs700 c) Rs720 d) nil
15) A retailer purchases an iron for Rs1500 from a dealer and sells it to a consumer at 10% profit. If the sales and intrastate , and the rate of GST is 12%, then the selling price of the iron including GST by the retailer is:
a)!Rs1550 b) Rs1848 c) Rs1950 d) Rs
16) A shopkeeper purchased a fan for Rs1500 from a dealer and sold it to a customer at 10% profit. If the sells are intrastate and the rate of GST is 12%, then the tax (under GST) received by the central government is :
a) Rs18 b) Rs99 c) Rs198 d) nil
17) Goods from Delhi are sold to Ranchi(Jharkhand) for Rs20000 and then from Ranchi to Cuttack (Odisha). If the rate of GST is 18%, and the profit made at Ranchi is Rs5000, then the net GST payable by the dealer in Ranchi is :
a) Rs1000 b) Rs900 c) Rs850 d) Rs875
18) A shopkeeper bought an article from a dealer at Rs1000. He sold it to the customer at Rs1200. If the rate of GST is 12%, then the amount paid by the customer to buy the item is:
a) Rs 1200 b) Rs1300 c) Rs1344 d) Rs1350
19) Three friends A, B and C live in Delhi. A sales medicine worth Rs50000 to B, B sells the same medicine to C at a profit of Rs 6000. If the rate of GST is 12%, then SGST paid by B is:
a) Rs300 b) Rs360 c) Rs400 d) Rs425
20) Mr Gupta wanted to book a semidelux room in a hotel for Rs750. Since semidelux room was not available, he booked a delux room for Rs1400. If GST for a room below Rs1000 is 18% and GST for a room above Rs1000 is 28%, then the extra GST paid by Mr Gupta for the delux room is:
a) Rs 257 b) Rs280 c) Rs300 d) Rs425
Answer:
1a 2c 3a 4a 5b 6a 7a 8a 9b 10a 11c 12 d 13 a 14a 15b 16b 17b 18c 19b 20a
Short Answer Type Questions:
1) Find the amount of bill for the following intrastate transaction of goods , if the GST rate is 28%.
items I II III
Marked price(Rs) 7000 14700 28200
discount% 20 10 10
2) A registered garment house in Ludhiana (Punjab) sold three lots of garments to a dealer in Bhatinda (Punjab) for Rs1000000; Rs600000 and Rs500000. It also charged Rs10000 on each lot of transportation charges . But on the occasion of Diwali , a discount of 1% was given on each lot . If the rate of GST is 5%, Calculate
a) IGST
b) CGST
c) SGST
3) Saurav went to watch a new movie in a multiplex. He wanted to buy a movie ticket for Rs80, but it was not available. So, he bought a ticket for Rs120. If the GST for a ticket below Rs100 is 18%, and GST for a ticket above Rs100 is 28%, how much extra GST and extra amount did saurav pay for the ticket?
4) A dealer in Rohtak (Haryana) bought a gold ring from a manufacturer in Gurgaon (Haryana) for Rs800000. He sold this ring to a dealer to Nainital (Uttarakhand) for Rs95000. If the rate of GST is 3% find
a) the new GST payable at Rohtak
b) Input tax credit (ITC) for dealer in Nainital.
5) A retailer in Jaipur( Rajasthan) buys goods from a dealer in Alwar (Rajasthan) at a discount 20%. The retailer sales it to a customer in Jaipur at the printed price. If the printed price of the goods is Rs16000 and the GST rate is 8%, calculate :
a) the prince paid by the customer for the goods.
b) the CGST and SGST payable by the retailer in Jaipur to the government.
Answer
1) Rs56588.80 2) 0, Rs52725, Rs52725 3) Rs19.20, Rs59.20 4) Rs450, Rs2850 5) Rs17280, 128, 129
LONG ANSWER TYPE QUESTIONS
1) An e-learning company in Delhi sets the marked price of an e-book as Rs75000. It sells the e-book to a dealer in Patna (Bihar) at discount of 30%. The dealer in Patna raises the marked price of the e-book by 30% and then sells it to a dealer in Ranchi (Jharkhand). if the rate of GST is 5%, find the GST paid by the dealer in Patna to the government.
2) A manufacturer in Noida (UP) sold a cartoon of hair oil to a dealer in Rajpur (Chhattisgarh) for Rs22000. The dealer in Raipur sold it to a consumer in Bastar (Chhattisgarh) at a profit of Rs5000. If the rate of GST is 18%, find:
a) the net IGST , CGST and SGST payable by the dealer in Raipur.
b) the cost price of the hair oil for the customer.
3) A dealer in Jodhpur (Rajasthan) supplied floor tiles worth Rs1700000 to a dealer in Delhi and another worth Rs300000 to a dealer in Jaipur (Rajasthan). The total value of his receipt of tiles in interstate transactions was Rs1500000. If the rate of GST is 18%, calculate the net IGST , CGST and SGST payable by the dealer in Jodhpur.
4) A shopkeeper sells an item for Rs2150. For a customer, he reduced the price of the item in such a way that the customer has to pay only Rs2124 including GST. If the rate of GST is 18%. Calculate the amount of reduction allowed by the shopkeeper .
5) A fruit juice company in Allahabad (UP) sold fruit juice worth Rs16000 to a dealer in Hapur(UP). The whole lot of juice was then supplied to a dealer in Rudrapur (Uttarakhand) for Rs17500. If the rate of GST is 12%. Find :
a) the net GST payable at Hapur.
b) input Tax credit (ITC) for the dealer in Rudrapur.
6) Radheshyam is a dealer of footwear in Moradabad (UP). He purchase footwear worth Rs200000. He sold 50% of thess footwear to a dealer in Agra (UP) for Rs130000 and the rest of the stock remains in his godown. If the rate of GST is 5%, find the excess credit of CGST and SGST to be carried forward.
7) The marked price of a video camera Recording is Rs80000. A dealer in Delhi buys it from a dealer in Mumbai (Maharashtra) at discount of 20% on the marked price . The dealer then sells it to a customer in Rohtak (Haryana) at a discount of 10% on the marked price. if the rate of GST is 18%, calculate the amount of tax payable by the dealer in Delhi to the government.
Answer
1) Rs2250 2) Rs0, Rs0, Rs900, Rs31860 3) Rs36000, Rs27000, Rs27000 4) Rs350 5) Rs180, Rs2100 6) Rs750, Rs750 7) Rs1440
SHARES AND DIVIDEND
1) The total amount of money needed to run the company is called:
a) shares b) capital c) dividend d) principle
2) The whole capital to run a company is divided into small units, called:
a) Shares b) Share holders c) face value d) dividend
3) The annual profit distributed among share holders is called:
a) nominal value b) market value c) dividend d) face value
4) The value of a share printed on the share certificate is called its :
a) nominal value b) market value c) discount d) below par
5) The shares of different companies can the brought or sold in the market through stock exchange. The price at which the share is share or purchased is called its
a) face value b) market value c) par value d) Nominal value
6) A share is said to be____, if its market value is the same as its face value.
a) premium b) discount c) par c) nominal value
7) A share is said to be at premium, if its market value is ____then its face value.
a) more b) less c) same d) equal
8) A share is said to be____, if its market value is less than its face value.
a) At par b) above par c) below par d) premium
9) The face value of a share
a) change every year b) changes from time to time c) always remains the same d) none to
10) Dividend is always paid on the____ of a share.
a) market value b) face value c) investment d) dividend
11) The market value of a share.
a) never changes b) changes from time to time c) changes every month d) none
12) Number of share hold by a person=
a) total nominal value/face value of one share
b) total market value/ face value of one share.
c) dividend/market value of one share.
d) dividend/investment x 100
13) dividend =
a) number of shares x nominal value
b) number of shares x market value
c) face value x number of shares x rate of dividend/100
d) none
14) Rate of return on investment=
a) investment/dividend
b) dividend/investment
c) dividend/ investment x 100
d) investment/dividend x 100
15) investment/ sale proceeds =
a) number of shares x market value
b) number of shares x nominal value
c) face value x number of shares x rate of dividend
d) dividend/investment
16) annual income of a share holder
a) number of shares x face value
b) number of shares x rate of dividend x face value of 1 share
c) number of shares x market value x face value
d) market value x nominal value x 100
17) If a share of of Rs100 is selling at Rs125, then it is said to be selling at a ___ of Rs25.
a) discount b) premium c) at par d) below par
18) if a share of Rs125 is selling at Rs96, then it is said to be selling at Rs 29___.
a) below par b) at par c) above par d) premium
19) if Kabir invests Rs 10320 on Rs100 shares at a discount of Rs14, then the number of shares he buys is
a) 110 b) 121 c) 150 d) 100
20) Shahrukh has some shares of Rs50 of a company paying 15% dividend. If his annual income is Rs 3000, then the number of shares he processes is
a) 400 b) 600 c) 800 d) 200
21) If Kiran invests Rs19250 on Rs50 shares at a premium of 20%, then the number of shares she buys is
a) 640 b) 160 c) 320 d) 240
22) Varun possesses 600 shares of Rs25 of a company. If the company announces a dividend of 8%, then his annual income is
a) Rs600 b) Rs1200 c) Rs480 d) Rs120
23) A man invests Rs24000 on Rs60 shares at a discount of 20%. If the dividend declared by the company is 10%, then his annual income is
a) Rs2880 b) Rs1500 c) Rs3000 d) none
24) Rs25 shares of a company are selling at Rs20. If the company is playing a dividend of 12%, then the rate of return is
a) 10% b) 18% c) 15% d) 12%
25) Rs 40 shares of a company are selling at 25% premium. If Mr Washim wants to buy 280 shares of the company, then the investment required by him is
a) Rs14000 b) Rs16800 c) Rs8400 d) Rs10000
1b 2a 3c 4a 5b 6c 7a 8c 9c 10b 11b 12a 13c 14c 15a 16b 17b 18a 19b 20a 21c 22b 23c 24c 25a
SHORT ANSWERS:
1) Find the % return on investment in
a) 6% Rs100 shares at Rs120
b) 25/3% Rs100 share at Rs150
2) Find the price of 5% Rs100 shares when an investor gets a dividend of Rs65 by investing Rs1430.
3) At what price should a 25/4% Rs 100 shares be quoted when the money is worth 5%
4) A person invested Rs1284 in 8/2% Rs100 shares . His dividend was Rs54. Calculate the M.V of the shares.
5) A company pays 7% dividend . For how much should a man buy a Rs100 shares for getting 8% on his investment.
6) Which share is more profitable: 4% Rs100 share at Rs80 or 9/2% Rs100 share at Rs88 ?
7) A part of Rs3020 is invested in 6% Rs100 shares at Rs97 and the rest in 12% Rs100 share at Rs108. If both bring the same dividend, find the sum invested in the share selling
a) at discount
b) above par
c) the total dividend
8) A person bought 360 ten rupee share paying 12% dividend at par and sold them at Rs21. The proceeds were invested in 5 rupees shares paying 9/2% at 3.5 per share. Find
a) sale proceeds
b) the number of 5 rupees shares bought
c) the percentage in income
9) A person invests Rs4368 in 100 rupees share at Rs91. Shares worth Rs24000 face value are sold at Rs95 and the rest at Rs85. Find
a) the number of shares bought Rs91
b) the number of shares sold at Rs85
c) the loss or gain in the deal .
10) Rs8000 and Rs 10000 were invested in Rs100 shares giving dividends 12% and 8% respectively. The dividend are collected and all the shares are sold at a loss of 2% and 3% respectively on the investment. Find
a) the dividend collected
b) the total sell proceeds
c) gain percent on the whole transaction.
1) 5%, 50/9% 2)Rs110 3) Rs125 4) Rs107 5) Rs87.50 6) 9/2 shares at Rs88 7) Rs1940, Rs1080, Rs240 8) Rs 7560, Rs 2160, 12.5% 9) 48,24, Rs 48 loss 10) Rs 1760, Rs 17540, 65/9%
LONG ANSWER
1) A man has a choice to invest in Rs 100 shares of two firms at Rs120 each or at Rs132 each. The first firm pays a dividend at 5% per annum and the second firms pays a dividend of 6% per annum. How much more will his annual return be if he invests Rs 26400 with the firm from which he gets a better return on his investment ?
2) A man bought one thousand shares each of face value Rs5 at Rs7 per share . At the end of the year, the company from which he bought the shares declared a dividend of 8%. Calculate
a) the amount of money invested by the man
b) the percentage return on his outlay. (Correct to one decimal place).
3) Ajay owns 560 share of a company. The face value of each share is Rs25. The company declares a dividend of 9%. Calculate
a) the dividend that Ajay will get.
b) the rate of interest on his is investment, if Ajay had to pay Rs30 for each share.
4) A company with 4000 shares of nominal value of Rs110 each declares an annual dividend of 15%. Calculate
a) the total amount of dividend paid by the company.
b) the annual income of shah Rukh who holds 88 shares of the company.
c) If he received only 10% on his investment, find the price Shah Rukh paid for each share.
5) Amit Kumar invests Rs36000 in buying Rs100 shares at Rs20 premium. The dividend is 15 percent per annum. Find
a) the number of shares he buys .
b) his yearly dividend
c) the percentage return on his investment
6) Vivek invested Rs45000 in 8% Rs10 shares at Rs15 sells the shares when the price rise to Rs30 and invests the proceeds in 12% Rs100 shares at Rs125. Calculate
a) the sale proceeds
b) the number of Rs125 shares he buys
c) the change in his annual income from dividend.
1) Rs 100 2) Rs 7000, 5.7% 3) Rs 1260, 7.5% 4) Rs 66000, Rs 1452, Rs 165 5) 300, 4500,12.5% 6) Rs 9000,72, Rs 624
SECTION AND MIDPOINT FORMULA
1) The centroid of the triangle whose vertices are (3,7),(-8,6) and (5,10) is
a) (0,9) b) (0,3) c) (1,3) d) (3,3)
2) A line interestc the y-axis and x-axis at the points A and B respectively. If (2,-5) is the midpoint of AB, then the coordinates of A and B are, respectively :
a) (0,-5) and (2,0) b) (0,10) and (-4,0) c) (0,4) and (-10,0) d) (0,-10) and (4,0)
3) If O (a/3,4) is the midpoint of a line segment joining the point X(-6,5) and Y(-2,3), then the value of a is
a) -4 b) -6 c) 12 d) -12
4) If the centroid of the Triangle formed by (7,x),( y,- 6) and (9,10) is (6,3), then the values of x and y respectively are:
a)( 5,3) b) ( 5,2) c) (-3,2) d) (6,5)
5) The ratio in which the point (3/4, 5/12) divides the line segment joining the point A(1/2, 3/2) and (2,-5) is
a) 1:2 b) 3 : 2 c) 1:5 d) 2 :3
6) The fourth vertex D of a parallelogram ABCD whose three vertices are A(-2,3), B(6,7) and C(8,3) is
a) (0,1) b) (0,-1) c) (-1,0) d) (1,0)
7) The ratio in which the point P(4, m) divides the line segment joining the points A(2,3) and B(6,-3) is
a) 1:2 b) 2:1 c) 1:3 d) 1:1
8) If A(m/2,5) is the midpoint of the line segment joining the points Q(-6,7) and R(-2,3), then the value of m is
a) -8 b) -4 c) 12 d) 6
9) The midpoint of the line segment joining the points(-5,7) and (-1,3) is
a) (-3,7) b) (- 3,5) c) (- 1,5) d) ( 5,-3)
a) (6,9) b) (7,9) c) (-7,9) d) (7,-9)
11) The ratio in which P(m,4) divides the line segment joining the points A(2,5) and B(6,-3) is
a) 1:2 b) 2: 1 c) 1:3 d) 1 :7
12) if the midpoint of the line segment joining the points P(6, b - 2) and Q(- 2,4) is (2,-3), then the value of b=
a) -5 b) -6 c) -7 d) - 8
13) If the coordinates of one end of a diameter of a circle are (2,3) and the coordinates of its centre are (-2,5), then the co-ordinates of the other end of the diameters are:
a) (-6,7) b) (6,-7) c) (6,7) d) (-6,-7)
14) The point which lies on the perpendicular bisector of the line segment joining the points A(-2,-5) and B(2,5) is
a) (0,0) b) (0,2) c) (2,0) d) (-2,0)
15) The vertices of a parallelogram in order are A(1,2), B(4, y), C(x, 6), D(3,6). The value of x and y respectively are:
a) 6, 2 b) 3, 6 c) 5, 6 d) 1,4
16) If A(1,3), B(-1,2), C(2,5) and D(x, y) are the vertices of a parallelogram ABCD, then the value of x is
a) 3 b) 4 c) 0 d) 3/2
1b 2d 3d 4b 5c 6a 7d 8a 9b 10b 11d 12d 13a 14a 15a 16b
SHORT ANSWER TYPE QUESTIONS
1) Find the ratio in which the line segment joining (-2,5) and (-5,-6) divided by the line y= -3. Hence find the point of intersection .
2) P(1,-2) is a point on the line segment joining A(3,-6) and B(x, y) such that AP: PB is equal to 2:3. Find the coordinates of B.
3) In what ratio is the line segment joining P(5,3) and Q(-5,3) divided the y-axis ? Also find the coordinanates of the point of intersection.
4) In what ratio does the point C(3/5,11/5) divide the line segment joining the points A(3,5) and B (-3,-2)?
5) Find the coordinanates of the point of trisection (i.e., points dividing into three equal parts) of the line segment joining the points A(2,-2) and B(-7,4).
6) Find the ratio in which the y-axis divides the line segment joining the points (5,-6) and (-1,-4). Also, find the point of intersection.
7) If the points A(6,1), B(8,2), C(9,4) and D(p,3) are the vertices of a parallelogram, taken in order, find the value of p.
8) In the figure, line APB meets the x-axis at A and y-axis at B. P is the point (-4,2) and AP: PB= 1:2. Write down coordinanates of A and B.
1) 8:3, (-46/11,-3)
2) (-2,4)
3) 1:1, (0,3) 4) 2:3 5) (-1,0),(-4,2)
6) 5:1, (0,-13/3)
7) 7
8) (-6,0),(0,6)
LONG ANSWER TYPE QUESTIONS
1) Find the ratio in which the point (-3, p) divides the line segment joining the points (-5,-4) and (-2,3). Hence, find the value of p.
2) If the co-ordinate the midpoints of the sides of a triangle are (1,2),(0,1) and (2,-1), find the coordinates of its vertices.
3) The base BC of an equilateral triangle ABC lies on y-axis. The co-ordinates of point C are (0,-3). If the origin is the mid point of the base BC, find the coordinates of the points A and B.
4) P and Q are the points on the line segment joining the points A(3,-1) and B(-6,5) such that AP= PQ= QB. Find the co-ordinates of P and Q.
5) Find the lengths of the median of a triangle whose vertices are A(7,-3), B(5,3) and C(3,-1).
6) The line segment joining P(-4,5) and Q(3,2) intersects the y-axis at R. PM and QN are perpendicular from P and Q on x-axis. Find
a) the ratio PR: RQ.
b) the co-ordinates of R.
c) the area of the quadrilateral PMNQ
7) The line segment joining the points (3,-4), and (1,2) is trisected at the points P and Q. If the coordinates of P and Q are (p, -2) and (5/3, q) respectively, find the value of p and q.
1) 2:1, 1,2/3
2) (1,-4),(3,2),(-1,2)
3) (0,3),(±3√3,0)
4) (0,1),(-3,3)
5) 5 units, 5 units, √10 units
6) 4:3, (0,23/7), 24.5 sq units
7) 7/3,0
MEASURE OF CENTRAL (MEAN)
1) If the classes of a frequency distribution are 0-10, 10-20, 20-30,....50-60, then the size of each class is
a) 9 b) 10 c) 11 d) 5.5
2) The measure of central tendency of a statistical data which takes into account all the data is :
a) mean b) median c) mode d) range
3) For a group frequency distribution, we use bar X = ∑fx/∑f, here x stands for :
a) width of a class
b) lower limit of a class
c) class mark of a class d) none
4) For a grouped frequency distribution, we use bar X = A+ ∑fd/∑f to find the mean using shortcut method: here d stands for
a) width a class
b) midpoint of a class
c) frequency of a class
d) deviation of class mark from assumed mean .
5) For a grouped frequency distribution, we use bar X = A + ∑ft/∑f Here ∑f stands for:
a) sum of frequencies
b) Sum of class-marks
c) sum of upper limits of the classes.
d) sum of lower limits of the classes.
6) For a grouped frequency distribution we used bar X = A + ∑ft/∑f to find the mean using step deviation method. Here t is given by:
a) x - A B) (x+ A)/h c) (x - A)/h d) xA/h
7) While computing mean of a grouped data we assume that the frequency are:
a) evenly distributed over the classes
b) centred at the class marks of the classes
c) centred at the upper limits of the classes.
d) Centred at the lower limits of the classes.
8) If xᵢ's are the midpoints of the class intervals of grouped fᵢ's are corresponding frequencies and bar X is the mean, then ∑(fᵢxᵢ - bar X) is equal to:
a) 0 b) 1 c) -1 d) 2
9) The mean of the following frequency distribution to the nearest integer is
Class: 0-2 2-4 4-6 6-8
F: 2 1 4 3
a) 4 b) 5 c) 6 d) 7
10) The mean of the following distribution is
Clar: 1-3 4-6 7-9 10-12
F: 5 2 1 4
a) 10 b) 8 c) 6 d) 5
1b 2a 3c 4d 5a 6c 7b 8a 9b 10c
Short Answer Type Questions
1) Find the mean of the following data:
C-I: 0-10 10-20 20-30 30-40 40-50
F: 12 16 6 7 9 22
2) Find the mean of the following data using direct method:
C-I: 0-4 5-9 10-14 15-19
F: 2 8 7 3 9.75
3) Find the mean of the following data using short cut method:
C-I: 0-20 20-40 40-60 60-80
F: 10 8 15 7 39.5
4) Find the mean of the following data using step deviation method:
C-I: 1-3 3-5 5-7 7-9 8-11
F: 7 8 2 2 1 4.2
5) Find the mean of the following distribution:
Marks no of students
Less than 20 4
Less than 40 16
Less than 60 24
Less than 80 30 40.66
6) Find the mean of the following data:
Height (in cm) no of plants
More than 10 50
More than 20 36
More than 30 18
More than 40 5 26.8
7) If the mean of the following distribution is 22, then find the value of f:
Class 0-10 10-20 20-30 30-40 40-50
F: 12 16 6 f 9 7
8) The daily incomes of a group of 10 labourers are tabulated as below. Find the mean daily income of the labourers.
Income(in Rs) no of labourers
100-200 2
200-300 4
300-400 3
400-500 1 Rs280
Long Answer Type Questions
1) The mean of the following frequency distribution is 62.8 and the sum of all frequencies is 50. Compute the missing frequencies a and b.
Class Frequency
00-20 5
20-40 a
40-60 10
60-80 b
80-100 7
100-120 8
Total 50 8,12
2) The daily expenditure of 100 families is given below. Calculate x and y, if the mean daily expenditure is Rs188.
Expenditure(in Rs) no of families
140-160 5
160-180 25
180-200 x
200-220 y
220-240 5 50,15
3) Using the assumed mean method, find the mean of the following data:
Class: 0-10 10-20 20-30 30-40 40-50
F: 7 8 12 13 10 27.2
4) The following table gives the wages (in Rs) of workers (per day) in a factory:
Wages No of workers
130-134 5
134-138 8
138-142 14
142-146 12
146-150 11
Calculate the mean wage of the workers of the factory by using assumed -mean method (short cut) method. Rs 141.28
5) Calculate the mean of the following frequency distribution, using the step deviation method.
Class frequency
00-50 17
50-100 35
100-150 43
150-200 40
200-250 21
250-300 24 148.61
6) By using step deviation method, compute the arithmatic mean for the following data:
a) Marks. no of students
Less than 10 14
Less than 20 22
Less than 30 37
Less than 40 58
Less than 50 67
Less than 60 75 28.6
7) By using step deviation method, find the mean marks obtained by a student from the following data:
Marks. No of students
0 and above 80
10 and above 77
20 and above 72
30 and above. 65
40 and above 55
50 and above 43
60 and above 28
70 and above 16
80 and above 10
90 and above 8
100 and above 0 51.75
Median, Quartiles and Mode
1) From histogram, we can estimate.
a) mean of the data
b) median of the data
c) mode of the data
d) upper quartile of the data
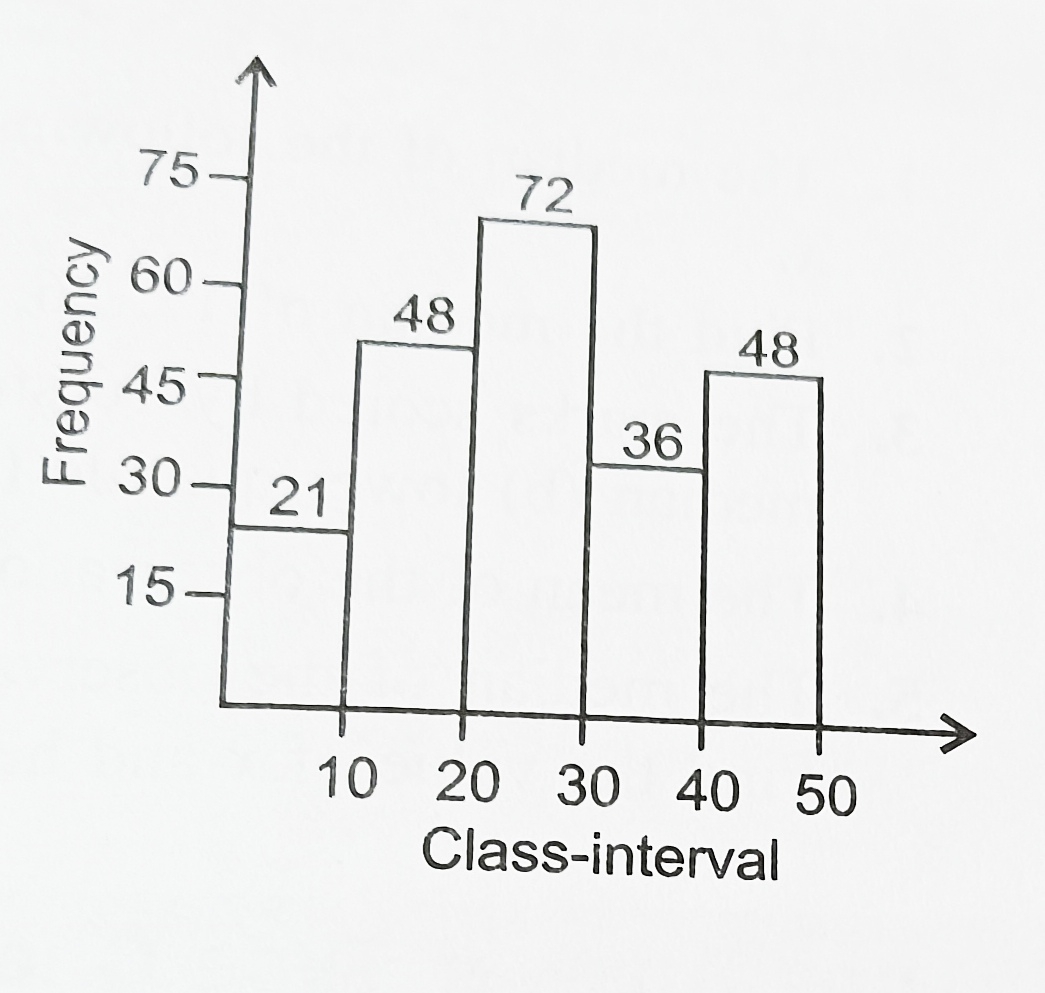
a) 72 b) 21 c) 48 d) 36
3) Which of the following is correct?
a) mode= 3 median - 2 mean
b) mode= 2 median - 3 mean
c) mode= 3 median + 2 mean
d) mode= 2 mean - 3 median
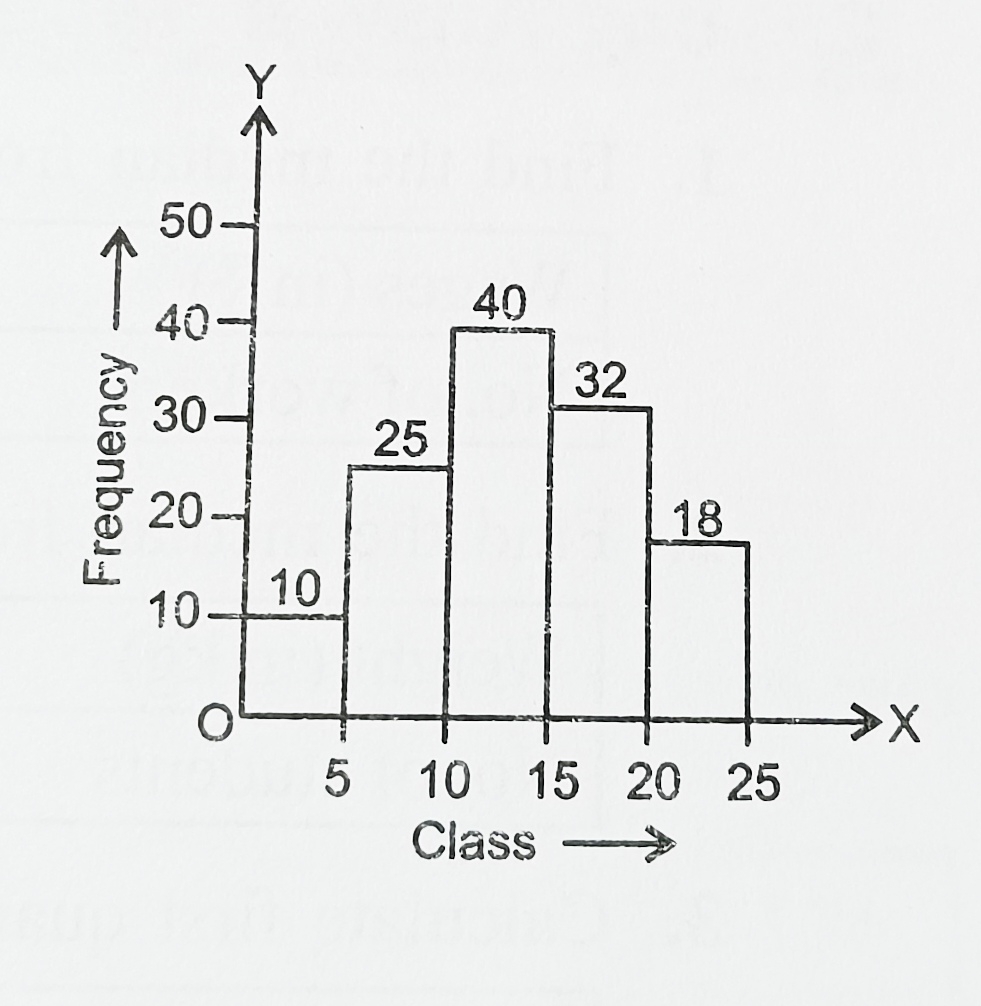
a) 10 b) 15 c) 20 d) 25
5) The class mark of the median class of the given distribution is
Class Cumulative frequency
00-10 8
10-20 10
20-30 17
30-40 26
40-50 30
a) 15 b) 25 c) 30 d) 35
6) Semi-inter quartile range is given by
a) (Q₃ + Q₁)/2
b) (Q₃ - Q₁)/2
c) (Q₃ + Q₁)
d) (Q₃ + Q₁)/3
7) The median of the data 8,5,-2,4,0,7,10,6,3 is
a) 0 b) 5 c) -2 d) 10
8) The mode of the given observation 10,22,15,18,17,15,10,21,9,6,10,16,15,4,15 is
a) 15 b) 10 c) 22 d) 6
9) From the data 37,35,30,34, 40,39,38,36 if 35 is removed, the median increases by:
a) 0.5 b) 1 c) 2 d) 35
10) The median of the data 78,56,22,34,45,54,39,68,54,84 is
a) 53 b) 54 c) 55 d) 56
11) In a grouped frequency distribution, the class with maximum frequency is called
a) mean class b) media class c) modal class d) quartile class
12) Quartile divide the whole set of observation into ____ equal parts.
a) two b) three c) four d) ten
13) The middle Quartile is also known as
a) median b) mode c) mean d) class mark
14) The difference between upper quartile (Q₃) and lower quartile ( Q₁) is called
a) range
b) semi inter quartile range
c) interquartile range d) limits
15) If the median of the data 24,25,26, x+2, x +3, 30,31,34 arranged in order is 27.5, then the value of x is
a) 25 b) 27 c) 28 d) 30
1c 2a 3a 4b 5d 6b 7b 8a 9a 10b 11c 12c 13a 14c 15a
Short Answer Type Questions
1) The median of the following obser11,12,14,18, (x +4), 30, 32,35,41 arranged in ascending order is 24. Find x.
2) Find the median of 17,26,60,45,33,32,29,34,56. If 26 is replaced by 62, find the new median.
3) The marks scored by 16 students in a class test are: 3,6,8,13,15,5 , 21,23,17,10, 9, 1,20,21, 18,12. Find
a) the median
b) lower quartile
c) upper quartile
4) The mean of the observations 23, (x -5),36, (x -9), (x -1) and 28 is 21. Find the value of x and hence find the median.
5) The median of the observation 11,12,14, (x -2), (x +4), (x +9),32,38 and 47 arranged in ascending order is 24. Find the value of x and hence find the mean,
1) 20 2) 33;34 3) 12.5,6,18 4) 18,20 5) 20,25
Long Answer Type Questions
1) Find the median from the following frequency distribution:
Wages. No of workers
280 12
320 16
360 20
440 17
480 13
550 11
2) Find the median from the following frequency distribution:
Weight no of students
56 6
59 8
62 13
64 12
66 9
70 6
3) Calculate first quartile, third quartile and quartile range from the following data:
Weight: 4 5 6 8 11 13 14
F: 2 4 5 7 3 2 1
4) In a class of 40 students, marks obtained by the students in a class test(out of 10) are given below:
Marks no of students
1 1
2 2
3 3
4 3
5 6
6 10
7 5
8 4
9 3
10 3
Calculate the following for the given distribution:
a) median
b) mode
5) The distribution given below shows the marks obtained by 25 students in an aptitude test. Find the median and mode of the distribution.
Marks: 5 6 7 8 9 10
F: 3 9 6 4 2 1
6) A mathematical aptitude test of 50 students was recorded as follows:
Marks no of students
50-60 4
60-70 8
70-80 14
80-90 19
90-100 5
Draw a histogram for the above data using a graph paper and locate the mode.
7) Draw a histogram for the following frequency distribution and find mode from the graph.
Class frequency
00-05 2
05-10 5
10-15 18
15-20 14
20-25 8
25-30 5
8) (Use a graph paper for this question.) The daily pocket expenses of 200 students in a school are given below:
Expenses. Frequency
00-05 10
05-10 14
10-15 28
15-20 42
20-25 50
25-30 30
30-35 14
35-40 12
Draw a histogram representing the above distribution and estimate the mode from the graph.
1) Rs360 2) 63kg 3) 5,8,3 lbs
4) 6,6
5) 7,6
6) 82.5 7) 14 8) 21
Long Answer Type Questions - II
1) The table shows the distribution of the scores obtained by 160 shooters in a shooting competition. Use a graph sheet and draw an ogive for the distribution. (take 2cm= 10 score on the x-axis and 2cm = 20 shooters on the y-axis).
Scores no of shooters
00-10 9
10-20 13
20-30 20
30-40 26
40-50 30
50-60 22
60-70 15
70-80 10
80-90 8
90-100 7
Use your graph to estimate the following:
a) the medium
b) the interquartile range
c) The number of shooters who obtained a score of more than 85%.
2) The daily wages of 80 workers in a project are given below:
Wages No of workers
400-450 2
450-500 6
500-550 12
550-600 18
600-650 24
650-700 13
700-750 5
Use a graph paper to draw an ogive for the above distribution. (Use a scale of 2cm = Rs50 on x-axis and 2cm = 10 workers on y-axis). Use your ogive to estimate:
a) the median wage of the workers.
b) the lower quartile wage of workers.
c) the number of workers who earn more than Rs625 daily.
3) Use graph paper for this question.
A survey regarding height (in cm) of 60 boys belonging to class 10 of a school was conducted. The following data was recorded:
Height no of boys
135-140 4
140-145 8
145-150 20
150-155 14
155-160 7
160-165 6
165-170 1
Taking 2cm = height of 10cm along one axis and 2cm= 10 boys along the other axis, draw an ogive for the above distribution. Use the graph to estimate the following:
a) the median
b) lower quartile
c) if above 158cm is considered as the tall boys of the class, find the number of boys in the class who are tall.
4) 40 students enter for a game of shot-put competition. The distance thrown (in metres) is recorded below:
Distance no of students
12-13 3
13-14 9
14-15 12
15-16 9
16-17 4
17-18 2
18-19 1
Use a graph paper to draw an ogive for the above distribution.
Use a scale of 2cm= 1m on one axis and 2cm = 5 students on the other axis.
Hence using your graph find
a) the median
b) upper quartile
c) the number of students who cover a distance which is above 33/2 m.
1) 44 31 11
2) Rs600, Rs 550, 29
3) 149cm, 146, 9
4) 14.6m, 15.6m, 5
BANKING
1) Sujata has a recurring deposit account in a bank for 2 years at 6% p.a, simple interest. If she gets Rs1200 as interest at the time of maturity, then her monthly installment is :
a) Rs500 b) Rs600 c) Rs700 d) Rs800
2) A man deposited Rs1000 per month in a recurring deposit account for 3 years at 8% p.a, The maturity value is:
a) Rs440000 b) Rs 40000 c) Rs40440 d) Rs44444
3) Abhinav deposited Rs200 per month for 3 years in a bank's recurring deposit account. If the bank pays intrest at the rate of 11% p.a., then the interest at the time of maturity is:
a) Rs1210 b) Rs1221 c) Rs1415 d) Rs1521
4) Kamal has a recurring deposit account in a bank for 2 years at 6% p.a., S. I. if he gets Rs1350 as interest, then the monthly installment is:
a) Rs1000 b) Rs900 c) Rs850 d) Rs
5) if Kavita deposited Rs900 per month for 2 years and 6 months in a recurring deposit account, then the total money she deposited in the account is:
a) Rs 26000 b) Rs27000 c) Rs28000 d) Rs30000
6) A man deposited RsX per month for Y years in a recurring deposit account. If at the time a maturity he got RsZ as interest, then the total maturity amount is:
a) Rs(12XY + Z) b) Rs 12 X Y Z c) Rs( X Y + 12Z) d) Rs XYZ/12
7) Karan deposited Rs2000 per month for 3 years in a recurring deposit account . if the rate of interest is 11% p.a., the amount he gets on maturity is:
a) Rs72000 b) Rs80000 c) Rs82210 d) Rs 84210
8) A man deposited Rs2000 per month in a recurring deposit account for 18 months at 8% p.a, The interest he will get at the time of maturity is :
a) Rs2280 b) Rs2350 c) Rs2400 d) Rs2410
9) Mr Awasthi has a 4 year time deposit account and deposits Rs 650 per month. If he received Rs5096, as interest at the time of maturity, the rate of interest is:
a) 8% p.a b) 8.5%p.a c) 9%p.a d) 10%p.a
10) Sharda deposited Rs150 per month in a bank for 8 months under the recurring deposit scheme. If the rate of interest is 8% p.a., then intrest earned at the time of maturity is:
a) Rs50 b) Rs40 c) Rs36 d) Rs30
11) Ravi has a 4 year cumulative time deposit account and deposits Rs650 per month. If he receives Rs36296 at the time of maturity , the rate of interest was :
a) 10% p.a b) 9%p.a c) 8%p.a d) 7.5%p.a
12) Piyush has a recurring deposit account for 2 years at 10%p.a. If he receives Rs1900 as intrest , the monthly installment paid by him is:
a) Rs700 b) Rs750 c) Rs760 d) Rs800
13) A man deposited Rs1500 every month in a bank for 8 months under the recurring deposit scheme. If the rate of interest is 8%p.a, than the interest earned at the time of maturity is:
a)Rs 400 b) Rs350 c) Rs36⁰ d) Rs320
14) Kamal deposits Rs4000 per month in a recurring deposit account for 3/2 years at 6%p.a. The intrest he will receive at the time of maturity is:
a)Rs 3420 b) Rs3240 c) Rs3150 d) Rs3110
15) Garima deposited Rs500 per month in a recurring deposit account for 3 years. If the rate of interest is 4%p.a, then the amount she gets at the time in maturity is:
a) Rs1110 b) Rs19110 c) Rs 20150 d) Rs21110
16) Amrita deposited Rs1600 per months in a recurring deposit account for 2 years. If the rate of interest is 8% p.a, then the interest earned by her at the time of maturity is:
a) Rs 3200 b) Rs3450 c) Rs3550 d) Rs3600
17) Manisha deposited Rs500 per month recurring deposit account for 2 years. If the bank pays interest at 8%p.a, then the interest she gets at the time of maturity is:
a) Rs 1000 b) Rs1100 c) Rs 1200 d) Rs1500
18) Ajay deposited Rs2400 per month for 18 months in a bank's recurring deposit account. If the bank pays interest at 6%p.a, the interest he gates at the time of maturity is:
a) Rs 1550 b) Rs18000 c) Rs2052 d) Rs3250
19) Sameer has a recurring deposit account in the bank for 3 years at 4% simple interest. If he gets Rs4440 as interest at the time of maturity, then the monthly installment is:
a) Rs2000 b) Rs26000 c) Rs3000 d) Rs3200
20) Dinesh has a recurring deposit account, which pays interest at 5%p.a. if he pays Rs 2500 per month for 2 years, then the interest he will get at the time and maturity is
a) Rs 3000 b) Rs3025 c) 3200 d) Rs3125
1d 2c 3b 4b 5b 6a 7d 8a 9a 10c 11c 12c 13c 14a 15b 16a 17a 18c 19a 20d
Short Answer Type Questions:
1) Rekha opened a recurring deposit account for 20 months. The rate of interest is 9% per annum and Rekha receives Rs441 as interest at the time of maturity. Find the amount Rekha deposited each month.
2) Mr Sonu has a recurring deposit account and deposited Rs750 per month for 2 years. If he gets Rs19125 at the time of maturity, find the rate of interest.
3) Kabeer opened a recurring deposit account in a bank and deposited Rs300 per month for 2 years. If he received Rs7725 at the time of maturity, find the rate of interest per annum.
4) Ram deposits Rs1000 per month in a recurring deposit account for 3 years at 8% per annum intrest. Find the maturity value.
5) Reema deposited Rs200 per month for 3 years in a bank' recurring deposit account. If the bank pays interest at the rate of 11% p.a., find the amount she gets on maturity.
6) Harishankar opened a recurring deposit account in a bank and deposited Rs800 per month for 18 month. If he received Rs15084 at the time of maturity, find the rate of interest per annum.
Answers
1) Rs280 2) 6% 3) 7% 4) Rs40440 5) Rs8421 6) 6%
Long Answer Type Questions
1) Mohan has a recurring account in a bank for 2 years at 6% simple interest. If he gets Rs1200 as intrest at the time of maturity, find
a) the monthly installment.
b) the amount of maturity.
2) Priyanka has a recurring deposit account of Rs1000 per month at 10% per month. If she gets Rs5550 as interest at the time of maturity, find the total for which the account was held.
3) Manish opened a recurring deposit account in a bank. He deposited per month for two years. At the time of maturity, he got Rs67500. Find
a) the total interest earned by Manish.
b) the rate of interest per annum.
4) Mr Gupta has a recurring deposit account in a bank. He deposits Rs2500 per month for 2 years. If he gets Rs66250 at the time of maturity, find
a) the interest paid by the bank.
b) the rate of interest.
5) Mr Garg deposits a certain sum of money each month in a recurring deposit account of a bank. If the rate of interest is 8% p.a and Mrs Garg gets Rs 8088 from the bank after 36 months, find the value of his monthly installment.
5) Vandana has recurring time deposit account of Rs340 per month at 6% p.a. If she gets Rs7157 at the time of maturity, find the total time for which the account was held.
Answers:
1) Rs8000, Rs20400 2) 3 years 3) Rs7500, 12% 4) Rs6250, 10% 5) Rs200 6) 20 months
TRIGONOMETRIC IDENTITIES
1) {(1+ tanθ)/(1+ tanθ)}² =
a) 1 b) tan²θ c) tanθ d) 4
2) (sinA - 2 sin³A)/(2cos³A - cosA) is equal to
a) secA b) tanA c) cotA d) 1
3) If tanx = cotx, then
a) x - = 90 b) x= y = 90 c) x + y= 90 d) y - x =90
4) (sec²θ -1)(1- cosec²θ) is equal to
a) -1 b) cotθ c) 0 d) cosecθ
5) √{(secθ -1)/(secθ +1)} + √{(secθ +1)/(secθ -1)} is equal to
a) 2cosecθ b) 2secθ c) 2tanθ d) 2sinθ
6) If sinθ + cosθ = a and secθ + cocosθ =b, then the value of b(a²-1) is
a) 2a b) a+ b c) 2b d) a - b
7) If sinθ + cosθ = √2cosθ, then the value of cosθ - sinθ is
a) √cosθ b) sinθ c) √sinθ d) cosθ
8) cosec²θ/(1 + cot²θ) =
a) 0 b) cosec θ c) 1 d) cotθ
9) sinθ + 2cosθ = 1, then the value of 2sinθ - cosθ =
a) 1 b) 2 c) √2 d) 0
10) If (sinθ + cosθ)(tanθ + cotθ) =
a) secθ + tanθ b) secθ c) secθ + coseθ d) cosecθ
11) sinθ/(1+ cosθ) + (1+ cosθ)/sinθ =
a) 2sinθ b) 2cosθ c) 2tanθ d) 2cosecθ
12) cosθ/(1- sinθ) + cosθ/(1+ sinθ) =
a) 2sinθ b) 2cosθ c) 2 cosecθ d) 2secθ
13) 5 tan²θ - 5 se²θ =
a) 5 b) -5 c) 1/5 d) 0
14) If secθ + tanθ =p, then (p²-1)/(p²+1)=
a) tanθ b) cosθ c) sinθ d) cocosθ
15) sin⁶θ + cos⁶θ + 3sin²θ. cos²θ =
a) 0 b) 1 c) 2 d) -2
16) If sinθ + cosθ = √3, then tanθ + cotθ =
a) 1 b) -1 c) 2 d) -2
17) secθ(1- sinθ)(secθ + tanθ) =
a) 0 b) 1/2 c) 1 d) none
18) 9 sec²θ - 9 tan²θ =
a) 1 b) 9 c) 8 d) 0
19) (1+ tanθ + secθ)(1+ cotθ - cosecθ =
a) 0 b) 1 c) 2 d) -1
20) (1+ tan²θ)/(1+ + cot²θ) =
a) sec²θ b) -1 c) cot²θ d) tan²θ
21) (secθ + tanθ)(1- sinθ =
a) secθ b) sinθ c) cocosθ d) cosθ
22) 2 cos²θ + 2/(1+ cot²θ) =
a) 1 b) 2 c) 0 d) 1/2
23) Simplified form of (3- tanθ)/(3cosecθ - secθ) is
a) cosθ b) sinθ c) cocosθ d) tanθ
1b 2b 3c 4a 5a 6a 7c 8c 9b 10c 11d 12d 13b 14c 15b 16a 17c 18b 19c 20d 21d 22b 23b
SHORT ANSWER TYPE QUESTIONS
Prove the following:
1) secθ/(secθ -1) + secθ/(secθ + 1) = 2cosec²θ.
2) √(sec²θ + cosec²θ) = tanθ + cotθ
3) (cosecθ - sinθ)(secθ - cosθ)(tanθ + cotθ) = 1
4) sinθ/(1+ + cotθ) - cosθ/(1+ tanθ) = sinθ - cosθ
5) sin⁴θ - cos⁴θ = 1- 2cos²θ
6) (1- sinθ)/(1+ sinθ) = (secθ - tanθ)²
7) (sin²x cos²y - cos²x sin²y) = sin²x sin²y.
8) Simplify: (sec²θ - 2 tan²θ)(1- sinθ)(1+ sinθ).
9) For what value of x, 2sin²x - cos²x = 2 ?
10) Find the value: tan²x + cot²x - sec²x cosec²x.
11) sinθ/(cotθ + cosecθ) - sinθ/(cotθ - cosecθ).
8) 1- 2 sin²θ 9) 90° 10) -2 11) 2
LONG ANSWER TYPE QUESTIONS
1) If tanθ + sinθ =m and tanθ - sinθ =n, show that m²- n²= 4 √(mn).
2) Show that: (secθ + tanθ -1)/(tanθ - secθ +1) =(1+ sinθ)/cosθ.
3) If tanθ + secθ = m, then find the value of (m²+1)/2m.
4) Express, a cosθ - b sinθ in terms of a, b and c, where a sinθ + b cosθ = c.
5) Show that: tanθ/(1- cotθ) + cotθ/(1 - tanθ) = tanθ + cotθ+ 1.
6) Show that: (secθ + tanθ -1)(secθ - tanθ +1)/tanθ = 2.
7) If x= a secθ + b tanθ and y= a tanθ + b secθ, then evaluate (a²- b²)/(x²- y²).
8) If x= a secm cos n, y= b secm sin n and z= c tan m, then evaluate x²/a² + y²/b² - z²/c².
9) Show that: 1/(secθ - tanθ) - 1/cosθ - 1/(secθ + tanθ).
10) Show that (1+ cotθ - cosecθ)(1+ tanθ + secθ) = 2.
3) secθ 4) ± √(a²+ b² - c²)
BOOSTER - B
1) Solve the following equations by factorisation:
a) x² + 6x + 5=0. -5,-1
b) 8x² -22x -21 =0. 7/2,-3/4
c) 9x² - 3x -2 =0. 2/3,-1/3
2) Solve the following equations by factorisation method:
a) x² + 2√2x -6 =0. -3√2, √2
b) √3 x² + 10x + 7√3 =0. -√3, -7/√3
3) Solve the following equation by factorisation method:
a) x² - 9=0. ±3
b) x² - 8x + 16=0. 4,4
4) Solve the following equation by factorisation method:
a) x/(x +1) + (x +1)/x = 34/15, x≠0, x≠ -1. 3/2,-5/2
b) (x+3)/(x -2) - (1- x)/x = 17/4, 4,-2/9
c) 1/(x -2) + 2/(x -1) = 6/x. 3, 4/3
5) Solve the following equation by factorisation method:
a) 4/x - 3 = 5/(2x +3). -2, 1
b) 2x/(x -3) + 1/(2x +3) + (3x +9)/{(x -3)(2x +3) = 0. -1
6) x= 1/2- 1/2 - 1/(2- x), x ≠ 2. 1,1
7) Solve the following equation by factorisation method:
a) x²- 2ax + a²- b²= 0. a- b, a+ b
b) x²- 4ax + 4a²- b²= 0. 2a- b, 2a+ b
c) 4x²- 4ax + (a²- b²)= 0. (a+ b)/2, (a - b)/2
d) 4x²- 4a⅖x + (a⁴- b⁴) = 0. (a¹+ b²)/2, (a²- b²)/2
8) Solve the following equation by factorisation method:
a) 4x²- 2(a²+ b²)x + a²b²= 0. a²/2, b²/2
b) 9x²- 9(a+ b)x + (2a²+ 5ab + 2b²) = 0. (2a+ b)/3, (a+ 2b)/3
9) Solve the following equation by factorisation method
a) x²+ {a/(a+ b) + (a+ b)/a }x + 1= 0. -a/(a+ b), -(a+ b)/a
b) x² + x - (a+1)(a+ 2) = 0. -(a+2), a+1
c) x² + 2x - (a²+ a -2) = 0. -(a +2), a -1
10) Solve the following equation by factorisation method:
a) 1/(a+ b + x) = 1/a + 1/b + 1/x, a+ b ≠0. -a, - b
11) Solve:
a) x + 1/x = 25+ 1/25. 25, 1/25
b) (x -3)+x -4)= 34/33². 98/33, 133/33
BOOSTER - C
1) Write the discriminant of the following equations
a) x²- 4x +2=0. 8
b) 3x² + 2x - 1=0. 16
c) x²- 4x + a=0. 16- 4a
d) √3 x²- 2√2x - 2√3=0. 32
e) x² + x + 1 =0. -3
f) x² + px +2q =0. p¹- 8q
2) Determine the nature of the roots of the following equations:
a) 2x² + x -1 =0. Real, distinct
b) x²- 4x + 4=0. Real, equal
c) x² + x + 1=0. Not real
d) 4x²- 4x + 1 =0. Real, equal
e) 2x²+ 5x +5 =0. Not real
3) In the following, determine whether the given Equation have real roots and if so, find the roots.
a) 9x²+ 7x -2=0. Y, 2/9,-1
b) 2x²+ 5√3x +6 =0. Y, -√3/2,-2√3
c) 3x²+ 2√5x - 5=0. Y, √5/3,-√5
d) x²+ 5x + 5=0. Y, (-5±√5)/2
e) 6x²+ x -2 =0. Y, 1/2,-2/3
f) 25x²+ 20x +7 =0. N
4) Using Quadratic formula solve the following equation:
a) p²x²+ (p²- q²)x - q² =0. q²/p²,-1
b) 9x² - 9(a+ b)x + (2a²+ 5ab + 2b²) =0. (2a+ b)/3,(a+ 2b)/3
BOOSTER - D
1) Find the values of k for which the given Equation has real and equal roots:
a) 2x² - 10x + k =0. 25/2
b) 9x²+ 3kx + 4 =0. ±4
c) 12x²+ 4kx +3 =0. ±3
d) 2x²+ 7p3x + k =0. 9/8
e) 2x² - kx + 1=0. ±2√2
f) kx² - 5x + k =0. ±5/2
g) x²+ k(4x+ k -1) +2 =0. 2/3,-1
h) x² - 2x(1+ 3k)+ 7(3 +2k) =0. 2, -10/9
i) (k+1)x² - 2(k -1)x +1 =0. 0,3
2) Find the values of k for which the following equation has equal roots:
(k -12)x²+ 2(k -12)x +2=0. 12,14
3) If -4 is a root of the equation x²+ px - 4 =0 and the Quadratic equation x²+ px + k =0 has equal roots, find the value of k. 9/4
4) Find the values of k for which the equation x²- 4x + k =0 has distinct real roots. <4
5) Show that the equation x²+ ax - 4 =0 has real and distinct roots for all real values of a.
6) If p,q,r are real and p≠ q, then show that the roots of the quadratic equation (p - q)x²+ 5(p + q)x -2(p - q)=0 are real and unequal.
7) Determine the positive of k for which the equation x²+ kx + 64=0 and x² - 8x + k =0 will both have real roots. 16
8) Find the values of k for which the given Equation has real roots.
a) kx² - 6x -2=0. ≥ -9/2
b) 9x²+ 3kx + 4=0. ≤-4, ≥4
c) 5x² - kx + 1 =0. ≤-√20 or ≥ √20
9) Find the values of k for which the equation x²+ 5kx + 16 =0 has no real roots. -8/5< k < 8/5
10) If p,q,r and s are real numbers such that pr = 2(q+ s), then show that atleast one of the equation x²+ px + q=0 and x²+ rx + s =0 has real roots.
11) If the roots of the equation x²+ 2cx + ab =0 are real and unequal, show that the equation x² - 2(a + b)x + a²+ b²+ 2c²=0 has no real roots.
12) Show that the equation x²(a²+ b²)+ 2x(ac + bd) + (c²+ d²) =0 has no real root, if ad ≠ bc.
13) Find the value of k for which the given Equation has equal roots. Also, find the roots.
a) 9x² - 24x + k =0. 4/3
b) 2kx² - 40x +25 =0. 5/4
14) Find the value of k for which the equation (k +4)x²+ (k +1)x + 1 =0 has equal roots. 5,-3
15) If -5 is a root of the equation 2x²+ px - 15 =0 and the equation p(x²+ x)+ k =0 has equal roots, find the value of k. 7/4
16) Using quadratic formula, solve the following equation for x: abx²+ (b²- ac)x - bc =0. c/b, -b/a
17) Solve for x: (x -1)/(x +2) + (x -3)/(x - 4) = 10/3, x ≠ -2,4. (1±√297)/4
18) Solve for x: 1/(x -1) + 2/(x +2)=4/ (x +4), x≠ -1, -2, -4. 2±2√3
MEAN
BOOSTER - A
1) If the mean of 6,4,7, p and 10 is 8, find the value of p. 13
2) Find the sum of the deviation of the variate values 3,4,6,8,14 from the mean. 0
3) The mean of 40 observations was 160. It was detected on rechecking that the value of 165 was wrongly copied as 125 for computation of mean. Find the correct mean. 161
4) The mean of 100 items was found to be 30. If at the time of the calculation two items were wrongly taken as 32 and 12 instead of 23 and 11, find the correct mean. 29.9
5) The mean monthly salary of 10 members of a group is Rs1445, one more member whose monthly salary is Rs 1500 has joined the group. Find the mean monthly salary of 11 members of the group. Rs1450
6) the mean of 10 numbers is 20. If 5 is substracted from every number, what will be the new mean ? 15
7) The mean of 16 numbers is 8. if 2 is added to every number, what will be the new mean ? 10.
8) The mean of 5 numbers is 18. If one number is excluded, their mean is 16. Find excluded number. 26
9) If the mean of 5 observations x, x+2, x+4, x+6, x+8, is 11, find the mean of first three observations. 9.
10) The mean of 25 observation is 36. if the mean of first 13 observations is 32 and the mean of last 13 observatiorn is 39, find the 13th observation. 23
11) Find the mean of first n natural numbers. (n+1)/2
12) find the mean of 0, 2, 4, 6, 8,....2n. n
13) Find the mean of the first n odd natural numbers. n
14) if the mean of 1, 2, 3,....n is 6n/11, find the value of n. 11
15) The mean of a set of observation is K. If each observation is divided by p, p≠ 0 and then increased by 10, then show that the mean of the new set of observations is K/p + 10.
BOOSTER - B
1) Find the mean of the following distribution:
x: 4 6 9 10 15
f: 5 10 10 7 8 9
2) Following table shows the weights of 12 students:
Weight (in kgs): 67 70 72 73 75
No of students: 4 3 2 2 1
Find the mean weight. 70.25kg
3) Find the mean of the following distribution:
X: 10 30 50 70 89
F: 7 8 10 15 10. 55
4) If the mean of the following distribution is 6, find the value of p.
X: 2 4 6 10 p+5
F: 3 2 3 1 2 7
5) Find the value of p, if the mean of the following distribution is 7.5.
X: 3 5 7 9 11 13
F: 6 8 15 p 8 4 3
6) Find the missing frequencies in the following frequency distribution if it is known that the mean of the distribution is 1.46.
No of accidents(x): 0 1 2 3 4 5 total
Frequency (f): 46 ? ? 25 10 5 200 76,38
BOOSTER - C
1) The following table shows the weight of 12 students:
Weight (in kg): 67 70 72 73 75
No of students: 4 3 2 2 1
Find the mean weight. 70.25 kg
2) Find the mean wage from the data given below:
Wages: 800 820 860 900 920 980 1000
F: 7 14 19 25 20 10 5 891.2
3) Apply step-deviation method to find the AM of the distribution:
Variate (x) Frequency(f)
5 20
10 43
15 75
20 67
25 72
30 45
35 39
40 9
45 8
50 6 22.214
3) The weight in kilograms of 60 workers in a factory are given in the following frequency table. Find the mean weight of a worker.
Weight (in kg): 60. 61 62 63. 64 65
No of workers: 5 8 14 16 10 7 62.65
4) The table given the distribution of villages under different heights from sea level in a certain region. Compute the mean height of the region:
Height: 200 600 1000 1400 1800 2200
F: 142 265 560 271 89 16 984.51
BOOSTER - D
1) Find the mean of the following frequency distribution:
Class interval frequency
00-10 7
10-20 10
20-30 15
30-40 8
40-50 10 25.8
2) The following table gives the distribution of total household expenditure (in rupees) of manual workers in a city.
Expenditure (in Rs) frequency
100-150 24
150-200 40
200-250 33
250-300 28
300-350 30
350-400 22
400-450 16
450-500 7 266.25
3) A frequency distribution of the life times of 400 TV picture tubes tested in a tube company is given below. Find the average life of tube.
Life time(in hrs) no of tubes
300-399 14
400-499 46
500-599 58
600-699 76
700-799 68
800-899 62
900-999 48
1000-1099 22
1100-1199 6. 715hrs
4) The following table gives weekly wages in rupees of workers in a certain commercial organisation. The frequency of class 49-52 is missing. It is known that the mean of the frequency distribution is 47.2. find the missing frequency.
Weekly wages (Rs) no of workers
40-43 31
43-46 58
46-49 60
49-52 ?
52-55 27 44
5) The mean of the following frequency table is 50. But the frequencies a, and b in class 20-40 and 60-80 are missing. Find the missing frequencies.
Class frequency
00-20 17
20-40 a
40-60 32
60-80 b
80-100 19
Total. 120 28,24
6) Find the mean marks of students from the following cumulative frequency distribution:
Marks. No of students
0 and above 80
10 and above 77
20 and above 72
30 and above 65
40 and above 55
50 and above 43
60 and above 28
70 and above 16
80 and above 10
90 and above 8
100 and above 0 51.75
7) Find the mean marks of the students from the following cumulative frequency distribution:
Marks No of students
Below 10 5
Below 20 9
Below 30 17
Below 40 29
Below 50 45
Below 60 60
Below 70 70
Below 80 78
Below 90 83
Below 100 85 48.41
HEIGHT AND DISTANCE (1)
1) A tower stands vertically on the ground. From a point on the ground, 20 away from the foot of the tower, the angle of the elevation of the top of the tower is 60°. What is the height of the tower ? 20√3
2) The angle of elevation of a ladder leaning against a wall is 60° and the foot of the ladder is 9.5 m away from the wall. Find the length of the ladder. 19m
3) A ladder is placed along a wall of a house such that it's upper end is touching the top of the wall. The foot of the ladder is 2m away from the wall and the ladder is making an angle of 60° with the level of ground. Determine the height of the wall. 2√3m
4) An electric pole is 10m high. A steel wire tied to top of the pole is affixed at a point to the ground to keep the pole up right. if the wire makes an angle of 45° with the horizontal through the foot of the pole, find the length of the wire. 14.1m
5) A kite is flying at a height of 75 m from the ground level, attached to a string inclined at 60° to the horizontal. Find the length of the string to the nearest metre. 87m
7) A vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff . At a point on the plane 70m away from the tower, an observer notices that the angles of elevation of the top and the bottom of the flagstaff are respectively 60° and 45°. Find the height of the flagstaff and that of the tower. 51.24m, 70m
8) A vertically straight tree, 15m high , is broken by the wind in such a way that its top just touches the ground and make an angle of 60° with the ground. At what height from the ground did the tree break ? 6.9m
9) A vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height 5 m. At a point on the plane, the angles of elevation of the bottom and the top of the flagstaff are respectively 30° and 60°. Find the height of the tower. 2.5 m
10) A person observed the angle of elevation of the top of the tower as 30°. He walked 50m towards the foot of the tower along level ground and found the angle of elevation of the top of the tower as 60°. Find the height of the tower. 43.24 m
11) The shadow of the tower when the angle of elevation of the sun is 45° is found to be 10m longer than when it was 60°. Find the height of the tower. 23.66 m
12) A parachute is descending vertically and makes angles of the elevation 45° and 60° at two observing points to 100m apart from each other on the left side of himself. Find the minimum height from which he falls and the distance of the point where he falls on the ground from the just observation point. 236.6m, 136.6m
13) On the same side of a tower, two objects are located. When observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 150m, find the distance between the objects. 63.4m
14) The angle of elevation of a tower at a point is 45°. After going 40m towards the foot of the tower, the angle of elevation of the tower become 60°. Find the height of the tower. 94.64m
15) A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7m. From a point on the plane, the angle of elevation of the bottom of the flagstaff is 30° and that of the top of the flagstaff is 45°. Find the height of the tower. 9.56m
16) The length of the shadow of a tower standing on level plane is found to be 2x metres longer when the sun's attitude is 30° than when it was 45°. Prove that the height of the tower is x(√3 +1) metres.
17) A tree breaks due to the storms and the broken part bends so that the top of the tree touches the ground making an angle of 30° with the ground. The distance from the foot of the tree. 17.3m
18) A balloon is connected to a mateorological ground station by a cable of length 215m included at 60° to the horizontal. Determine the height of the baloon from the ground. Assume that that there is no slack in the cable. 186m
19) Two men on either of the cliff 80m high observes the angle of elevation of the top of the cliff to be 30° and 60° respectively. Find the distance between the two men. 184.8m
20) Two men standing on either side of a tower 60m high observe the angles of elevation of the top of the tower to be 45° and 60° respectively. Find the distance between the two men. 94.64m
21) Find the angle of elevation of the sun (sun's altitude) when the length of the shadow of a vertical pole is equal to its height. 45°
22) A fire in a building B is reported on telephone to two fire stations P and Q, 20 km apart from each other on a straight road. P observes that the fire is at an angle of 60° to the road and Q observes that it is at an angle of 45° to the road. Which station should send its team and how much will this team have to travel ? Station P, 14.64 km
23) A man on the deck of a ship is 10m above the water level. He observes that the angle of elevation the top of a cliff is 45° and the angle of depression of the base is 30°. Calculate the distance of the cliff from the ship and the height of the cliff . 10√3m, 27.32m
24) A man standing on the deck of a ship, which is 8m above water level. He observes the angle of elevation of the top of a hilly as 60° and the angle of the depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill. 8√3m, 32m
25) There are two temples, one on each bank of a river, just opposite to each other. One Temple is 50m high. From the top of this temple, The angles of depression of the top and the foot of the other temple are 30° and 60° respectively. Find the width of the river and the height of the other temple. 28.83m, 33.33m
26) The angle of the elevation of an aeroplane from a point on the ground is 45°. After a flight of 15 seconds, the elevation changes to 30°. if the aeroplane is flying at a height of 3000 m, find the speed of aeroplane. 527.04 kmph
27) An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds , its elevation is observed to be 30°. Find the speed of the aeroplane in kmph. 415.66 kmph
28) From the top of a 50m high tower, the angles of the depression of the top and bottom of a pole are observed to be 45° and 60° respectively. Find the height of the pole . 21.13m
29) The horizontal distance between two trees of different heights is 60m. The angle of depression of the top of the first tree when seen from the top of the second tree is 45°. If the height of the second tree is 80m, find the height of the first tree. 20m
30) A tree standing on a horizontal plane is leaning towards east. At 2 points situated at a and b exactly due west on it, the angles of elevation of the top are respectively α and β. Prove that the height of the top from the ground is {(b - a) tanα tanβ}/(tanα - tanβ). α β
31) The angle of elevation of the top of a vertical tower PQ from a point X on the ground is 60°. At a point 40 Y, 40m vertically above X, the angle of elevation of the top is 45°. Calculate the height of the tower. 94.64
33) If the angle of elevation of a cloud from a point h metres above a lake is α and the angle of depression of its reflection in the lake β, prove that the distance of the cloud from the point of observation is (2h secα)/(tanβ - tanα).
34) From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive mile stones on opposite sides of the aeroplane are observed to be α and β. Show that the height in miles of aeroplane above the road is given by (tanα tanβ)/(tanα + tanβ).
35) PQ is a post of given height a, and AB is a tower at some distance; α and β are the angles of elevation of B, the top of the tower, at P and Q respectively. Find the height of the tower and its distance from the post. a/(tanα - tanβ), (atanα)/(tanα - tanβ)
36) A ladder rests against a wall at an angle α to the horizontal. Its foot is pulled away from the wall through a distance a, so that it slides a distance b down the wall making an angle β with the horizontal. Show that a/b = (cosα - cosβ)/(sin β - sinα).
37) A tower subtends an angle α at a point A in the plane of its base and angle of depression of the foot of the tower at a point b metres just above A is β. Prove that the height of the tower is b tanα cotβ.
38) An observer 1.5m tall, is 28.5m away from a tower 30m high . Determine the angle of the elevation the top of the tower from his eye. 45°
39) A carpenter makes stools for electricians with a square top of side 0.5m and at a height of 1.5 m above the ground. Also , each leg is inclined at an angle 60° to the ground. Find the length of each leg and also the length of the two steps to be put at equal distances. 1.732m, 1.1077m, 1.654 m
40) A boyis standing on the ground and flying a kite with 100m of string at an elevation of 30°. Another boy is standing on the roof of a 10m high building and is flying his kite at an elevation of 45°. Both the boys are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the two kites meet. 40√2m
41) The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of elevation of the top of the tower from the foot of the hill is 30°. If the tower is 50m high , what is the height of the hill ? 150m
42) Two boats approach a light house in mid-sea from opposite directions. The angles of elevation of the top of the lighthouse from two boats are 30° and 45° respectively. If the distance between two boats is 100m, find the height of the light house . 50(√3-1)
43) From the top of a building AB, 60m high , the angle of the depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find
a) the horizontal distance between AB and CD. 34.64m
b) the difference between the heights of the building and the lampost. 20m
44) From the top of a lighthouse, the angles of depression of two ships on the opposite sides of it are observed to be α and β. If the height of the lighthouse be h metres and the line joining the ships passes through the foot of the light house , show that the distance between the ship is h(tanα + tanβ)/(tanα tanβ). metres
45) A straight highway leads to the foot of a tower of height 50m. From the top of the tower, the angle of depression of two cars standing on the highway are 30° and 60° respectively. What is the distance between the two cars and how far is each car from the tower ? 57.67m, 86.5m, 28.83m
46) The angles of elevation of the top of a rock from the top and foot of a 100m high tower are respectively 30° and 45°. Find the height of the rock. 236.5m
47) As observed from the top of a 150m tall light house, the angles of depression of two ships approaching it are 30° and 45°. If one ship is directly behind the other, find the distance between two ships. 109.5m
48) A flagstaff stands on the top of a 5m high tower. From a point on the ground, the angle of elevation of the top of the flagstaff is 60° and from the same point, the angle of elevation of the top of the tower is 45°. Find the height of the flagstaff. 3.65m
50) The angle of elevation of the top of the tower from a point A in the ground is 30°. On moving a distance of 20 m towards the foot of the tower to a point B the angle of the elevation increases to 60°. Find the height of the tower and the distance of the tower from the point A. 17.3m, 30m
51) From the top of a building 15m high the angle of elevation of the top of a tower is found to be 30°. From the bottom of the same building, the angle of elevation of the top of the tower is found to be 60°. Find the height of the tower and the distance between the tower and building. 22.5m, 12.975m
6) The length of a string between a kite and a point on the ground is 90m. If the string makes an angle θ with the ground level that tanθ = 15/8, how high is the kite? Assume that there is no slack in the string. 79.41 m
32) The angle of elevation of a stationery cloud from a point 2500m. Above a lake is 15° and the angle of the depression of its reflection is 45°. What is the height of the cloud above the lake level ? 2500√3
49) The angle of elevation of the top of a tower as obsorved from a point in a horizontal plane through the foot of the tower is 32°. When the observer movrs towards the tower distance and the first position from the tower. 93.64m, 46.7m






No comments:
Post a Comment