SHARES AND DIVIDEND
1) The total amount of money needed to run the company is called:
a) shares b) capital c) dividend d) principle
2) The whole capital to run a company is divided into small units, called:
a) Shares b) Share holders c) face value d) dividend
3) The annual profit distributed among share holders is called:
a) nominal value b) market value c) dividend d) face value
4) The value of a share printed on the share certificate is called its :
a) nominal value b) market value c) discount d) below par
5) The shares of different companies can the brought or sold in the market through stock exchange. The price at which the share is share or purchased is called its
a) face value b) market value c) par value d) Nominal value
6) A share is said to be____, if its market value is the same as its face value.
a) premium b) discount c) par c) nominal value
7) A share is said to be at premium, if its market value is ____then its face value.
a) more b) less c) same d) equal
8) A share is said to be____, if its market value is less than its face value.
a) At par b) above par c) below par d) premium
9) The face value of a share
a) change every year b) changes from time to time c) always remains the same d) none to
10) Dividend is always paid on the____ of a share.
a) market value b) face value c) investment d) dividend
11) The market value of a share.
a) never changes b) changes from time to time c) changes every month d) none
12) Number of share hold by a person=
a) total nominal value/face value of one share
b) total market value/ face value of one share.
c) dividend/market value of one share.
d) dividend/investment x 100
13) dividend =
a) number of shares x nominal value
b) number of shares x market value
c) face value x number of shares x rate of dividend/100
d) none
14) Rate of return on investment=
a) investment/dividend
b) dividend/investment
c) dividend/ investment x 100
d) investment/dividend x 100
15) investment/ sale proceeds =
a) number of shares x market value
b) number of shares x nominal value
c) face value x number of shares x rate of dividend
d) dividend/investment
16) annual income of a share holder
a) number of shares x face value
b) number of shares x rate of dividend x face value of 1 share
c) number of shares x market value x face value
d) market value x nominal value x 100
17) If a share of of Rs100 is selling at Rs125, then it is said to be selling at a ___ of Rs25.
a) discount b) premium c) at par d) below par
18) if a share of Rs125 is selling at Rs96, then it is said to be selling at Rs 29___.
a) below par b) at par c) above par d) premium
19) if Kabir invests Rs 10320 on Rs100 shares at a discount of Rs14, then the number of shares he buys is
a) 110 b) 121 c) 150 d) 100
20) Shahrukh has some shares of Rs50 of a company paying 15% dividend. If his annual income is Rs 3000, then the number of shares he processes is
a) 400 b) 600 c) 800 d) 200
21) If Kiran invests Rs19250 on Rs50 shares at a premium of 20%, then the number of shares she buys is
a) 640 b) 160 c) 320 d) 240
22) Varun possesses 600 shares of Rs25 of a company. If the company announces a dividend of 8%, then his annual income is
a) Rs600 b) Rs1200 c) Rs480 d) Rs120
23) A man invests Rs24000 on Rs60 shares at a discount of 20%. If the dividend declared by the company is 10%, then his annual income is
a) Rs2880 b) Rs1500 c) Rs3000 d) none
24) Rs25 shares of a company are selling at Rs20. If the company is playing a dividend of 12%, then the rate of return is
a) 10% b) 18% c) 15% d) 12%
25) Rs 40 shares of a company are selling at 25% premium. If Mr Washim wants to buy 280 shares of the company, then the investment required by him is
a) Rs14000 b) Rs16800 c) Rs8400 d) Rs10000
SHORT ANSWERS:
1) Find the % return on investment in
a) 6% Rs100 shares at Rs120
b) 25/3% Rs100 share at Rs150
2) Find the price of 5% Rs100 shares when an investor gets a dividend of Rs65 by investing Rs1430.
3) At what price should a 25/4% Rs 100 shares be quoted when the money is worth 5%
4) A person invested Rs1284 in 8/2% Rs100 shares . His dividend was Rs54. Calculate the M.V of the shares.
5) A company pays 7% dividend . For how much should a man buy a Rs100 shares for getting 8% on his investment.
6) Which share is more profitable: 4% Rs100 share at Rs80 or 9/2% Rs100 share at Rs88 ?
7) A part of Rs3020 is invested in 6% Rs100 shares at Rs97 and the rest in 12% Rs100 share at Rs108. If both bring the same dividend, find the sum invested in the share selling
a) at discount
b) above par
c) the total dividend
8) A person bought 360 ten rupee share paying 12% dividend at par and sold them at Rs21. The proceeds were invested in 5 rupees shares paying 9/2% at 3.5 per share. Find
a) sale proceeds
b) the number of 5 rupees shares bought
c) the percentage in income
9) A person invests Rs4368 in 100 rupees share at Rs91. Shares worth Rs24000 face value are sold at Rs95 and the rest at Rs85. Find
a) the number of shares bought Rs91
b) the number of shares sold at Rs85
c) the loss or gain in the deal .
10) Rs8000 and Rs 10000 were invested in Rs100 shares giving dividends 12% and 8% respectively. The dividend are collected and all the shares are sold at a loss of 2% and 3% respectively on the investment. Find
a) the dividend collected
b) the total sell proceeds
c) gain percent on the whole transaction.
LONG ANSWER
1) A man has a choice to invest in Rs 100 shares of two firms at Rs120 each or at Rs132 each. The first firm pays a dividend at 5% per annum and the second firms pays a dividend of 6% per annum. How much more will his annual return be if he invests Rs 26400 with the firm from which he gets a better return on his investment ?
2) A man bought one thousand shares each of face value Rs5 at Rs7 per share . At the end of the year, the company from which he bought the shares declared a dividend of 8%. Calculate
a) the amount of money invested by the man
b) the percentage return on his outlay. (Correct to one decimal place).
3) Ajay owns 560 share of a company. The face value of each share is Rs25. The company declares a dividend of 9%. Calculate
a) the dividend that Ajay will get.
b) the rate of interest on his is investment, if Ajay had to pay Rs30 for each share.
4) A company with 4000 shares of nominal value of Rs110 each declares an annual dividend of 15%. Calculate
a) the total amount of dividend paid by the company.
b) the annual income of shah Rukh who holds 88 shares of the company.
c) If he received only 10% on his investment, find the price Shah Rukh paid for each share.
5) Amit Kumar invests Rs36000 in buying Rs100 shares at Rs20 premium. The dividend is 15 percent per annum. Find
a) the number of shares he buys .
b) his yearly dividend
c) the percentage return on his investment
6) Vivek invested Rs45000 in 8% Rs10 shares at Rs15 sells the shares when the price rise to Rs30 and invests the proceeds in 12% Rs100 shares at Rs125. Calculate
a) the sale proceeds
b) the number of Rs125 shares he buys
c) the change in his annual income from dividend.
MATRIX
1) Which of the following is a row matrix ?
a) matrix P of order 2x2
b) matrix Q of order 1x2
c) Matrix R of order 2x1
d) Matrix S of order 3x2
2) The order of matrix is 2x3. It has:
a) 5 element b) 6 elements c) 1 elements d) none
3) If A= 4 -2 B= 3 5 & C= 1 3
5 7 -4 -2 -2 4 , then the value of A+ B C is
a) 6 1 b) 6 0 c) 6 3 d) 6 6
3 0 3 1 0 1 3 1
4) If A= 4 x & B= y -3 C= 10 0 with the relation 3A+ 2B = C, then:
a) x=1, y=0 b) x=-1, y=0 c) x=2, y= -1 d) x=-2, y=1
5) Order of matrix A is 2x3 and the order of matrix B is 3x1. The order the matrix AB is:
a) 2x1 b) 1x 2 c) 3 x 1 d) 2x 3
6) Which of the following is a diagonal Matrix ?
a) 0 6 1 b) 2 0 0
2 0 4 0 -1 0
1 8 0 0 0 -2
c) 4 0 0 d) 1. 0 0
0 -2 0 0 1 1
0 0 1
7) In a null matrix:
a) all the elements are 0
b) every diagonal element is zero
c) every non-diagonal element is zero
d) every element is one.
8) 1 8 9 is a:
a) row matrix b) column matrix c) diagonal matrix d) null matrix
9) The transpose of matrix
2 -1 4
1 7 3
-4 1 5 is:
a) 2 1 4 b) 2 4 -1
-1 1 5 1 3 7
4 7 3 -4 5 1
c) -1 4 2 d) 2 1 -4
7 3 1 -1 7 1
1 5 -4 4 3 5
10) The order of matrix A is 2x 3 and that of B is 3x1.
a) AB is possible, but BA is not possible.
b) BA is possible but AB is not possible
c) AB as well as BA are not possible
d) AB as well as BA are possible
11) if A= 2 -4 & B= 1 -1
0 1 0 5, then the value of B+ A is
a) 3 -5 b) 6 2 c) 1 -2 d) -3 5
0 6 -1 4 -4 1 0 -6
12) If A= 2 5 B= 1 -1
1 3 -3 2 then AB is equal to
a) -13 5 b) 8 -1 c) -13 8 d) -1 0
1 8 5 2 -8 5 7 -2
13) If A= 3 -4 &B= -1 2
5 6 5 7 then the order of 3A - 2B is
a) 2x1 b) 4x4 c) 1x1 d) 2x2
14) If A= 2 5 & B= 1 -3
-3 7 2 5 then B - A is equal to
a) 4 -1 b) -1 -8 c) -1 8 d) -2 4
6 -2 5 -2 5 4 -1 -2
15) If M= 1 -2 & N= 2 1
-1 2 then the order of MN is
a) 1x2 b) 2x1 c) 1x1 d) 2x2
16) If A= -2 3 B= 5 2
4 5 -7 3 then transpose of matrix (A+ B) is:
a) 3 5 b) 3 -3 c) 3 8 d) 3 5
-3 8 5 8 -3 5 -8 3
17) If A= 2 1 & B= 5 -1
-1 4 2 -1 then Aᵗ - Bᵗ is equal to:
a) 1 -1 b) 7 -1 c) -3. -1 d) -3 -3
4 2 2 5 2 4 2 5
18) If A= 1 2 B= x. 0
3 3 0 y then the order of the matrix BA is
a) 1x2 b) 2x1 c) 2x3 d) 2x2
19) If A= 2 0 B= 0 1
-3 1 -2 3 then the matrix BA is
a) -3 1 b) -4 5 c) -3 2 d) 4 -1
-13 3 -2 7 5 -7 2 19
20) If A= x 3 & A²= 3I, where I= 1 0
y 3. 0 1 the order of A² is
a) 2x2 b) 2x3 c) 1x2 d) 3x2
Short Answer type Questions
1) If A= 3 -1
0 2 find matrix B such that A²- 2B = 3A + 5I, where I is 2x2 identity matrix.
2) Given matrix
A= 4sin30° cos0° & B= 4
Cos0° 4sin30° 5 if AX = B
a) Write the order of matrix X.
b) Find the matrix X.
3) Find the value of x and y if
A= x 7 B= 6 -7 C= 10 7
9 y-5 4 5 22 15 with the relation 2A+ B = C
4) Simplify:
A= sinA -cosA & B= cosA sinA
CosA sinA -sinA cosA with the relation A sinA+ B cosA
5) A= x 3
y 3 if A²= 3I where I is the identity matrix of order 2, find x and y
6) A= 1 4 & B= 3 2
-2. 3. 0 -3 with the relation A+ 2M = 3B, find the matrix M
7) If A= p 0 B= 0 -q C= 2 -2
0 2 1 0 2 2 and BC = C², find the values of p and q
8) If A= 2x x B= 3 & C= 16
y 3y 2 9 with the relation AB = C then find x and y
9) If A= 3 -2 B= 6 C= -4 D= 2
-1 4 1 5 2 find the value of AB+ 2C - 4D.
10) Evaluate:
A= 4sin30 2cos60 B= 4 5
Sin90 2 cos0 5 4 find the value of AB
LONG ANSWER TYPE QUESTIONS
1) If A= 2 5 B= 4 -2
1 3 -1 3 and I is the identity matrix of the same order and A' is the transpose of matrix A, find A'B + BI.
2) Let A= 2 1 B=4 1 & C=-3 2
0 -2. -3 -2 -1 4 find A²+ AC - 5B
3) A= 2 0 I= 1 0
-1 7 0 1 and A²= 9A + mI. Find m.
4) If A= 1 3 B= -2 1
3 4 -3 2 and A²- 5B²= 5C, find matrix C, where C is a 2 by 2 matrix.
5) B= 1 1
8 3 find the matrix X if X= B²- 4B. Hence solve for a and b given
X= a & C= 5
b 50 with X= C
6) If A= 2 3 B= 0 4 C= 1 0
5 7 -1 7 -1 4, find AC + B²- 10C.
7) If A= 4 2
-1 1 with relation AM=6I where M is a matrix and I is unit matrix of order 2x2.
a) State the order of oM
b) Find the matrix M.
8) A= 3 0 B= -4 2
5 1 1 0 find A²- 2AB + B².
PROBABILITY
Multiple Choice Questions
1) If an event cannot occur, then its Probability is:
a) 1 b) 3/4 c) 1/2 d) 0
2) Which of the following cannot be the probability of an event?
a) 1/3 b) 0.1 c) 3% d) 17/16
3) An event is very unlikely to happen. Its Probability is closest to:
a) 0.0001 b) 0.001 c) 0.01 d) 0.1
4) If the probability of an event is p, The probability of its complementary event will be:
a) p -1 b) p c) 1- p d) 1- 1/p
5) Which of the following can be the probability of an event?
a) -0.04 b) 1.04 c) 18/23 d) 8/7
6) If P(A) denotes the probability of an event A, then
a) P(A) <0 b) P(A)>1 c) 0≤ P(A)≤ 1 d) -1≤ P(A)≤ 1
7) A card is selected from a deck of 52 cards. The probability of its being a red face card is :
a) 3/26 b) 3/13 c) 2/13 d) 1/2
8) The Probability that a non leap year selected at random will contains 53 Sundays is:
a) 1/7 b) 2/7 c) 3/7 d) 5/7
9) When a die is thrown, the probability of getting an odd number less than 3 is:
a) 1/6 b) 1/3 c) 1/2 d) 0
10) If a letter is drawn at random from the letters inword ERROR, then the letters which have equal probability of being drawn are:
a) E and O b) R and E c) O and R d) E, R and O
11) From the data (1, 4, 9, 16, 25, 29) if 29 is removed , then the probability of a getting a number which is neither a prime nor a composite is:
a) 2/5 b) 1/5 c) 3/5 d) 4/5
12) A game of chance consisting of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 and these are equally likely outcomes. Then, the probability that it will point at a prime number is
a) 1/8 b) 5/8 c) 3/8 d) 1/2
13) It is given that in a group of three students, the probability of two students not having the same birthday is 0.991. then, the probability of the two students having the same birthday is :
a) 0.009 b) 0.001 c) 0.990 d) 0.007
14) If the probability of success is 38%, then the probability of failure is:
a) 38% b) 62% c) 52% d) 68%
15) In a flower bed, every third plant is a rose plant. if a child picks a flower, then the probability of the flower being other than rose is :
a) 1/5 b) 1/3 c) 2/3 d) 2/5
16) Two dice are thrown together. The probability of getting the same number on both the dice is
a) 1/2 b) 1/3 c) 1/6 d) 1/12
17) A card is drawn from a pack of 52 cards. The event E is that the card is not an ace of hearts. The number of outcomes favourable to E is:
a) 4 b) 14 c) 21 d) 51
18) The probability of a getting a bad egg in a lot of 400 is 0.035. The number of bad eggs in the lot is :
a) 7 b) 14 c) 21 d) 28
19) A girl calculates that the probability of her winning the first prize in a lottery is 0.08. if 6000 tickets are sold, how many tickets has she bought ?
a) 40 b) 240 c) 480 d) 750
20) One ticket is drawn at random from a bag containing tickets numbered 1 to 40. The probability that the selected ticket has a number which is a multiple of 5 is :
a) 1/5 b) 3/5 c) 4/5 d) 1/3
21) Someone is asked to take a number from 1 to 100. The probability that it is prime is:
a) 1/5 b) 6/25 c) 1/4 d) 13/50
22) In a single throw of 2 dies, the probability of getting 6 as a product is:
a) 4/9 b) 2/9 c) 1/9 d) 5/9
23) The probability of getting an even number, when a die is thrown once, is
a) 1/2 b) 1/3 c) 1/6 d) 5/6
24) Many birds were sitting on a tree. Every seventh bird was a sparrow. A bird flew away. What is the probability that the bird was not a sparrow?
a) 5/7 b) 3/7 c) 6/7 d) 1/7
25) A box contains cards numbered 6 to 50. A card is drawn at random from the box. The probability that the drawn card has a number which is a perfect square is
a) 1/45 b) 2/15 c) 1/9 d) 4/45
Short Answer Type Questions
1) A Jar contains 24 marbles, some are green and other are blue. If a marble is drawn at a random from the jar, the probability that it is given is 2/3. Find the number of blue marbles in the jar.
2) A bag contains 100 identical marble stones numbered from 1 to 100. What is the probability of drawing a marble having a number divisible by both 4 and 5.
3) A card is drawn at random from a well shuffled pack of 52 cards. Find the probability that the card is black or king.
4) From a set of 17 cards numbered 1,2,3,....17, one card is drawn at random. What is the probability that number on the drawn card is multiple of 3 or 7?
5) There are 5 green, 6 black and 7 white balls in a bag. A ball is drawn at random from the bag. Find the probability that it is not a white.
6) If an unbiased dice is thrown 5 times and every throw resulted in a 6, what is the probability of getting a 6 on the sixth throw.
7) A card is drawn at random from a well shuffled deck of 52 cards. What is the probability that the card drawn is a diamond?
8) A ball is chosen from a bag that contains 30 balls numbered from 1 to 30. What is the probability that the ball chosen will have a number that is divisible by 3?
Long Answer Type Questions
1) 5 defective glasses are accidentally mixed with 20 good ones. The good glasses and the defective one look same. If a glass is chosen at random, what is the probability that the chosen glass is good?
2) A box of 15 chocolates has 6 that contains caramel. 5 that contain nuts and 4 that contain cashews. If you randomly selected a chocolate, what is the probability that you will get one that contains nuts?
3) A bag contains red, blue and green balls. It is twice as likely to pick a blue ball as a compared to a red ball, it is thrice as likely to pick a green ball as compared to a red ball. What is the probability of picking a green ball?
4) A dice is thrown twice. Find the probability of getting a bigger value on the first throw.
5) A box contains 3 black balls, 4 red balls and 3 green balls. All the balls are identical in shape and size. Rohit takes out a ball from the bag without looking into it. What is the probability that the ball drawn is a black or green ball.
6) Two dice are thrown at the same time. Write down all the outcomes. Find the probability that the sum of the two number appearing on the dice is.
a) 8 b) 13 c) lesser than or equal to 12.
7) A card is drawn at random from a pack of cards. Find the probability of getting
a) a red king.
b) a queen or a Jack.
ANGLE AND CYCLIC
PROPERTIES OF A CIRCLE
Multiple Choice Questions
a) 20 b) 40 c) 60 d) 10
2) In the figure,angle PQR=100°, where P, Q and R are points on a circle with centre O, then angle OPR=
a) 15 b) 12 c) 10 d) 8
a) 60 b) 70 c) 80 d) 100
a) 30 b) 60 c) 90 d) 45
a) 50 b) 40 c) 60 d) 70
6) In the figureA, B and C are 4 points on a circle. AC and BD interesect at a point E such that angle BEC = 130° and angle ECD= 20, then angle BAC=
a) 100 b) 102 c) 50 d) 110
7) ABCD is a cyclic quadrilateral whose diagonals Intersect at a point E. If Angle DBC=70°, and angle BAC=30°, then angle BCD=
a) 60 b) 70 c) 80 d) 75
a) 50 b) 45 c) 40 d) 35
a) 18 b) 28 c) 32 d) 46
10) ABCD is a parallelogram.A circle passes through A and D, cuts AB at P and DC at Q. If ang BPQ=80°, then angle ABC is
a) 60 b) 75 c) 80 d) 105
11) In the given figure,AB and CD are two equal chords of a circle with centre O. OP and OQ are perpendicular on chord AB and CD respectively. If Angle POQ= 140°, then angle APQ is
a) 70 b) 80 c) 95 d) 105
12) In the given figure,O is the centre of the circle. If Angle OPR and OQR are 40° and 30° respectively then, the measure of angle POQ is
a) 160 b) 150 c) 140 d) 130
a) 40 b) 50 c) 60 d) 75
a) 115 b) 120 c) 135 d) 150
15) In the given figure,O is the centre of the circle. If Ang PAQ=120° and angle RQS=25°, then the measure of angle PRQ is
a) 95 b) 105 c) 115 d) 135
a) 60 b) 50 c) 70 d) 80
17) ABCD is a cyclic quadrilateralsuch that AB is a diameter of the circle circumscribing it and angle ADC=130°, then angle BAC is
a) 80 b) 50 c) 40 d) 30
a) 30 b) 45 c) 90 d) 60
19) In the figure,O is the centre of the circle. The angle subtended by the arc BCD at the centre is 140°, BC is produced to P, then angle BAD+ angle BCD=
a) 160 b) 170 c) 180 d) 210
20) In the figure,chord ED is parallel to the diameter AC of the circle. Given angle CBE=65°, then angle DEC=
a) 35 b) 30 c) 25 d) 20
a) angle A B) Ang B c) angle C d) none
a) 86 b) 84 c) 82 d) 80
Short Questions
1) In the given figure,angles subtended by arc AC and BC at the centre O of the circle are 55° and 155° respectively. Find angle ACB.
2) BC is a chord of a circle with centre O.A is a point on major arc BC as shown in the figure. Show that angle BAC+ angle OBC= 90°.
3) Two circles Intersect at two points A and B.AD and AC are diameters of the two circles. Prove that B lies on the line segment DC.
4) ABCD is a cyclic quadrilateral whose diagonals Intersect at a point E,if Ang DBC=70°, angle BAC= 30°, find angle BCD. Further, if AB= BC, find angle ECD.
5) In the given figure,AB is a diameter of the circle. Angle BDC=20° and angle CBD=25°. Find angles AED and ACD.
6) In the given figure,ABCD is a cyclic quadrilateral O is the centre of the circle. If Angle COD=120° and angle BAC= 30°, find angles BOC and BCD.
a) angle BCD.
b) angle ADB. Hence, show that AC is a diameter of the circle.
8) In the figure A, D, B, C are four points on the circumference of a circle with centre O. arc AB= 2 arc BC and angle AOB= 108°. Calculate in degree
a) Ang ACB
b) angles CAB
c) Ang ADB .
9) In the given figure,AB is a diameter of the circle. PQ is a chord such that angle BAPA= Ang ABQ. Show that ABQP is a cyclic trapezium.
Long Answer Type Questions
2) In the given figure,AC is the diameter of the circle with Centre O. CD and BE are parallel, angle AOB=80° and angle ACE= 10°, calculate the angles BEC, BCD, CED.
3) In the figure,O is the centre of the circle. Angle AOE= 150°, angle DAO= 51°. Calculate the measure of angles BEC, EBC.
4) Two circles Intersect at P and Q. Through P,a straight line APB is drawn to meet the circles in A and B. Through Q, a straight line is drawn to meet the circles at C and D. Show that AC is parallel to BD.
TANGENT PROPERTIES OF CIRCLES
Multiple Choice Questions
1) In the given figure,TAS is a tangent to the circle, with centre O, at point A. If Angle OBA=32°, then the value of x will be:
a) 19 b) 38 c) 58 c) 76
2) A point P is 10cm from the centre O of a circle. The length of the tangent drawn from P to the circle is 8cm. The radius of the circle is equal to:
a) 4cm b) 5cm c) 6cm d) 8cm
3) In the given figure,PT is a tangent to the circle with centre O. If OT= 6cm and OP= 10cm, then the length of tangent PT is
a) 8cm b) 12cm c) 10cm d) 16cm
4) In the given figure,AC is a chord of the circle and AOC is its diameter such that angle ACB=50°. If AT is the tangent to the circle at a point A, then angle BAT is equal to
a) 65 b) 60 c) 50 d) 40
5) In the figure,AT is a tangent to the circle with centre O such that OT= 4cm and angle OTA=30°. The length of AT is
a) 4cm b) 2cm c) 2√3cm d) 4√3 cm
6) In the figure,chords AB and CD intersect at P. If PA= 6cm, PB= 5cm and CD= 13cm, then the length of PC is
a) 10cm b) 8cm c) 6cm d) 5cm
7) In the figure,PA and PB are tangents to the circle with centre O such that angle APB=50°, then the measure of angle OAB is
a) 37 b) 36 c) 50 d) 25
8) Tangents PQ and PR are drawn from an external point P to a circle with centre O,such that angle RPQ=30°. A chord RS is drawn parallel to the tangent PQR. Then angle RQS is
a) 40 b) 30 c) 25 d) 20
9) In the figure,PQ is a chord of a circle with centre O and PT is a tangent. If QPT = 60°, then angle PRQ is
a) 130 b) 120 c) 110 d) 100
10) In the figure,O is the centre of the circle. PT and PQ are tangents to the circle from an external point P. If Angle TPQ=70°, then angle TRQ is
a) 60 b) 58.5 c) 55 d) 50
11) In the figure,PA and PB are tangents to a circle with centre O, such that AP= 5cm and angle APB=60°, then the length of chord AB is
a) 9cm b) 5cm c) 4.5cm d) 4cm
12) In the figure,PQ is a tangent at a point C to a circle with centre O. If AB is a diameter and angle CAB=30°, then angle PCA is
a) 60 b) 58 c) 57 d) 56
13) In the figure,O is the centre of the circle, AB is a chord and AT is the tangent at a point A. If Angle AOB= 100°, then angle BAT is
a) 30 b) 40 c) 50 d) 100
14) Point P is 25cm away from the centre O of a circle and the length PT of the tangent drawn from P to the circle is 24cm. The radius of the circle is
a) 7cm b) 9cm c) 10cm d) 12 cm
15) In the figure,TP and TQ are two tangents to a circle with centre O such that, angle POQ=110°, the value of angle PTQ is
a) 60 b) 65 c) 70 d) 75
16) In the figure,AB is the diameter of a circle with centre O and AT is a tangent. If Angle AOQ= 60° , then angle ATQ is
a) 60 b) 50.5 c) 49 d) 30
17) In the figure,AOB is a diameter of a circle with centre O and AC is a tangent to the circle at Q. If Angle BOC=130°, then angle ACO is
a) 35 b) 38 c) 120 d) 40
18) In the figure,CP and CQ are tangents to a circle with centre O. ARB is another tangent touching the circle at R. If CP= 11cm and BC= 7 cm, then the length of BR is
a) 3.5cm b) 4cm c) 3cm d) 11cm
19) In the figure,PA and PB are two tangents from an external point P to a circle with centre O. If Angle PBA= 65°, then angle OAB is
a) 15 b) 25 c) 35 d) 45
20) In the figure,PA and PB are tangents to the circle with centre O. If Angle APB= 60°, then angle OAB is
a) 40 b) 30 c) 25 d) 20
Short Answer Type Questions
1) In the figure PA and PB are tangents to the circle drawn from an external point P. CD is another tangent touching the circle at Q. If PA= PB= 12cm and QD= 3cm, find the length of PD.
2) In the figure,PA and PB is a pair of tangents drawn to a circle having its centre at O. If Angle APB= 52°, find angles PAB, PBA.
3) A point P is 15cm from the centre of a circle. The radius of the circle is 5cm. Find the length of the tangent drawn to the circle from the point P.
4) In the figure,the circle touches the sides BC, CA and AB of ∆ ABC at D, E and F respectively. If AB= AC, show that BD= CD.
5) A circle is touching the side BC of a ∆ ABC at P and touching AB and AC produced at Q and R respectively. Show that AQ= (1/2) perimeter of ∆ ABC.
6) Show that the tangents drawn at ends of a diameter of a circle are parallel.
7) A quadrilateral ABCD is drawn to circumscribe a circle, as shown in the figure.Show that AB+ CD= AD+ BC.
8) In the figure,a circle touches all the four sides of a quadrilateral ABCD with AB= 6cm, BC=7cm and CD= 4cm. What is the length of AD?
9) In the figure,O is the centre of the circle, PQ is a tangent to the circle at A. If angle PAB =58°, find angles ABQ and AQB.
Long Answer Type Questions
1) PQ is a chord of length 8cm of a circle of radius 5cm.The tangents at P and Q intersect at a point T. Find the length of TP.
2) In the figure,AB is diameter of a circle with centre O and QC is a tangent to the circle at C. If Angle CAB=30°, find angles CQA, CBA.
3) ABC is a right angle triangle, right angled at B. A circle is inscribed in it. The length of the two sides containing the right angle are 6cm and 8cm. Find the radius of the circle.
4) Two tangents PA and PB are drawn to the circle with centre O, such that angle APB= 120°. Show that OP= 2AP.
5) Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Show that angle PTQ= 2 angle OPQ.
6) A circle is inscribed in a ∆ ABC having sides 8cm, 10cm and 12cm as shown in the figure.Find AD, BE, and CF.
CHOOSE THE CORRECT OPTION:
20) The product of two roots of the equation x²-7x +3 =0 is
a) 7 b) -7 c) 3 d) - 3
23) Under what condition one root of the quadric equation ax²+ bx + c=0 is zero ?
a) a= 0 b) b= 0 c) c= 0 d) none.
24) 2x²- 3x - k +2=0 one root of the equation is 0. The value of k is
a) 2 b) -2 c) 1/2 d) -1/2
25) If a/b = b/4 = c/7 then, the value of (a+ b+ c)/c
a) 1 b) 2 c) 3 d) 4
26) The mean proportional of 9 and 25 is
a) 20 b) 21 c) 41 d) 441
28) If two roots of equation x²+ 4x +k=0 are equal, then the value of k is
a) 1 b) 2 c) 3 d) 4
29) If two roots of equation x²- 6x + k=0 are real and unequal then what is the value of k ?
a) more than 6 b) less than 6 c) more than 9 d) less than 9.
30) The sum of two roots of the equation x²- 6x +2=0
a) 2 b) - 2 c) 6 d) - 6
31) If the product of two roots of the equation is x²- 3x + k=10 is -2, what is the value of k ?
a) - 2 b) - 8 c) 8 d) 12
32) If two roots of the equation ax²+ bx + c=0(a≠ 0) be equal , then
a) c= -b/2a b) c= b/2a c) c= - b²/4a d) c= b²/4a
33) The roots of the equation x²= 6² is/are
a) 0 b) 6 c) 0 and 6 d) - 6
34) if two roots of the equation (k +1)x²+ 2kx + (k +2)= 0 are equal and negative then the value of k is
a) 1 b) -1 c) 0 d) -2
35) If the roots of the equation ax²+ bx + c=0(c ≠ 0) are real and unequal then b²- 4ax will be
a) >0 b) =0 c) <0 d) none.
36) The number of roots in a quadratic equation is
a) 1 b) 2 c) 3 d) none.
37) If ax²+ bx + c=0 is a quadratic equation then
a) b≠ 0 b) c≠ 0 c) a≠ 0 d) none.
38) The highest power of the variable of a quadratic equation is
a) 1 b) 2 c) 3 d) none
39) The equation 4(5x²- 7x +2)= 5(4x²- 6x +3) is
a) linear b) quadratic c) 3rd degree d) none
40) third proportion of 8 and 12 is
a) 12 b) 16 c) 18 d) 20
41) a is a positive number and if a: 27/64 = 3/4: a, then the value of a is :
a) 81/256 b) 9 c) 9/16 d) 16/9
42) 2a = 3b = 4c then value of a :b :c is
a) 3:4:6 b) 4: 3: 6 c) 3:6:4 d) 6:4:3
51) The length of the two chords AB and CD cycle of a circle of centre O are equal and angle AOB= 60°,then angle COD= is
a) 40° b) 30° c) 60° d) 90°
52) O is the centre of a circle and AB is a diameter, ABCD is a the cyclic quadrilateral.Angle ABC=65°, angle DAC= 40°, then the measure of angle BCD is
a) 75° b) 105° c) 115° d) 80°
53) If Angle A =100° of a cyclic quadrilateral ABCD, then the value of angle C is
a) 50° b) 80° c) 180° d) 200°
54) The number of common tangents of two circles when they do not touch or intersect each other is :
a) 2 b) 1 c) 3 d) 2
55) The length of the radius of 6 circle is 13cm and the length of a chord of the circle is 10cm, the distance of the coord from the centre of the circle is
a) 12.5cm b) 12 cm c) √69cm d) 24 cm
56) The centre of two concentric circles is O; a straight line intersects a circle at point A and B and the other circle at point C and D. If AC= 5 cm, then the length of BD is
a) 2.5cm b) 5cm c) 10 cm d) none.
57) The distance between two parallel chords of length 8cm each in a circle of diameter 10 cm is
a) 6cm b) 7cm c) 8cm d) 5.5 cm
a) 70° b) 60° c) 40° d) 200°
59) In the adjoining figure,if O is the centre of the circle and the BC is the diameter then the value of x is
a) 60° b) 50° c) 100° d) 80°
60) In the adjoining figure,O is the centre of the circle; if ang ACB =30°, angle ABC= 60°, angle DAB= 35° and DBX= x°, then the value of x is
a) 35 b) 70 c) 65 d) 55
61) If AB is a diameter of a circle with Centre O and C is a point on the circumference such that angle BOC=60°, then the value of angle AOC is
a) 60° b) 30° c) 120° d) 90°
62) In the adjoining figure,O is the centre of the circle and AB is the diameter. If AB || CD, angle ABC=25°, then the value of angle CED is
a) 80° b) 50° c) 25° d) 40°
65) In the adjoining figure,O is the centre of the circle, id angle BCD= 28°, angle AEC= 38°, then the value of angle AXB= ?
a) 56° b) 86° c) 38° d) 28°
66) In the diagrambesides O is the centre of the circle and AB is a diameter. ABCD is a cyclic quadrilateral. Angle BAC is
a) 50° b) 60° c) 30° d) 40°
67) In the diagrambesides ABCD is a cyclic quadrilateral. BA is produced to the point F. If AE|| CD, angle ABC= 92° and angle FAE= 20°, then the value of angle BCD is
a) 20° b) 88° c) 108° d) 72°
68) I is the centre of ∆ ABC, angle ABC= 60° and angle ACB= 50°. Then angle BIC is
a) 55° b) 125° c) 70° d) 65°
69) In the adjoining figure,O is the centre of the cirle, if Angle BAD= 65°, angle BCD= 45°, then the value of angle BCD is
a) 65° b) 45° c) 40° d) 20°
71) If tanx + cotx =2, then the value of (tan¹³x + cot¹³x) is
a) 1 b) 0 c) 2 d) none
80) Height of tower is 100√3 metres. The angle of elevation of the top of the tower from a point at a distance 100metres from the foot of the tower is
a) 30° b) 45° c) 60° d) none
83) If the ratio of the volume of two right circular cones is 1:4 and the ratio of radii of their bases is 4:5, then the ratio of their height is:
a) 1:5 b) 5:4 c) 25: 16 d) 25 :64
84) If two cubes of length of each side 2√6 are placed side by side, then the length of the diagonal of the cuboid so produce is
a) 10cm b) 6cm c) 2cm d) 12cm
85) If side of a cube is a unit and the diagonal of the cube is d unit then the relation between a and d will be:
a) √2 a= d b) √3 a = d c) a= √3 d d) a= √2 d
86) If each of radius of the base and height of a cone be doubled, then the volume of it will be
a) 3 times b) 4 times c) 6 times d) 8 times
87) If the height of a cone is h unit, slant height I units and the diameter of the base is d unit, then (l²- h²)/d²= ?
a) 1/2 b) 1/3 c) 1/4 d) 1/5
88) The volume inside a rectangular box is 440 cubic cm and the area of the inner base is 88 sq cm, then the inner height of the box is
a) 4cm b) 5cm c) 3cm d) 6 cm
89) A rectangular pit is 40m long , 12m wide and 16m deep. In this pit a plank 5m long, 4 m wide and 2 m high will be placed ?
a) 190 b) 192 c) 184 d) 180
90) The area of the lateral plane of a cube is 256 sq.m volume of cube
a) 64cune m b) 216 cube m c) 256 cube m d) 51 cube m
91) If the ratio of the volumes of two cubes is 1:27, then the ratio of the area of the total surface of both the cubes is
a) 1:3 b) 1 : 8 c) 1: 9 d) 1:18
92) if the area of all the sides of a cube is 5 square unit and the length of the diagonal is d units, then the contact between S and d is
a) S= 6d² b) 3S= 7d c) S³= d² d) d²= S/2
93) If the ratio of the radii of two circular solid cylinder 2 :3 and the ratio of their height is 5:3, then the ratio of the areas of their sides is
a) 2:5 b) 8 : 7 c) 10:9 d) 16:9
94) if the ratio of the radiu of two right circular solid cylinder is 2:3 and that of the height is 5:3, then the ratio of their volume is
a) 27:20 b) 20: 27 c) 4 :9 d) 9 :4
95) 2 right circular cylinders have equal volumes and the ratio of their heights is 1:2, then the ratio of their radii--
a) 1:√2 b) √2: 1 c) 1:2 d) 2:1
96) If the radius of a right circular cylinder is half the length and twice the height, then the volume of the cylinder will be the volume of the initial cylinder.
a) equal b) double c) half d) four times
97) when the radius of a right circular cylinder is doubled and the height is halved , the area of the circle is the area of the original cylinder.
a) equal b) double c) half d) four times.
98) If the ratio of the volumes of two solid sphere is 1:8, then the ratio of the area of the sphere will be ---
a) 1:2 b) 1:4 c) 1: 8 d) 1:16
99) The total surface area of a solid hemisphere of radius 7cm will be
a) 588π sq.cm b) 392π sq.cm c) 147π sq.cm d) 98π sq.cm
100) if the ratio of the areas of the sides of two solid sphere is 16:9, then the ratio of their volumes will be
a) 64 :27 b) 4 :3 c) 27 :64 d) 3:4
101) if the area of the circle of a solid sphere and three times the volume have the same numerical value, then the length of the radius of the sphere is
a) 1 unit b) 2 unit c) 3 units d) 4 units.
102) If the slant height of a right circular cone is 15cm and the diameter of the base is 16cm, then the area of the lateral plane of the cone will be
a) 60π sq.cm b) 68π sq.cm c) 120π sq.cm d) 130 π sq.cm
103) The ratio of the volumes of two right circular cones is 1:4 and the radius of their bases is 4:5 p, then the ratio of their heights will be
a) 1:5 b) 5:4 c) 25:16 d) 25:64
104) Keeping the radius of the base of a right circular cone the same and doubling its height, the increase in its volume will be
a) 100% b) 200% c) 300% d) 400%
105) if the radius of a right circular cone is r/2 units and the slant height is 21 units , then the area of the total plane of the cone is
a) 2πr(l+ r) cu. unit
b) πr(l+ r/4) cu. unit
c) πr(l+ r) cu. unit
d) 2πr cu. unit
106) The median of the data 11 , 29, 17, 21, 13, 31, 39, 19 is
a) (19+29)/2 b) 19 c) 21 d) none
107) Mode is the
a) least frequent value
b) middle most value
c) most frequent value
d) largest value
108) The mode of the data 1, 2, 3, 4, 5, 6, 7 is
a) 4 b) 6 c) 7 d) none
109) median of a frequency distribution can be obtained from
a) pie diagram
b) histogram
c) frequency polygon
d) ogive
110) The median of 1, 5, 9, 3, 8, 7 is
a) 5 b) 7 c) 8 d) 5 and 7 both
111) if the median after arranging in ascending order the data 8, 9, 12, 17, x+ 2, x + 4, 30, 31, 34, 39 is 15, then the value of x is
a) 22 b) 21 c) 20 d) 24
4/10/24
FILL IN THE BLANKS
1) Shyam invests Rs500 for 9 months in a business and David invests Rs600 for 5 months in the same business, the ratio of their profits will be ____.
2) A person deposited Rs100 in a bank and gets the amount Rs121 after 2 years. The rate of compound interest is____%.
3) If the simple interest of a simple for n years at r% p.a. be Rs PNR/25, then the principle will be Rs____.
4) At same rate percent per annum, the simple interest and compound interest of same principal are same in ____ year.
5) A person depreciates at a certain rate over time is called____.
6) A common businesses is of_____type.
7) Barring any other condition, if the partners in a shared business invest the same principal amount for the same period of time, it is called a ____ Shared business.
8) Barring any other condition, when the partners in the business invest the principal amount at different times, it is called____. Shared business.
9) The person who gives loan is called____.
10) Amount of Rs2P per t years at the rate of simple interest r/2% per annum (2P+ ____) Rs.
11) if the ratio of principle and amount for 1 year is 8:9, then the rate of the simple interest per annum is_____.
12) Fixed amount rupee fixed annual interest rate one year compound interest rate and simple interest rate ____.
13) With the passage of time, someone grows at a certain rate , it is called___.
14) The roots of the quadric equation ax²+ 2bx + c=____(a≠0) are real and equal, then b²= _____.
15) if the product and sum of two quadratic surfs is a rational number, then the surds are_____ surd.
16) The equation (a- 2)x²+ 3x +5=0 will not be a quadratic equation for a=___.
17) In in quadratic equation ax²+ bx + c=0(a≠ 0), b²= 4ac, then the roots of the equation will be real and ____.
18) a: 2= b :5 = c: 8 then , a 50%= b 20% = c_____%.
19) if the sum and product of two quadratic conditions is a fundamental number, then both the conditions are____.
20) (x -2) and (x -3) is proportional x to the mean of the x____.
21) (√3- 5) The complement of surds is ____.
22) 5√11 A ____is a number.
23) 7x²- 12x +18=0. The ratio of the sum and the product of the roots of the equations_____.
24) ax²+ bx + c=0 (a≠0) if both the roots of the equation are mutually inverse (reciprocal), then c=____.
25) ax²+ bx + c=0 (a≠ 0) if both the roots of the are mutually inverse and negative, then a+ c=____.
26) The product of three consecutive proportional positive numbers is 64, the proportional between them is ____.
27) If sum of two angles is ___, then they are called supplementary angles.
28) If the bases of two triangles are situated on same line and the other vertex of the two triangles are common, then the ratio of the areas of two triangles are ____ to the ratio of their bases.
29) if ABCD is a cyclic parallelogram then angle A is____.
30) If the length of the sides of two Triangles are in proportion, then two Triangles are _____.
31) If both the angles made by an arc in the same arc are equal, then the length of both the arcs is ____.
32) A contagious Parallelogram is a_____.
33) The vertices of a square figure are ____.
34) If a straight line intersects a cut at two points, then the straight line is called the ___ of the cut.
35) Due to the ratio of the length of the two chords PQ and RS in the O central circle, 1:1 angle POQ: angle ROS= ____ .
36) the perpendicular bisector of a chord of a chord is____.
37) Angles lying in the same verse are ____.
38) If the line segment joining two points makes equal opposite angles to the other two points on the same side, then the four points will be____.
39) Two Triangles are similar if their____
40) If a straight line intersects the circle at two points, then the straight line is called ____ of circle.
41) Two circles touch each other externally at the point A. A common tangent drawn to the two circles at the point A is ____ common tangent (direct/ transverse).
42) if AOB is the diameter of a circle and C and D are two different points on the circumference not on the same side of AB, such that angle AOC=130°, then the value of angle CDB will be____.
43) The line segment parallel to any side of a triangle divides other two sides or the extended two sides ___.
44) The perpendicular bisector of any chord of a circle is____ of that circle.
45) The angle in the segment of a circle which is less than the semicircle is an ____angle.
46) three circles can intersect each other at more than ____point/s.
47) The distance between the centres of two circles with radii 9cm and 16cm is 25cm. The length of the segment of the tangent between them is____cm.
48) In ∆ ABC , angle A= angle B= 60°, AC=8cm. The lines AD and BD intersect at D with D= 90°. If DB= 2cm then the length of AD is ____cm.
49) If an exterior angle of a cyclic quadrilateral be 50°, then the interior opposite angle is____.
50) If PQ is the diameter of a circle with centre O and R is a point on the circumference such that angle ROQ= 120°, then the value of angle ORP is ____.
51) The circle drawn with the hypotenuse of a right angled triangle as diameter passes through the ____.
52) The straight lines parallel to the parallel sides of a trapezium divides____ other two sides.
53) The simplest value of cos53°/sin37° is _____.
54) if tan35° tan55°= sinx, then lowest positive value of x will be_____.
55) If cos²x - sin²x = 1/x (x > 1), then cos⁴x - sin⁴x = ____.
56) The circular value of the supplementary angle of the measure 3π/8 is___.
57) The value of (sin 12 . cos 18. sec 78. Cosec72) is___.
58) If the sun's angle of elevation increases from 30° to 60°, the length of the shadow of a post____. (decreases/ increases).
59) if the angle of elevation of the sun is 45°, then the length of shadow and length of post ate____.
60) The value of tan 15 tan 45 tan 60 tan 75 is ____.
61) if tanx = 4/5, then x = ____.
62) If sinx =1/2, then cos2x =_____.
63) If the opposite angles of a quadrilateral be supplement then the vertices of the quadrilateral will be_____.
64) cosx= √3/2, then sin2x=_____.
65) The value of (4/sec²x + 1/(1+ cot²x) + 3 sin²x) is ____.
66) The vertical of a cyclic squares are _____.
67) If sinx =1/2, then tan2x =___.
68) If sin(x - 30°)= 1/2, then the value of cosx is_____.
69) π radian is a _____ angle.
70) One solid sphere is melted and a solid right circular cylinder is made, then _____ of sphere and the cylinder will be equal.
71) number of surfaces of the solid right circular cylinder is____.
72) The shape of a pencil with one end sarpend is the combination of a cylinder and a ____.
73) The numbers are plane surface of a solid hemisphere are____.
74) ABC is the hypotenuse of the right angle AC triangle. Considering the side AB as an axis, the diameter of the right circular cone that will be formed in full circle of the triangle will be____.
75) if the volume of a right circular cone is V cubic units and the area of the base being A square units, the height will be_____.
76) If the radius of the base of a right circular cylinder and a right circular cone are the same and their heights are also be same, then the ratio of their volumes will be ____.
77) A solid sphere is melted to form a solid right circular cylinder. The volume of the sphere and the cylinder is____.
78) The number of diagonals of a rectangular solid is____.
79) The length of the diagonal of a plane of a cube= ____ x length of one side.
80) A rectangular paper has unit length and unit width . A rectangular paper is folded into cylinder whose circumference is equal to the length of the paper____ curve of cylinder.
81) The length of the radius of the base of a solid right circular cylinder and two hemisphere are equal. If tor hemisphere are placed side by side with the plane of the cylinder, then what is the shape of the new solid object = area of the plane of a hemisphere + ____ area of the curve of+ The area of the curve of second hemisphere.
82) If the diameter of a circular pipe is 3 cm and height is 4cm, then the length of the longest pole that will be placed inside the pipe is_____ cm.
83) If the volume of a right circular cylinder and the area of the curved plane have the same number of values, then the length of the diameter of the cylinder is____.
84) The variable x₁, x₂,.......x₁₀₀ are in ascending order of their magnitude, then the median of the variable is____.
85) The measured of central tendency are mean, median and____.
86) if the mean x₁, x₂, x₃....xₙ be bar x, then the mean of kx₁, kx₂, kx₃....kxₙ is _____(k≠0).
87) The median of the data 8, 9, 6, 7, 5, 6, 7, 8, 9, 10 is____.
88) If the mean of the number 6, 7, x, 8, y, 14 is 9, then x + y=____.
89) The relation between x and y is 2x + 3y=7. If the median of y is 2; then the median of x is _____.
90) The median of 2, 3, 4, 3, 6, 7, 8 is ____.
91) The following are the marks obtained by 10 students in physics test: 65, 52, 71, 47, 49, 51, 37, 29, 77, 62; then the mean mark is____.
92) The mode of 2, 3, 5, 6, 2, 4, 2, 8, 6, 9 will be____.
93) The mode of the data 1,1,2,2,2,3,3,3,4,4,5,6,7 is____.
CHOOSE THE CORRECT OPTION:
1) if a principal becomes twice of it in 10 years, then the rate of a simple interest for annum is
a) 5% b) 10% c) 15% d) 20%.
2) In a partnership business , the ratio of share of profit of two friends is 1/2: 13, then the ratio of their principal is
a) 2:3 b) 32 c) 1:1 d) 5:3
3) Interest on Rs a at the simple interest 10% per annum for b months is
a) ab/100 b) ab/120 c) ab/1200 c) ab/10.
4) If the ratio of principal
and yearly amounts be in the ratio 25:28, then the yearly rate of interest is
a) 3% b) 12% c) 75/7% d) 8%
5) If the total interest becomes Rsx for any principal having the rate of simple interest of x% per annum for x years then the principal will be
a) Rsx b) Rs 100x c) Rs 100/x d) Rs 100/x²
6) The total interest of a principal in n years, at the rate of simple interest of r% per annum is one/109, the principle will be
a) Rs2p b) Rs4p c) Rs3p d) 5p.
7) If the interest on Rs p at the rate of simple interest of r% per annum in t years is I, then
a) I= prt b) prt I= 100. I c) prt = 100. I d) none.
8) A principal becomes twice of its amount in 20 years at a certain rate of simple interest. At that same rate of simple interest, that principal becomes thrice of its amount in
a) 30 years b) 35 years c) 40 years d) 45 years
9) A sum of Rs400 amounts to Rs480 in 4 years. What will it amount to if the rate of interest is increased by 2% ?
a) Rs484 b) Rs560 c) Rs512 d) none
10) At what rate of percent per annum will Rs2304 amount to Rs2500 in 2 years at compound interest ?
a) 9/2% b) 21/5% c) 25/6% d) 13/3%
11) An amount doubles itself in 5 years with simple interest. What is the amount of interest percent per annum?
a) 10% b) 20% c) 25% d) 30%
12) Three partners in a business in the ratio 5:7:8, they had partnered for 14 months, 8 months and 7 months respectively. What is the ratio of their investments ?
a) 5:7:8 b) 20:49: 64 c) 38 :28 :21 d) none
13) A person deposited Rs109 in a bank and got the amount Rs121 for 2 years. The rate of compound interest is
a) 10% b) 20% c) 5% d) 21/2%
14) In case of compound interest, the rate of compound interest per annum is
a) equal b) unequal c) both equal or unequal d) none.
15) In case of compound interest
a) The principals remains unchanged each year
b) principal changes in each year
c) principal may be equal or unequal in each year d) none
16) The capital of 3 friends in a partnership business are Rs200, Rs 150 and Rs250 respectively. After some time the ratio of their profit share will be
a) 5:3:4 b) 4:3:5 c) 3: 4:5 d) 5:4:3
17) Suvendu and Nitin started business with capitals of Rs1500 and Rs1000. After a year there was a loss of Rs75, then the loss of suvendu is
a) Rs45 b) Rs30 c) Rs25 d) Rs40
18) Amal and Bimal started a business. Amal invested Rs500 for 9 months and Bimal invested some money for 6 months. They make a profit of Rs69 in a year and Bimal gets profits share of Rs46. The capital of Bimal in the business is
a) Rs1500 b) Rs3000 c) Rs4500 d) Rs6000
19) Pallavi invested Rs500 for 9 months and Raja invested Rs600 for 5 months in a business. The ratio of their profit shares will be
a) 3:2 b) 5:6 c) 6:5 d) 9:5
20) The product of two roots of the equation x²-7x +3 =0 is
a) 7 b) -7 c) 3 d) - 3
21) If p + q= √13 and p- q= √5 then the value of PQ is
a) 2 b) 18 c) 9 d) 8
22) If x ∞ y, then
a) x³∞ y³ b) x²∞ y² c) x ∞ y³ d) x²∞ y
23) Under what condition one root of the quadric equation ax²+ bx + c=0 is zero ?
a) a= 0 b) b= 0 c) c= 0 d) none.
24) 2x²- 3x - k +2=0 one root of the equation is 0. The value of k is
a) 2 b) -2 c) 1/2 d) -1/2
25) If a/b = b/4 = c/7 then, the value of (a+ b+ c)/c
a) 1 b) 2 c) 3 d) 4
26) The mean proportional of 9 and 25 is
a) 20 b) 21 c) 41 d) 441
27) If a + b= √5 and a - b=√3 then the value of a²+ b²
a) 8 b) 4 c) 2 d) 1
28) If two roots of equation x²+ 4x +k=0 are equal, then the value of k is
a) 1 b) 2 c) 3 d) 4
29) If two roots of equation x²- 6x + k=0 are real and unequal then what is the value of k ?
a) more than 6 b) less than 6 c) more than 9 d) less than 9.
30) The sum of two roots of the equation x²- 6x +2=0
a) 2 b) - 2 c) 6 d) - 6
31) If the product of two roots of the equation is x²- 3x + k=10 is -2, what is the value of k ?
a) - 2 b) - 8 c) 8 d) 12
32) If two roots of the equation ax²+ bx + c=0(a≠ 0) be equal , then
a) c= -b/2a b) c= b/2a c) c= - b²/4a d) c= b²/4a
33) The roots of the equation x²= 6² is/are
a) 0 b) 6 c) 0 and 6 d) - 6
34) if two roots of the equation (k +1)x²+ 2kx + (k +2)= 0 are equal and negative then the value of k is
a) 1 b) -1 c) 0 d) -2
35) If the roots of the equation ax²+ bx + c=0(c ≠ 0) are real and unequal then b²- 4ax will be
a) >0 b) =0 c) <0 d) none.
36) The number of roots in a quadratic equation is
a) 1 b) 2 c) 3 d) none.
37) If ax²+ bx + c=0 is a quadratic equation then
a) b≠ 0 b) c≠ 0 c) a≠ 0 d) none.
38) The highest power of the variable of a quadratic equation is
a) 1 b) 2 c) 3 d) none
39) The equation 4(5x²- 7x +2)= 5(4x²- 6x +3) is
a) linear b) quadratic c) 3rd degree d) none
40) Rthird proportion of 8 and 12 is
a) 12 b) 16 c) 18 d) 20
41) a is a positive number and if a: 27/64 = 3/4: a, then the value of a is :
a) 81/256 b) 9 c) 9/16 d) 16/9
42) 2a = 3b = 4c then value of a :b :c is
a) 3:4:6 b) 4: 3: 6 c) 3:6:4 d) 6:4:3
43) x = 2+ √3 then value of x+ 1/x
a) 2 b) 2√3 c) 4 d) 2-√3
44) Decreasing will result in failure of √125 to √5
a) √80 b) √120 c) √100 d) none
45) will be multiplied by (5- √3)(√3- 1)(5+ √3)(√3 +1)
a) 22 b) 44 c) 2 d) 11
46) x ∞ y and y= 4 when x= 8; x = 32 then, positive value of y
a) 4 b) 8 c) 16 d) 32
47) if y - z ∞ 1/x , z - x ∞ 1/y and x - y ∞ 1/z then, the sum of the three change constants will be.
a) 0 b) 1 c) -1 d) 2
48) x ∞ 1/y then
a) x= 1/y b) y= 1/x c) xy =1 d) xy = constant
49) x ∞ y and y=8 when x= 2, if y= 16 then the value of x is
a) 2 b) 4 c) 6 d) 8
50) If x ∞ y and y ∞ z then
a) z∞x b) x ∞yz c) x ∞ y/z d) z ∞ xy
51) The length of the two chords AB and CD cycle of a circle of centre O are equal and angle AOB= 60°,then angle COD= is
a) 40° b) 30° c) 60° d) 90°
52) O is the centre of a circle and AB is a diameter, ABCD is a the cyclic quadrilateral.Angle ABC=65°, angle DAC= 40°, then the measure of angle BCD is
a) 75° b) 105° c) 115° d) 80°
53) If Angle A =100° of a cyclic quadrilateral ABCD, then the value of angle C is
a) 50° b) 80° c) 180° d) 200°
54) The number of common tangents of two circles when they do not touch or intersect each other is :
a) 2 b) 1 c) 3 d) 2
55) The length of the radius of 6 circle is 13cm and the length of a chord of the circle is 10cm, the distance of the coord from the centre of the circle is
a) 12.5cm b) 12 cm c) √69cm d) 24 cm
56) The centre of two concentric circles is O; a straight line intersects a circle at point A and B and the other circle at point C and D. If AC= 5 cm, then the length of BD is
a) 2.5cm b) 5cm c) 10 cm d) none.
57) The distance between two parallel chords of length 8cm each in a circle of diameter 10 cm is
a) 6cm b) 7cm c) 8cm d) 5.5 cm
a) 70° b) 60° c) 40° d) 200°
59) In the adjoining figure,if O is the centre of the circle and the BC is the diameter then the value of x is
a) 60° b) 50° c) 100° d) 80°
60) In the adjoining figure,O is the centre of the circle; if ang ACB =30°, angle ABC= 60°, angle DAB= 35° and DBX= x°, then the value of x is
a) 35 b) 70 c) 65 d) 55
61) If AB is a diameter of a circle with Centre O and C is a point on the circumference such that angle BOC=60°, then the value of angle AOC is
a) 60° b) 30° c) 120° d) 90°
62) In the adjoining figure,O is the centre of the circle and AB is the diameter. If AB || CD, angle ABC=25°, then the value of angle CED is
a) 80° b) 50° c) 25° d) 40°
63) A person goes 24m West from a place and then he goes 10m north. The distance of the person from the starting point is
a) 34m b) 17m c) 26m d) 25m
64) Two rods of 13m length and 7m length are situated perpendicularly on the ground and the distance between their feet is 8m. The distance between their top parts is
a) 9m b) 10m c) 11m d) 12m.
65) In the adjoining figure,O is the centre of the circle, id angle BCD= 28°, angle AEC= 38°, then the value of angle AXB= ?
a) 56° b) 86° c) 38° d) 28°
66) In the diagrambesides O is the centre of the circle and AB is a diameter. ABCD is a cyclic quadrilateral. Angle BAC is
a) 50° b) 60° c) 30° d) 40°
67) In the diagrambesides ABCD is a cyclic quadrilateral. BA is produced to the point F. If AE|| CD, angle ABC= 92° and angle FAE= 20°, then the value of angle BCD is
a) 20° b) 88° c) 108° d) 72°
68) I is the centre of ∆ ABC, angle ABC= 60° and angle ACB= 50°. Then angle BIC is
a) 55° b) 125° c) 70° d) 65°
69) In the adjoining figure,O is the centre of the cirle, if Angle BAD= 65°, angle BCD= 45°, then the value of angle BCD is
a) 65° b) 45° c) 40° d) 20°
70) If sinx - cosx = 0 (0≤ x ≤ 90°) and sex + cosecx = y, then the value of y is
a) 1 b) 2 c) √2 d) 2√2
71) If tanx + cotx =2, then the value of (tan¹³x + cot¹³x) is
a) 1 b) 0 c) 2 d) none
72) If cotx = 7/7.5, then cosecx is
a) 7.5/4 b) 8/17 c) 17/15 d) 15/17
73) If 2x = secA and tanA= 2/x then the value of 2(x²- 1/x²)²= ?
a) 1/2 b) 1/4 c) 1/8 d) 1/16
74) The value of (sin43° . cos47°+ cos43° sin47°) is
a) 0 b) 1 c) sun4° d) cos4°
75) If tanx = 4/5, then cosx =
a) 4/5 b) 3/5 c) 3/4 d) 5/√41
76) If sinx = 1/√2, then sec2x =
a) 0 b) 1 c) 2 d) none
77) The circular measure of an angle of an isosceles triangle is 5π/9, the circular measure of one of the other angles must be---
a) 5π/18 b) 5π/9 c) 2π/9 d) 4π/9
78) The value of ( tan35/cot55 + cot78/tan12) is
a) 0 b) 1 c) 2 d) none
79) ABC is a triangle. Then sin{(B+ C)/2}=
a) sin(A/2) b) cos(A/2) c) sinA d) cosA
80) Height of tower is 100√3 metres. The angle of elevation of the top of the tower from a point at a distance 100metres from the foot of the tower is
a) 30° b) 45° c) 60° d) none
81) The end point of the minute hand of a clock rotates in 1 hour.
a) π/4 radian b) π.2 radian c) π radian d) 2π radian
82) The measurement of x in relation to s= rx is determined by
a) sexagesimal system
b) circular system
c) both of these d) none
83) If the ratio of the volume of two right circular cones is 1:4 and the ratio of radii of their bases is 4:5, then the ratio of their height is:
a) 1:5 b) 5:4 c) 25: 16 d) 25 :64
84) If two cubes of length of each side 2√6 are placed side by side, then the length of the diagonal of the cuboid so produce is
a) 10cm b) 6cm c) 2cm d) 12cm
85) If side of a cube is a unit and the diagonal of the cube is d unit then the relation between a and d will be:
a) √2 a= d b) √3 a = d c) a= √3 d d) a= √2 d
86) If each of radius of the base and height of a cone be doubled, then the volume of it will be
a) 3 times b) 4 times c) 6 times d) 8 times
87) If the height of a cone is h unit, slant height I units and the diameter of the base is d unit, then (l²- h²)/d²= ?
a) 1/2 b) 1/3 c) 1/4 d) 1/5
88) The volume inside a rectangular box is 440 cubic cm and the area of the inner base is 88 sq cm, then the inner height of the box is
a) 4cm b) 5cm c) 3cm d) 6 cm
89) A rectangular pit is 40m long , 12m wide and 16m deep. In this pit a plank 5m long, 4 m wide and 2 m high will be placed ?
a) 190 b) 192 c) 184 d) 180
90) The area of the lateral plane of a cube is 256 sq.m volume of cube
a) 64cune m b) 216 cube m c) 256 cube m d) 51 cube m
91) If the ratio of the volumes of two cubes is 1:27, then the ratio of the area of the total surface of both the cubes is
a) 1:3 b) 1 : 8 c) 1: 9 d) 1:18
92) if the area of all the sides of a cube is 5 square unit and the length of the diagonal is d units, then the contact between S and d is
a) S= 6d² b) 3S= 7d c) S³= d² d) d²= S/2
93) If the ratio of the radii of two circular solid cylinder 2 :3 and the ratio of their height is 5:3, then the ratio of the areas of their sides is
a) 2:5 b) 8 : 7 c) 10:9 d) 16:9
94) if the ratio of the radiu of two right circular solid cylinder is 2:3 and that of the height is 5:3, then the ratio of their volume is
a) 27:20 b) 20: 27 c) 4 :9 d) 9 :4
95) 2 right circular cylinders have equal volumes and the ratio of their heights is 1:2, then the ratio of their radii--
a) 1:√2 b) √2: 1 c) 1:2 d) 2:1
96) If the radius of a right circular cylinder is half the length and twice the height, then the volume of the cylinder will be the volume of the initial cylinder.
a) equal b) double c) half d) four times
97) when the radius of a right circular cylinder is doubled and the height is halved , the area of the circle is the area of the original cylinder.
a) equal b) double c) half d) four times.
98) If the ratio of the volumes of two solid sphere is 1:8, then the ratio of the area of the sphere will be ---
a) 1:2 b) 1:4 c) 1: 8 d) 1:16
99) The total surface area of a solid hemisphere of radius 7cm will be
a) 588π sq.cm b) 392π sq.cm c) 147π sq.cm d) 98π sq.cm
100) if the ratio of the areas of the sides of two solid sphere is 16:9, then the ratio of their volumes will be
a) 64 :27 b) 4 :3 c) 27 :64 d) 3:4
101) if the area of the circle of a solid sphere and three times the volume have the same numerical value, then the length of the radius of the sphere is
a) 1 unit b) 2 unit c) 3 units d) 4 units.
102) If the slant height of a right circular cone is 15cm and the diameter of the base is 16cm, then the area of the lateral plane of the cone will be
a) 60π sq.cm b) 68π sq.cm c) 120π sq.cm d) 130 π sq.cm
103) The ratio of the volumes of two right circular cones is 1:4 and the radius of their bases is 4:5 p, then the ratio of their heights will be
a) 1:5 b) 5:4 c) 25:16 d) 25:64
104) Keeping the radius of the base of a right circular cone the same and doubling its height, the increase in its volume will be
a) 100% b) 200% c) 300% d) 400%
105) if the radius of a right circular cone is r/2 units and the slant height is 21 units , then the area of the total plane of the cone is
a) 2πr(l+ r) cu. unit
b) πr(l+ r/4) cu. unit
c) πr(l+ r) cu. unit
d) 2πr cu. unit
106) The median of the data 11 , 29, 17, 21, 13, 31, 39, 19 is
a) (19+29)/2 b) 19 c) 21 d) none
107) Mode is the
a) least frequent value
b) middle most value
c) most frequent value
d) largest value
108) The mode of the data 1, 2, 3, 4, 5, 6, 7 is
a) 4 b) 6 c) 7 d) none
109) median of a frequency distribution can be obtained from
a) pie diagram
b) histogram
c) frequency polygon
d) ogive
110) The median of 1, 5, 9, 3, 8, 7 is
a) 5 b) 7 c) 8 d) 5 and 7 both
111) if the median after arranging in ascending order the data 8, 9, 12, 17, x+ 2, x + 4, 30, 31, 34, 39 is 15, then the value of x is
a) 22 b) 21 c) 20 d) 24
Day- 8
1) Solve: √(3x²+ x+5}= x - 3. -4,1/2
2) Roots of the quadric equation are 1/2 and -14. Find the equation. 2x²+ 27x -14= 0
3) 8(t²+ 1/t²)- 42(t - 1/t)+ 29= 0. Find the possible values of t. 15/4,3/2
4) Solve : x²- 6x -15= 0. Give your answer correct to two decimal places. -1.90, 7,9
5) Solve the following:
a) 6x²- x = 35.
b) x² - 8X - 1280 = 0.
c) 1/(2y -9) = 1/(y -3) + 4/5.
d) 2x²+ 11x -10 = 0. Give your answer correct to two decimal places.
e) 5ˣ⁺¹ + 5²⁻ˣ =126.
1) A two digit number is such that the product of digits is 12. When 9 is added to the number the digits are interchanged. Find the number.
2) The sides of a right angle triangle are x cm, 4(x + 1)cm, and (4 x + 5)cm. Find x.
3) A man purchased sheep for Rs4500. Three sheep were lost and the rest he sold for Rs30 more per sheep than he had paid. if his gain on the whole transaction is 8%, how many sheep did he buy ?
4) The sum of the ages of a man and his son is 46 years and the product of their ages is 168 years. Find the age of the son.
5) The total surface area of a cylinder is 75.24 cm² and its height is 3.6 cm. if its radius is x cm, find x.
6) The bill of a party for a certain number of people is Rs19200. If there were 10 more persons, the bill each person had to pay would have reduced by Rs160. Find the number of people at the party. 30
Day- 7 (22/7/24)
1) Calculate the compound interest for the second and third year on Rs20000 invested for 4 years at 10% p.a. 2200, 2420
2) Vijay borrowed Rs5000 and agreed to pay intrest at the rate of 10%, 12% and 14% for the first, second and third year respectively. Find the total amount he had to pay after 3 years. Rs7022.40
3) The machinery of a certain factory is valued at Rs550000. It depreciates each year at 10% of its value. Find the value of the machinery at the end of 3 years. 400950
4) A certain sum money invested at compound interest amounts to Rs2420 at the end of second year and Rs2662 at the end of third year. 10%, 2000
5) At what rate percent per annum, compound interest , will Rs3000 amount to Rs3370.80 in two years ? 6%
6) In how many years will Rs8000 amount to Rs10648 at 10% per annum CI ? 3yrs
7) The difference between simple interest and compound interest is Rs19.20 for 2 years. If the principal is Rs3000, find the rate of interest. 8%
8) A sum of money is invested at compound interest payable. The interest in two successive years is Rs225 and Rs240. Find the rate of interest. 20/3%
9) The compound interest for the 3rd on a certain sum is Rs726. If the simple interest on the same sum is Rs1800, find the rate and the sum. 10%, Rs6000
10) Saurav borrowed a certain sum of money and paid it back in 2 years in two equal installments. If the rate of compound interest was 4% per annum and if he paid back Rs4056 annually, what sum did he borrow ? Rs7650
(3/6/24)
A) Solve for x:
1) {√(x+2)+
√(x -3)}/{√(x+2)- √(x -3)} = 5.
2) {√(x+5)+ √(x -16)}/{√(x+5)- √(x -16)} = 7/3.
3) {√(7x)+ √(4x -3)}/{√(7x)- √(4x -3)} = 6.
4) 16{(a - x)/(a+ x)}³= (a+ x)/(a- x).
5) (x²+ 5x)/(3x²+1)= 14/13.
6) (3x²+ 5x +8)/(5x²+ 6x +12)= (3x +5)/(5x +6).
7) {√(x+a)+ √(x -b)}/{√(x+a)- √(x -b)} = (a + b)/(a- b).
8) {√(3x+7)+ √(3x)}/{√(3x+7)- √(3x)} = 7.
9) {√(5)+ √(5 - x)}/{√(5)- √(5 - x)} = 3.
10) (1- px)/(1+ px) . √{(1- qx)/(1+ qx)}= 1.
11) (a + √(a²- 2ax))/(a - √(a²- 2ax))= b.
12) If x= 2ab/(a+ b), a≠ b, find the value of (x+ a)/(x - a)+ (x +b)/(x - b).
13) If x= 4√6/(√2+ √3), find the value of (x+ 2√2)/(x - 2√2) + (x+ 2√3)/(x - 2√3).
14) If x= 6pq/p+ q), find the value of (x + 3p)/(x - 3p) + (x + 3q)/(x - 3q).
15) If p= 4xy/(x + y) find the value of (p+ 2x)/(p - 2x) = (p + 2y)/(p - 2y).
B) 1) a) Show that 3ax²- 2bx + 3a = 0 when x= {√(b +3a)+ √(b -3a)}/{√(b+3a)- √(b -3à)}.
b) Show that 3nx²- 2mx + 3n = 0 when x= {√(m +3n)+ √(m -3n)}/{√(m+3n)- √(m -3n)}.
2)a) If a+ c = 2b and 1/a + 1/d = 2/c, show that a: b:: c: d.
b) (4a + 7b)/(4a - 7b)= (4c + 7d)/(4c - 7d) then show that a/b = c/d.
3) If (a²+ b²)(m²+ n²)= (am + bn)², show a/m = b/n.
4) If x/b = y/b = z/c show that
a) x³/a³ - y³/b³ + z³/c³ = xyz/abc.
b) ³√{(lx⁻³ + my⁻³ + nz⁻³)/(la⁻³ + mb⁻³ + nc⁻³)}⁻¹
5) If y= {(p +1)¹⁾³ + (p -1)¹⁾³}/{(p +1)¹⁾³ - (p -1)¹⁾³} find the value of y³- 3py²+ 3y - p.
6) (ay - bx)/c = (CX - az)/b = (bz - cy)/a, show that x/a = y/b = z/c.
7) If ax = by = cz, show that x²/yz + y²/zx + z²/xy = bc/a² + ca/b² + ab/c²
8) x/{(b -c)(b + c - 2a)}= y/{(c - a)(c + a - 2b)}= z/{(a - b)(a+ b - 2c)} show that x + y + z= 0.
9) If (by + cz)/(b²+ c²)= (cz + ax)/(c²+ a²)= (ax + by)/(a²+ b²), then show that each ratio is equal to x/a = y/b = z/c.
10) Show: {(a- b)/c + (a- c)/b}² - {(d - b)/c + (d - c)/b}²= (a - d)²(1/c² - 1/b²).
11) If (b + c - a)/(y + z - x) = (c + a - b)/(z + x - y)= (a + b - c)/(x + y - z), then each of the ratio is equal to a/b = b/y = c/z.
12) If (a²+ c²)/(ab + CD) = (ab + cd)/(b²+ d²), then show that a/b = c/d.
C) If a/b = c/d = e/f, show that each of these is equal to:
1) (a + 3c- 5e)/(b + 3d - 5f)
2) {(a³- 2c³+ 3e³)/(b³- 2d³+ 3f³)}¹⁾³
3) {(a²+ c²+ e²)/(b²+ a²+ f²)}¹⁾²
4) (5a + 6b)/(5a - 6b)= (5c +6d)/(5c - 6d).
5) (a+ c +e)/(b + d+ f).
6) (a³+ c³+ e³)/(b³+ d³+ f³)= ace/bdf.
7) (a²b²+ c²d²+ e²f²)/(ab³+ cd³+ ef³)}³⁾²= √(ace/bdf).
8) Each ratio= √{(3a²+ 5c²- 7e²)/(3b²+ 5d²- 7f²)}.
9) (b²+ d²+ f²)(a²+ c²+ e²)= (ab + cd+ ef)².
10) (ab+cd + ef)²=(a²+ c²+ e²)(b²+ d²+ f²).
D) 1) If 8a + 9b : 8c + 9d :: 8a - 9b : 8c - 9d show that a, b, c, d are in proportion.
2) If a: b:: c: d show that (4a + 5b):(4a - 5b):: (4c + 5d): (4c - 5d).
3) If (2mc + 6mb + 3nc + 9nd)(2ma - 6mb - 3nc + 9nd)= (2ma - 6mb + 3nc - 9nd) (2ma + 6mb - 3nc - 9nd) then show that a, b, c,d are in proportional
4) If a, b, c are in continued proportion then prove
a) (a + b + c)(a - b - c)= a²+ b²+ c²
b) (a+ b + c)²/(a²+ b²+ c²)= (a+ b + c)/(a - b + c).
c) (a + b + c)(a - b+ c)= a²+ b²+ c²
d) (a+ b): (b + c):: a²(b - c): b²(a - b).
5) If a: b :: c: d, prove that
a) a+ b : c+ d :: √(a²+ b²): √(c²+ d²).
6) If a, b, c , d are in proportion, then prove that
a) a³+ c³+ e³: b³+ d³+ f³:: ace: bdf.
b) 4(a+ b)(c +d)= bd{(a+ b)/b + (c +d)/d}²
c) (ab + cd)²= (a²+ c²)(b²+ d²)
d) a: d :: (pa³+ qb³+ rc³): (pb³+ qc³+ rd³).
e) (a - b): (a + b):: (a - d): (a + 2b + 2c + d).
f) (b - c)²+ (c - a)²+ (d - b)²= (a - d)²
7) If a/b = b/c = c/d then show that
a) √{(a+ b+ c)(b+ c+ d)}/{√(ab)+ √(bc) + √(cd)}= 1
b) (a²+ b²+ c²)(b²+ c²+ d²)= (ab + bc + CD)²
c) a/d = (a - b)³/(b - c)³.
8) If a/b = c/d, show √{(a+ b + c)(b + c + d)}= √{(ab) + √(bc)+ √(cd)}.
9) If p/q = r/s , show that (2p + 3q)/(2p - 3q) = (2r + 3s)/(2r - 3s
Day- 5 (17/5/24)
1) 2x²+ 3x-20= 0
2) 4x² - 12x + 9= 0.
3) 3x² -8x + 2= 0.
4) 2x + 2/x +5= 0
5) x + 96/x = 22.
6) x(2x +5) -3= 0
7) x(3x + 1/2) - 6 = 0
8) 3x(3x - 8)+ 16= 0
9) 4(x +2)(x +1)= 15.
10) One root of x² - 3x - c= 0 is -2, find the value of c and the other root.
11) One root of 2x²- 3(5x + c)= 0 is 3/2, find the value of c and other root.
Solve the following equations using formula
Give your answer correct to 2 decimal places.
1) x²+ 4x + 2 = 0.
2) 5x²- 3x- 7= 0.
3) x - 10/x = -7.
4) 2x + 5 = 9/x.
5) 3x(2x -7)= 4.
6) 2(x -1)(x -5)= 5.
7) 5(x +1)²+ 10(x +1)+ 3= 0.
8) (x -1)² -6(x -1)= 11.
9) Find the values of k for which the given equation has real and equal roots:
a) 12x²+ 4kx +3= 0.
b) kx² - 2 √5 x + 4= 0.
c) 4x²- 3kx + 1 = 0.
d) (k+1) x² - 2(k -1)x + 1 = 0.
10) Find the values of k for which the given equation has real roots.
a) 2x² - 5x- k = 0.
b) kx²+ 6x +1 = 0.
Day- 4 (12/5.24)
Solve the following equation:
Type -1
1) 2x²+ 2= 5x.
2) x²+ 9x - 52= 0
3) 6x²+ 5x - 4= 0.
4) 3x²+ 14x +8= 0
5) 7x²= 8 - 10x.
6) x(x +1)+ (x +2)(x +3)= 42.
7) 6x(3x -7)= 7(7- 3x).
8) 3(x²- 4)= 5x.
9) √3 x²+ 10x + 7 √3 = 0.
10) x²+ 2 √2 x - 6= 0
Type - 2
1) (x +3)/(x +2)= (3x -7)/(2x -3).
2) (x +2)/(x +3)= (2x -3)/(3x -7).
3) (5x +1)/(7x +5)= (3x +1)/(7x +1).
4) (3x -7)/(2x -5)= (x +1)/(x -1).
5) (x +1)/(x - 2)+ (x +11)/(x +3)= 4.
6) x/(x +1)+ (x +1)/x = 34/15, x≠ 0, x≠ -1
7) 6/(x +1 )+ 5/(2x +1)= 3
8) 4/(x -1)- 5/(x +2)= 3/x.
9) 5/(x -2)- 4/x = 3//(x +6).
10) (x +2)/6 - 1/(x +2)= 1/6.
11) x⁴- 10x² + 9= 0
12) x⁴- 25x² + 25= 0
13) 11/(5x -4) - 10/(4 - 5x)= 1
Type -3
1) Find the value of p in the following:
a) If (k+2)= 0 and 4k²+ kp²+ 82= 0.
b) If (2k -1)= 0 and k²+ 8kp²+ 2p= 0.
Type - 4
For each of the following solution set, find the quadric equation:
a) x= 2,3
b) x= 3, -4
c) x = 2, 2
d) x= 1/2, 1/3
Miscellaneous
1) Solve: x - 10/x = 9, if x= (a, b), then find
a) a+ b
b) ab
2) Find solution set of 2x² - 5 x - 3= 0, where x= (α, β). if the above quadratic equation is identical equal to ac²+ bx + c= 0, find a, b and c. Hence show that
a) α+ β = -b/a
b) α β = c/a
3) Find the solution set of 2x - 5/x = 3, x= (α, β). If the above quadratic equation is identical equal to ax² + bx + c= 0, find a, b and c. Hence show that
a) α + β = -b/a
b) α β = c/a
Day- 2( 7/5/24)
1) 4 sin²60° + 3 tan²30° - 8 sin45° cos45°
2) 4 sin45° cos45° - sin²30° + tan²60°
3) 4/tan²60° + 1/cos²30° - sin²45°.
4) 4 cos²60° + 4 tan²45° - sin²30°
5) (cos90° + sinn²30° - sin45°)(sin0° + cos60°sin45°)
6) (sin90° + sin²45° cos45° - tan30°)(4sin²30° + cos60° + 1/tan60°)
7) Given cosA = 1/3, A is an acute angle, find tan²A.
8) Given 7 tanA = 24, A is an acute angle, find tan²A.
9) Given 5 tanA = 4, find the value of (5 sinA - 3 cosA)/(5sinA + 2 cosA)
10) Given 5 sinA = 3, A is an acute angle, find (cosA - 1/tanA)/2/tanA.
Day -1
1) If 2 cosx = 2/5, find sinx.
2) Calculate the length of the tangent drawn to a circle of diameter 8cm from a point 5 cm away from the centre of the circle.
3) If x², 4 and 9 are in continued proportion, find the value of x.
4) In the given figure below , AB is a chord of the circle with centre O and BT is tangent to the circle at B. If angle AOB= 32°, find the value of x and y.
5) Solve: 3x²- 5x = 1.
6) Rationalise the denominator: 2/(√5 - 3).
7) In the given figure, find
a) angle APB b) angle AOB
8) Calculate the compound interest on Rs8000 for 1 year at 12% per annum compounded half yearly.
9) Solve: x²- 5x -2= 0
10) If (8a+ 5b)/ (8c + 5d) = (8a- 5b)/ (8c - 5d), show a/b = c/d.
11) If cosA= 4/5 and cosB= 24/25, evaluate
a) cosec²A b) cotA + cotB.
12) The work done by (2x - 3) men in (3x + 1) days and the work done by (3x + 1) men in (x + 8) days are in the ratio 11:15. Find the value of x.
TRIGONOMETRIC IDENTITIES
1) {(1+ tanθ)/(1+ tanθ)}² =
a) 1 b) tan²θ c) tanθ d) 4
2) (sinA - 2 sin³A)/(2cos³A - cosA) is equal to
a) secA b) tanA c) cotA d) 1
3) If tanx = cotx, then
a) x - = 90 b) x= y = 90 c) x + y= 90 d) y - x =90
4) (sec²θ -1)(1- cosec²θ) is equal to
a) -1 b) cotθ c) 0 d) cosecθ
5) √{(secθ -1)/(secθ +1)} + √{(secθ +1)/(secθ -1)} is equal to
a) 2cosecθ b) 2secθ c) 2tanθ d) 2sinθ
6) If sinθ + cosθ = a and secθ + cocosθ =b, then the value of b(a²-1) is
a) 2a b) a+ b c) 2b d) a - b
7) If sinθ + cosθ = √2cosθ, then the value of cosθ - sinθ is
a) √cosθ b) sinθ c) √sinθ d) cosθ
8) cosec²θ/(1 + cot²θ) =
a) 0 b) cosec θ c) 1 d) cotθ
9) sinθ + 2cosθ = 1, then the value of 2sinθ - cosθ =
a) 1 b) 2 c) √2 d) 0
10) If (sinθ + cosθ)(tanθ + cotθ) =
a) secθ + tanθ b) secθ c) secθ + coseθ d) cosecθ
11) sinθ/(1+ cosθ) + (1+ cosθ)/sinθ =
a) 2sinθ b) 2cosθ c) 2tanθ d) 2cosecθ
12) cosθ/(1- sinθ) + cosθ/(1+ sinθ) =
a) 2sinθ b) 2cosθ c) 2 cosecθ d) 2secθ
13) 5 tan²θ - 5 se²θ =
a) 5 b) -5 c) 1/5 d) 0
14) If secθ + tanθ =p, then (p²-1)/(p²+1)=
a) tanθ b) cosθ c) sinθ d) cocosθ
15) sin⁶θ + cos⁶θ + 3sin²θ. cos²θ =
a) 0 b) 1 c) 2 d) -2
16) If sinθ + cosθ = √3, then tanθ + cotθ =
a) 1 b) -1 c) 2 d) -2
17) secθ(1- sinθ)(secθ + tanθ) =
a) 0 b) 1/2 c) 1 d) none
18) 9 sec²θ - 9 tan²θ =
a) 1 b) 9 c) 8 d) 0
19) (1+ tanθ + secθ)(1+ cotθ - cosecθ =
a) 0 b) 1 c) 2 d) -1
20) (1+ tan²θ)/(1+ + cot²θ) =
a) sec²θ b) -1 c) cot²θ d) tan²θ
21) (secθ + tanθ)(1- sinθ =
a) secθ b) sinθ c) cocosθ d) cosθ
22) 2 cos²θ + 2/(1+ cot²θ) =
a) 1 b) 2 c) 0 d) 1/2
23) Simplified form of (3- tanθ)/(3cosecθ - secθ) is
a) cosθ b) sinθ c) cocosθ d) tanθ
SHORT ANSWER TYPE QUESTIONS
Prove the following:
1) secθ/(secθ -1) + secθ/(secθ + 1) = 2cosec²θ.
2) √(sec²θ + cosec²θ) = tanθ + cotθ
3) (cosecθ - sinθ)(secθ - cosθ)(tanθ + cotθ) = 1
4) sinθ/(1+ + cotθ) - cosθ/(1+ tanθ) = sinθ - cosθ
5) sin⁴θ - cos⁴θ = 1- 2cos²θ
6) (1- sinθ)/(1+ sinθ) = (secθ - tanθ)²
7) (sin²x cos²y - cos²x sin²y) = sin²x sin²y.
8) Simplify: (sec²θ - 2 tan²θ)(1- sinθ)(1+ sinθ).
9) For what value of x, 2sin²x - cos²x = 2 ?
10) Find the value: tan²x + cot²x - sec²x cosec²x.
11) sinθ/(cotθ + cosecθ) - sinθ/(cotθ - cosecθ).
LONG ANSWER TYPE QUESTIONS
1) If tanθ + sinθ =m and tanθ - sinθ =n, show that m²- n²= 4 √(mn).
2) Show that: (secθ + tanθ -1)/(tanθ - secθ +1) =(1+ sinθ)/cosθ.
3) If tanθ + secθ = m, then find the value of (m²+1)/2m.
4) Express, a cosθ - b sinθ in terms of a, b and c, where a sinθ + b cosθ = c.
5) Show that: tanθ/(1- cotθ) + cotθ/(1 - tanθ) = tanθ + cotθ+ 1.
6) Show that: (secθ + tanθ -1)(secθ - tanθ +1)/tanθ = 2.
7) If x= a secθ + b tanθ and y= a tanθ + b secθ, then evaluate (a²- b²)/(x²- y²).
8) If x= a secm cos n, y= b secm sin n and z= c tan m, then evaluate x²/a² + y²/b² - z²/c².
8) Show that: 1/(secθ - tanθ) - 1/cosθ - 1/(secθ + tanθ).
9) Show that (1+ cotθ - cosecθ)(1+ tanθ + secθ) = 2.
11/12/24
CONE
R-1
1
) A girl fills a cylindrical bucket 32cm in height and 18cm in radius with sand. She empties the bucket on the ground and makes a conical heap of the sand. If the height of the conical heap is 24cm, find
a) its radius.
b) its slant height (leave your answer in square root form).
2) Water flows at the rate of 10m per minute through a cylindrical pipe 5 mm in diameter. How long would it take to fill a conical vessel whose diameter at the base 40cm and depth 24cm ?
3) An exhibition tent is in the form of the cylinder surmaunted by a cone. The height of the tent above the ground is it 85m and the height of the cylindrical part is 50m. If the diameter of the base is 168m, find the quantity of the Canvas required to make the tent. Allow 20% extra for folds and for stitching. Give your answer to the nearest m².
4) From a solid cylinder whose height 8cm and radius 6cm, a conical cavity of height 8cm and of base radius 6 cm is hollowed out. Find the volume of the remaining solid correct to four significant figures. Also, find the total surface area of the remaining solid.
R-2
1) The base radius and height of a cone are 15cm and 20cm respectively. Find
a) the slant height of the cone. 25cm
b) the curved surface area of the cone.
c) the total surface area of the cone.
d) the volume of the cone.
2) A sector containing an angle of 90° is cut from a circle of radius 42cm and folded into cone. Find the radius and the curved surface area of the cone.
3) The slant height and base radius of a cone are 17cm and 8cm respectively. Find the volume of the cone.
4) The circumference of the base of a cone is 66cm. If its height is 12cm, find the volume of the cone.
5) The curved surface area of a right circular cone is 12320 cm². If the radius of the base is 56cm, find its height.
6) The slant height of a right circular cone is 13cm and its total surface area in 90π cm². Find
a) its radius.
b) its volume in terms of π.
7) two cones have their height in the ratio 1:3 and the radii of their bases in the ratio 3:1. Find the ratio of their volumes.
8) The radius and height of a right circular cone are in the ratio 5:12 and its volume is 2512 cm³. Find the radius and slant height of the cone (use π= 3.14).
9) A sector of radius 35 cm is cut out of a thin cardboard with angle 180°. It is folded into a cone that of maximum size. Find the curved surface area and the volume of the cone.
10) A wooden cone has an outer radius of 60cm and an inner radius of 50cm. The outer and inner heights are 40cm and 36cm respectively. Find the volume of wood in the cone (take π= 3.14).
11) How many metres of Canvas 1.25 m wide will be needed to make a conical tent whose base radius is 17.5m and height 6m ?
12) There are two cones. The curved surface area of one is twice that of the other. The slant height of later is twice that of the former. Find the ratio of their radii.
13) If the radius of the base of a circular cone is halved, keeping the height same. What is the ratio of the volume of the reduced cone to that of the original cone ?
14) The vertical height of a right circular cone is 3 times its diameter and its volume is 54π cm³. Find its height.
15) A conical vessel whose internal radius is 5cm and height is 24cm is full of water. The water is emptied into a cylindrical vessel with internal radius 10cm. Find the height to which the water rises in the cylindrical vessel.
16) A rectangular tank whose dimension are 30 cm, 20cm and 10cm is full of water. The water poured into a conical vessel of height 28cm. If the conical vessel is completely filled, find its base radius.
17) A conical tent is to accommodate 11 persons. Each person must have 4 m² of the space on the ground and 20 m² of air to breathe. Find the height of the cone.
18) A cone of maximum size is curved out of a cube of edge 14cm. Find the volume of the cone and of the remaining material.
19) A solid cone of height 8cm and base radius 6cm is a melted and recast into identical cones, each of height 2cm and diameter 1cm. Find the number of cone formed.
20) A hollow cylindrical pipe 50cm long, whose external diameter is 7cm and the internal diameter is 5cm, is melted and recast into a right circular cone, whose base radius is 10cm. Calculate the height of the cone.
21) A tent of height 8.25m is in the form of a right circular cylinder with diameter of base 30m and height 5.5m, surmounted by a right circular cone of the same base. Find the cost of the Canvas of the tent at the rate of Rs44 per m².
22) The interior of a building is in the form of a cylinder of the base radius 12m and height 3.5m surmounted by a cone of equal base and slant height 13m. Find the internal curved surface area and the capacity of the building.
23) From a cubical solid of metal 42cm x 30cm x 20 cm, a conical cavity of base radius 14cm and height 20cm is drilled out. Find :
a) the surface area of the remaining solid.
b) the volume of the remaining cavity.
c) the weight of the conical cavity if the metal weighs 7gm per cm³.
24) A right triangle with side 3cm and 4cm is revolved around its hypotenuse. Find the volume and surface area of the double cone thus generated .
25) What quantity of Canvas 1.25m wide will be required to make a conical tent whose radius is 21m and slant height 30 m ?
1) If 3/4, a, 2 are in AP then a=?
a) 3/8 b) 5/8 c) 7/8 d) 11/8
2) What is the next term of the AP √8, √18, √32,...?
a) √40 b) √48 c) √50 d) √54
3) What is the next term of the AP √2, √8, √18,.....?
a) √24 b) √28 c) √32 d) √32
4) Which term of the AP 5, 8, 11, 14,..... is 323 ?
a) 108th b) 107th c) 106th d) 54th
5) Which term of the AP 92, 88, 84,.... is 0?
a) 24th b) 27th c) 23rd d) 28rh
6) Which term of the AP 27, 24, 21, 18, ..... is -81 ?
a) 39th b) 38th c) 37th d) 29th
7) Which term of the AP 40, 35, 30,.... is the first negative term?
a) 9th b) 10th c) 12th d) 14th
8) Which term of the AP 5/6, 1, 7/6,.....is 14/3 ?
a) 26th b) 25th c) 24th d) 19tth
9) The 5th and 13th terms of an AP are 5 and- 3 respectively. The 24th term of this AP is
a) - 6 b) - 8 c) - 11 d) - 40
10) The 2nd, 31st and the last term of an AP are 31/4, 1/2 and -13/2 respectively . How many terms are there in this AP?
a) 53 b) 56 c) 59 d) 62
11) The 10th term from the end of the AP 7, 10, 13,.... 184 is
a) 151 b) 154 c) 160 d) 157
12) The 12th term from the end of the AP 17, 14, 11,.... - 61 is
a) -31 b) -28 c) -34 d) -37
13) If 4, x₁ , x₂, x₃, 28 are in AP then x₃ =?
a) 24 b) 22 c) 20 d) cannot be determined
14) The sides of a right triangle are in AP. The ratio of their length is
a) 1: 2: 3 b) 2:3:4 c) 3:4:5 d) 5:8:3
15) How many 2-digit numbers are there which are divisible by 6 ?
a) 14 b) 15 c) 16 d) 17
16) How many numbers are there between 102 and 750 which are divisible by 8 ?
a) 75 b) 78 c) 81 d) 84
17) If the nth term of a progression be a linear expansion in n then the given progression is
a) an AP b) a GP c) an HP d) none
18) In a given AP if pth term is q and the qth term is p then its nth term is
a) (p+ q+ n) b) (p+ q- n) c) (p- q+ n) d) (p- q- n)
19) In a given AP if mth term is 1/n and nth term is 1/m then its (mn)th term is
a) (1/m + 1/n) b) mn c) 1/mn d) 1
20) In an AP if m times the mth term is equal to n times the nth term then its (m + n)th term is
a) -(m+ n) b) -1 c) 1 d) 0
21) ( 5 + 9 + 13 + 17 +.....up to 23 terms)=?
a) 1123 b) 1127 c) 1131 d) 1135
22) (0.7 + 0.71 + 0.72 + .... up to 100 terms)=?
a) 117.5 b) 118.5 c) 119.5 d) 121.5
23) (25 +28 +31 + ....+100)=?
a) 1545 b) 1585 c) 1625 d) 1525
24) (1 + 3 + 5 + 7 + ....+999)=?
a) 251001 b) 249500 c) 249496 d) 250000
25) (101 + 99 + 97 +....+ 47)=?
a) 2076 b) 2072 c) 2177 d) 2173
26) If (1 + 6 + 11+....+x)= 148 then x=?
a) 8 b) 48 c) 36 d) 54
27) If (26 + 21 + 16+....x)=11 then x=?
a) - 12 b) - 18 c) - 24 d) - 30
28) How many times of the AP -5, -9/2, -4,...., will give the sum 0 ?
a) 21 b) 18 c) 23 d) 16
29) The 3rd term of an AP is 1 and its 6th term is -11. The sum of 32 terms of this AP is
a) 1696 b) -1696 c) 848 d) -848
30) The sum of first 7 terms of an AP is 10 and the sum of the next 7 terms is 17. What is the 3rd term of the AP ?
a) 9/7 b) 10/7 c) 12/7 d) 2
31) The sum of the first 80 natural number is
a) 3236 b) 3240 c) 3248 d) 3250
32) The sum of all even natural numbers between 300 and 400 is
a) 17350 b) 17250 c) 17150 d) 17400
33) The sum of all odd numbers between 100 and 200 is
a) 7500 b) 7450 c) 7560 d) 7600
34) The sum of all positive integral multiples of 3 less than 100 is
a) 1686 b) 1683 c) 1680 d) 1677
35) How many terms of the AP 6, 12, 18, 24,....must be taken to make the sum 816 ?
a) 16 b) 18 c) 14 d) 22
36) The sum of all 3-digit numbers divisible by 5 is
a) 97650 b) 98550 c) 95850 d) 96950
37) The sum of n terms of an AP is (3n²+ 2n). Its common difference is
a) 5 b) - 5 c) 6 d) - 6
38) The sum of n terms of an AP is (3n²+ 5n). Which of its terms is 164 ?
a) 28th b) 27th c) 26th d) 29th
39) If the sum of first m terms of an AP is the same as the sum of its first n terms then the sum of its first (m + n) terms is
a) 0 b) 1 c) 2(m + n) d) none
40) If the mth term of an AP is (1/n) and the nth term is (1/m) then the sum of its mn terms is
a) (mn+1)/2 b) 2(m+ n) c) -(m + n) d) none
41) If the sum of first m terms is n and the sum of first n terms is m, then the sum of first (m + n) terms is
a) 0 b) (m + n) c) -(m + n) d) -2(m + n)
42) if the sum of n terms of progression be quadratic expression in n then it is
a) an AP b) a GP c) an HP d) none
43) The sum of n terms of an AP is given by Sₙ= (3n²+ 4n). Its rth term is
a) (3r+4) b) (4r +3) c) (5r+2) d) (6r+1)
44) If S₁, S₂, S₃ be the sum of n, 2n and 3n terms of an AP respectively and (S₂ - S₁)= kS₃ then k=?
a) 1/2 b) 1/3 c) 2 d) 3
45) The sum of all 2-digit number is
a) 4750 b) 4895 c) 4905 d) 4850
46) The second and 7th terms of an AP are 2 and 22 respectively. The sum of its first 35 terms is
a) 2160 b) 2240 c) 2310 d) 2470
47) The first and fifth term of an AP are -14 and 2 respectively and the sum of its n terms is 40. Then, n =?
a) 8 b) 10 c) 12 d) 13
48) If (aⁿ⁻¹ + bⁿ⁺¹)/(aⁿ+ bⁿ) is the arithmetic mean between unequal numbers a and b then n=?
a) 0 b) 1 c) 2 d) 4
49)
50)
51)
52)
53) Three numbers are in AP whose sum is 24 and whose product is 440. The largest of these numbers is
a) 13 b) 11 c) 9 d) 12
54)
55) If (2+ 5 + 7 +.... to n terms)/(5 + 8 + 11+.. to 10 terms)= 7 then n=?
a) 35 b) 34 c) 32 d) 30
56) How many numbers lie between 10 and 300, which when divided by 4 leave a remainder 3 ?
a) 71 b) 72 c) 73 d) 74
57) Two APs have the same common difference and their first terms are - 1 and -8 respectively. The difference between their 4th terms is
a) 4 b) 5 c) 6 d) 7
58) If (k -1), (2k +1), (6k +3) are in GP then k=?
a) 7 b) 4 c) -2 d) 0
59) For what values of x are the numbers -2/7, x, -7/2 in GP?
a) -1 and 1 b) -1 and 2 c) -2 and 1 d) -2 and 2
60) The 17th term of the GP 2, √8, 4, √32,.... is
a) 256 b) 512 c) 128√2 d) 256√2
61) The nth term of the GP 12, 4, 4/3, 4/9,... is
a) 4/3ⁿ⁻¹ b) 4/3ⁿ⁻² c) 4/3ⁿ⁻³ d) none
62) Which term of the GP 5, 10, 20, 40, .... is 5120 ?
a) 9th b) 10th c) 11th d) 12th
63) Which term of the GP √3, 3, 3√3,.... 729?
a) 11th b) 12th c) 10th d) 13th
64) if the fourth and 9th term of a GP are 54 and 13122 respectively then its 6th term is
a) 243 b) 1458 c) 486 d) 729
65) The 4th and 7th terms of a GP are 1/18 and -1/486 respectively . Its first term is
a) 2/3 b) -2/3 c) 3/2 d) -3/2
66) The 8th term from the end of the GP 3, 6, 12, 24,....12288 is
a) 96 b) 192 c) 48 d) 288
67) The 6th term from the end of the GP 8, 4, 2,...., 1/1024 is
a) 1/64 b) 1/32 c) 1/128 d) 1/16
68)
69) if a, x, b are in GP then
a) x= ab b) x²= ab c) x= ab/2 d) x= (a+ b)/2
70) The arithmetic mean of two numbers is 34 and their geometric mean is 16. The numbers are
a) 64 and 4 b) 52 and 16 c) 56 and 12 d) 60 and 8
71) if 1/3, a, b, 9 are in GP then b=?
a) 1 b) 3 c) 6 d) cannot be determined
72) if the nth term of a GP is 2ⁿ, the sum of its six times is
a) 124 b) 126 c) 190 d) 254
73) (1+ √3+ 3 +3√3+....up to 10 terms)=?
a) 81(√3+1) b) 100(√3+1) c) 121(√3+1) d) none
74) (0.15+ 0.015+ 0.0015+....to 8 terms =?
a) (1/6)(1- 1/10⁷)
b) (1/6)(1+ 1/10⁸)
c) (1/6)(1- 1/10⁸)
d) (1/6)(1+ 1/10⁷)
75) (1- 1/2 + 1/4 - 1/8+..... to 9 terms )=?
a) 151/196 b) 161/225 c) 171/256 d) 181/256
76) (3 + 6 + 12 + ...+1536)=?
a) 1023 b) 2046 c) 3069 d) 4092
77) (2+6+18+54+....+4374)=?
a) 6450 b) 6560 c) 6670 d) 6380
78) In a GP it is given that a= 3, Tₙ = 96 and Sₙ = 189. The value of n is
a) 7 b) 8 c) 6 d) 5
79) How many terms of the GP 2, 6, 18....will make the sum 728 ?
a) 6 b) 9 c) 8 d) 7
80) How many terms of the GP 2/9- 1/3 +1/2 - ....must be taken to make the sum 55/72 ?
a) 6 b) 5 c) 7 d) 8
81) if the sum of n terms of a GP is (2ⁿ -1) then its common ratio is
a) 2 b) 3 c) 1/2 d) -1/2
82) In a GP, the ratio between the sum of first 3 terms and the sum of first 6 terms is 125 :152. The common ratio is
a) 1/2 b) 2/3 c) 3/5 d) 5/6
83) If the nth term of the GP 3, √3,1,....is 1/243 then n=?
a) 12 b) 13 c) 14 d) 15
84) For any two positive numbers , we have
a) AM≤GM b) AM≥ GM c) AM= 3GM/4 d) none
85) The AM between two positive numbers a and b (a> b) is twice their GM. then a:b=?
a) (3+√2):(3-√2) b) (2+√3):(2-√3) c) 2:3 d) none
86) GM between 27 and 243 is
a) 135 b) 3√3 c) 81 d) 40.5
87) GM between 0.15 and 0.0015 is
a) 1.5 b) 0.015 c) 0.15 d) none
24/11/24
R- 2
1) From In each of the following figures,if O is the centre of the circle, find the value of x and y. 50,75,80,128,48,50,40,115 and 65
a) ACD. 115
b) CAD. 40
a) SPQ. 118
b) PQR. 118
c) QRS. 62
4) in the figure,O is the centre and PQ is the diameter of the circle. If Angle PQR= 70 and angle RPS = 30, calculate the angle
a) QPR. 20
b) PRS. 40
5) in the figure,0 is the centre of the circle and AB is a diameter. If AB|| DC and angle BAC= 20, find the value of p, q, r and s. 40,100,50,110
7) In the figure,ABCD is a cyclic quadrilateral and DF || BC. if Angle EDF=15 and angle BAD= 80, find angle ABC. 115
9) In the figure,O is the centre of the circle and PS is a diameter. If Angle QPO= 35, find the angle
a) SOQ. 70
b) QRS. 145
10) In the figure,O is the centre of the circle. If Angle AOB= 140 and angle OAC = 50, find the angle
a) ABC. 40
b) BCO. 60
c) OAB. 20
d) BCA. 110
11) In the figure,AC is the diameter of the circle. If Angle DAB= 120 and angle ACB= 40 calculate the angle
a) ADB. 40
b) ABD. 20
12) In the figure,two circles Intersect at A and B. tohe centre of one circle lies on the circumference of other. If Angle AOB = 84, find the value of x. 69
a) QRS. 75
b) PSR. 75
c) PQR. 105
14) In the figure, ABCD is a cyclic quadrilateral, if Angle BCF = 48 and x= 2y, find the numerical value of x and y. 50,28
15) in the figure,AB is the diameter of the circle. If Angle APB= 120 and angle CBP= 25, find angle ADB. 95
16) In the figure,AB and CD pass through the centre O of the circle if Angle EBO = 40 and AOC= 75, find the value of x and y. 50,25
17) In the figure,O is the centre of the circle and a pentagon ABCDE is inscribed in it. If AB= BC= CD and angle ABC= 130, find the angle
a) AEB. 25
b) AED. 75
c) COD. 50
18) In the figure,P and Q are the centres of two circles intersecting at B and C . ACD is a straight line. Calculate the numerical value of x. 130
19) In the figure,O is the centre of the circle. If Angle AOE= 150 and angle DAO= 51, calculate the magnitude of angle
a) CEB. 51
b) CBE. 105
20) In the figure,length of Arc AB and arc BC are in the ratio 3:2. If Angle AOB= 96, Find the angle
a) BAC. 32
b) ADB. 132
21) ∆ PQR is inscribed in a circle with centre O. If Angle POQ = 140 and angle QOR= 116, find angle PQR. 52
22) ABCD is a cyclic quadrilateral in which the circle through A, B and C has D as its Centre. AB is produced to any point E. if Angle ADC= 136, find angle CBE. 68
23) Prove that every cyclic parallelogram is a rectangle.
24) PQRS is a cyclic quadrilateral in which angle QPR= angle RPS angle QRP= angle SRP. Show that PR is a diameter of the circle.
25) In the figure,chords AB and CD of a circle are produced to meet at O. Prove that ∆ OBD and ∆ OAC are similar.
26) Two circles with centres O and O' intersect at points A and B. AC and AD are their diameters respectively. prove that the points C, B and D are collinear .
27) PQ is a chord of a circle with centre O, R is any point on the minor arc PQ. Prove that angle POQ+ 2 angle PRQ= 360.
28) pr4ove that the quadrilateral formed by angle bisectors of a cyclic quadrilateral ABCD is also cyclic.
29) AB and BC are two equal chords of a circle. Prove that bisectors of angle ABC passes through the centre.
30) In the figure,AB and CD are two chords of the circle, with centre O which Intersect at right angles. Show that angle OAD= angle BDC.
31) Prove that the rhombus inscribed in a circle is a square.
32) ABCD is a cyclic quadrilateral in which AB and DC on being produced, meet at P such that PA= PD. Prove that AD is parallel to BC.
33) Prove that an isosceles trapezium is always cyclic .
34) In the figure,O is the centre of the circle. Chord AB is parallel to chord CD and CB is a diameter. Prove that Arc AC= Arc BD.
35) C is a point on the minor arc AB of a circle with Centre O.Given angle ACB= x°, angle AOB= y°, Express y in terms of x. calculate x if ACBO is a parallelogram . 2(180-x), 120
36) PQRS is a cyclic run which PQ= RS. Prove that angle PQR= angle SRQ.
37) X is a point on a circular with Centre O . If X is equidistant from the two radii OP, OQ, then prove that Arc PX= Arc QX.
38) in the figure,∆ ABC is an isosceles triangle inscribed in a circle with Centre O . If AB= AC, prove that AP bisects angle BPC.
39) if a pair of opposite side of a cyclic quadrilateral are equal, prove that its diagonals are equal.
40) in the figure,ABC is an isosceles triangle with AB= AC. A circle is drawn on AB as diameter. Prove that the circle bisects.
22/11/24
1) Manish bought a fan from a shop on the marked price of Rs2100. If the rate of GST is 12%, find:
a) the tax (GST) that Manish has to pay.
b) the total amount Manish has to pay for the fan.
2) In an intrastate transaction, goods worth Rs 8100 are bought . If GST rate is 18%, find :
a) IGST.
b) CGST.
c) SGST .
d) the amount of the bill.
3) in an intrastate transaction goods worth Rs46000 are bought at 10% discount. If the rate of GST 12%, then find
a) IGST.
b) Amount of the bill.
4) Ritika lives in New Delhi. She buys a washing machine of marked price Rs26000 and an LED TV of marked price Rs42000 from a showroom in New Delhi. The dealer offers a discount of 10% on washing machine and a discount of 20% on LED TV. If the rate of GST is 10%, find
a) IGST.
b) CGST.
c) SGST.
d) the amount paid by Ritika for these two items.
5) In intrastate transaction, goods worth Rs16000 are bought , if the rate of GST is 5%. Find the amount of the bill.
6)A customer buys a suitcase from a dealer at a discount of 8% on the marked price of Rs5000. If the rate of GST is 12%, calculate:
a) the tax(GST ) that the customer has to pay for the purchase.
b) the total amount that the customer has to pay for the suitcase.
7) A dealer in Jaipur sells a monitor to a customer in Jaipur at Rs7200. If the rate of GST is 18%, find :
a) IGST
b) CGST
c) SGST
d) the amount paid by the customer for the monitor.
8) In an interstate transaction, goods worth Rs 42000 are bought at 25% discount. If the rate of GST 12%, find
a) IGST
b) the amount of the bill.
9) An AC machine in Mumbai charges repairing cost from three different customers in Mumbai as below:
Customers I II III
Repairing cost(inRs) 3000 4000 2500
Discount 10% 5% 8%
If the rate of GST is 18%, find
a) IGST
b) CGST
c) SGST
d) total amount of the bill paid by customer.
10) A wholesaler in Agra (UP) bought goods from a dealer in Ranchi (Jharkhand). He bought :
i) 50 rings, Marked Rs 4000 each, at a discount of 40%.
ii) 40 necklaces, marked Rs2400 each, at a discount of 25%.
If the rate of GST on both items is 18%, how much will the wholesaler at Agra pay to dealer in Ranchi ?
ANGLES PROPERTIES OF A CIRCLE
R-1
20/11/24
ANGLES PROPERTIES OF A CIRCLE
R-1
1) In the figure, AC is the diameter of the circle, with centre O. CD and BE are parallel. If Angle AOB= 80 and angle ACE= 10. Calculate
a) angle BEC. 50
b) angle BCD. 100
c) angle CED. 30
2) In the given figure,AB is a diameter of the circle with centre O. ADE and CBE are straight lines . if Angle BED= 25 and angle BAD= 35, find
a) angle BCD. 35
b) angle CBD . 115
c) angle BDC. 30
3) in the figure,AC is the diameter of the circle with Centre O. Chord BD is perpendicular to AC. Write down the angles p, q, r in terms of x. 90- x/2, x/2, 90- x/2
4) in the figure,the centre O of the smaller circle lies on the circumference of the bigger circle. If Angle APB=75 and angle BCD= 40, find the angle
a) AOB. 150
b) ACB. 30
c) ABD. 110
d) ADB. 30
a) its other two sides are equal.
b) its diagonals are equal.
6) D and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD= AE.Show that B, C, E and D are concyclic.
a) APB. 80
b) AOB. 120
a) DBA. 30
b) BAD. 60
10) In the figure,AE is the diameter of a circle. Write down the numerical value of angle ABC+ angle CDE. Give reason for your answer. 270
a) DAB. 50
b) ADB. 40
12) In the figure,A, D, B, C are 4 points on the circumference of a circle with centre O. Arc AB= 2 Arc BC and angle AOB=108. calculate in degrees
a) ACB. 54
b) CAB. 27
c) ADB. 126
a) ABC. 76
b) BEC. 28
14) in the figure,ABCD is a cyclic quadrilateral, angle ADC= 80 and angle ACD= 52 p. Find the values of angle
a) CBD. 48
b) ABC. 100
15) Prove that the angle which an Arc of a circle subtends at the centre is double the angle which it subts at an any point in the remaining part of the circumference
17/11/24
SIMILARITY (AS A SIZE TRANSFORMATION)
1) Figures which have exactly the same shape , but not necessary the same___, are said to be similar.
a) angle b) side c) size d) volume
2) all regular polygons having the same number of ___are similar.
a) sides b) medians c) diagonals d) altitudes
3) Two circles are always :
a) congruent b) similar c) enarged d) concentric
4) in size transformation, the given figure is called an object and the resulting figure is called its:
a) pre- image b) image c) post image d) enlarge object
5) let K be the scale factor of a given size transformation . Then K< 1 as the transformation is a:
a) enlargement b) identify transformation c) transformation d) preserved
6) Each side of the resulting figure= ____ times the corresponding side of the given figure.
a) k² b) k c) k³ d) 2k
7) The transformation is an____ if k= 1 where k is the scale factor of a given size transformation.
a) identify transformation b) reduction c) enlargement d) none
8) in case of solids, we have volume of the resulting figure = ____x (volume of the given figure), where k is the scale factor.
a) k b) k² c) k³ d) 3k
9) if scale factor, k= 1/p, then area of the model= ____ x (area of the actual figure).
a) k² b) k c) k² d) 1/p
10) Let the map of a plane figure be drawn to the scale 1: p. Then scale factor k= ____, length in the map= k x (actual length (.
a) p/1 b) 1/p c) 1/k d) k
SHORT ANSWER TYPE OF QUESTIONS
1) ∆ ABC with sides AB= 12cm, BC= 8cm and AC= 14cm is enlarged to ∆A'B'C' such that the smallest side of ∆ A'B'C'= 12cm. Find the scale factor and use it to find the length of the other sides of the image A'B'C'.
2) ∆ ABC is reduced by scale factor 0.72. if the area of ∆ ABC is 62.5cm², find the area of the image.
3) A rectangle hving an area of 60cm² is transferred under enlargement about a point in space. If the area of its image is 135cm², find the scale factor of the enlargement.
4) In the map of a rectangular plot of land the length= 2.5 cm and breadth=1.4cm. if the scale 1: 1000, then find the area of the plot in m².
5) The surface area of a solid is 5m², while surface area of its model is 20 cm². Find
a) the scale factor
b) the volume of the solid if the volume of the model is 100cm³.
6) Two bottles of sauce of circular cross-section are completely similar in every respect. One is 24cm high and the other is 32 cm high.
a) Calculate the external diameter of the smaller bottle, given that the corresponding diameter for the other bottle is 8cm.
b) The smaller bottle can hold it 270cm³ of sauce. How much souce can the bigger bottle hold?
7) The model of a building is constructed with scale factor 1:30.
a) If the height of the model is 80cm, find the actual height of the building in metre.
b) If the actual volume of the tank on the tap of the building is 27m³, find the volume of the tank on the top of the model .
8) Two similar cylindrical tins have base radii of 6cm and 8cm respectively. Find the capacity of the smaller tin, if the capacity of the largest tin is 256 cm³.
LONG ANSWER TYPE QUESTIONS
1) The model of a ship is made to a scale 1:200.
a) The length of the model is 4m. Calculate the length of a ship.
b) The area of the deck of the ship is 160000m². Find the area of the deck of the model.
c) The volume of the model is 200 litres . Calculate the volume of the ship in m².
2) On a map drawn to a scale of 1:250000 a triangular plot of land has the following measurements: AB= 3cm, BC = 4cm, angle ABC= 90°
Calculate:
a) the actual length of AB in km
b) the area of the plot in km².
3) On a map drawn to a scale of 1:25000, a rectangular plot of land ABCD has the following measurements .
a) The diagonal distance of the plot in km.
b) The area of the plot in km².
4) The scale of a model ship is 1:300.
a) if the length of the model is 250cm, find the actual length in m.
b) if the desk area of the model is 1 m², find the deck area of the ship and the cost of painting it at Rs10 per m².
c) If the volume of the ship is 108000000 m³, find the volume of the model.
5) The dimension of the model of the multistoreyed building are 1m x 60 cm x 1.25m. if the model is drawn to a scale 1:60, find the actual dimensions of the model in metres . Also find
a) the floor area of a room of the building, whose area in the model 250 cm².
b) the volume of the room in the model whose actual volume is 648 m³.
SIMILARITY OF TRIANGLES
1) Figures which have exactly the same shape , but not necessarily the same____, are said to be similar.
a) angle b) side c) size d) volume
2) All regular polygon having the same number of____ are similar.
a) sides b) medians c) diagonals d) altitudes
3) Two circles are always:
a) congruent b) similar c) enlarged d) concentric
4) In size transformation, the given figure is called an object and the resulting figure is called its:
a) pre-image b) image c) post-image d) enlarge object
5) let k be the scale factor of a given size transformation. Then k < 1 as the transformation is a:
a) enlargement b) identify transformation c) reduction d) preserved
6) Each side of the resulting figure= ____ times the corresponding side of the given figure.
a) k² b) k c) k³ d) 2k
7) The transformation is an____, if k=1 where k is the scale factor of a given size transformation.
a) identify transformation b) reduction c) enlargement d) none
8) In case of solids, we are volume of the resulting figure = ____ × (volume of the given figure), where k is the scale factor.
a) k b) k² c) k³ d) 3k
9) If a scale factor, k= 1/p, then area of the model= ____ × (area of the action figure).
a) k² b) k c) k³ d) 1/p
10) Let the map of a plane figure be drawn to the scale 1: p. Then scale factor k= ___, length in the map = k × (actual length).
a) p/1 b) 1/p c) 1/k d) k
13/11/24
RATIO AND PROPORTION
1) If x², 4 and 9 are in continued proportion, then the value of x is:
a) 2/3 b) 4/3 c) 3/4 d) 16/9
2) if a: b = 5 : 3, then (5a + 8b): (6 a - 7b) is equals to:
a) 40 : 9 b) 9 : 49 c) 49 : 9 d) 25: 9
3) The fourth proportional to 7, 13 and 35 is:
a) 65 b) 62 c) 52 d) 50
4) The third proportional to 9 and 15 is:
a) 10 b) 15 c) 18 d) 25
5) if (7m + 2n)/(7m - 2n)= 5/3 then m: n is:
a) 7 : 8 b) 2:7 c) 8 : 7 d) 1:8
6) The mean proportion between 28 and 63 is:
a) 42 b) 45 c) 36 d) 32
7) if fourth proportional to 3,12, 15 is:
a) 40 b) 45 c) 60 d) 62
8) If x : y= 2:3 then (3x +2y)/(2x + 5y) is:
a) 12/19 b) 19/12 c) 12/13 d) 19/21
9) The mean proportion between x-y and x³ - x²y is :
a) x(x + y) b) x²(x - y) c) x²(x + y) d) x(x - y)
10) If a :b = 2: 3 and b: c= 4:5, then a: c is
a) 12 :15 b) 15:7 c) 15:8 d) 8:15
11) If a/b = c/d, then (a+ c)/(b+ d) is equal to
a) a/b b) c/d c) both a and b d) neither a nor b
12) The fourth proportional to 3, 6 and 4.5 is
a) 10 b) 9 c) 8.5 d) 6
13) The third proportional to x - y and x²- y² is
a) (x + y)(x²- y²) b) (x - y)(x² +y²)
c) (x² + y²)(x²- y²) d) (x + y)(x- y)
14) if a/b : c/d, then each ratio is equals to :
a) a+ b : c+ d b) a+ c : b + d c) a+ d: b + c d) a- b: c - d
15) the mean proportion between a²b and 1/b is
a) a b) a² c) ab d) √(ab)
16) If 2x = 3y and 4y= 5z, then 8x/z is equals to
a) 5 b) 15 c) 10 d) 8
17) Two numbers are in the ratio 1 :4. If the mean proportion between them is 28 and third proportional to them is 224, then the smaller number is
a) 12 b) 14 c) 16 d) 21
18) if three quantities a, b, c are continued proportion, then the mean proportion between
a) a and c is b b) b and c is a c) c and a is b d) all the above are true
19) x, y, z are in continue proportion, then x/z is equals to
a) y²/z² b) y²/x² c) x²y² d) x/y²
20) If (4a + 9b)/(4c + 9d) = (4a - 9b)/(4c - 9d), then a: b=
a) c: d b) d: c c) c: d+ c d) d: c - d
SHORT QUESTIONS
1) If (3a + 2b) : (5a + 3b)= 18: 29, find a, b.
2) What least number must be added to each of the numbers 2, 5, 18 and 33, so that the resulting numbers are proportional .
3) If b is the mean proportiona between a and c, show that b(a+ c) is the mean proportion between (a²+ b²) and (b²+ c²).
4) If a: b = c : d, then prove that (a+ b): (c + d)= √(a²+ b²): √(c²+ d²).
5) If x/(b - c) = y/(c - a)= z/(a - b), then show that ax+ by + cz =0.
6) If a, b, c, d are in continued proportion, prove that (b + c)(b + d)= (c + a)(c + d).
7) it a/b = c/d, then, show that (3a - 5b)/(3a + 5b)= (3c - 5d)/(3c + 5d).
LONG ANSWER
1) If b is the mean proportion between a and c, show (a²+ b²+ c²)/(a⁻² + b⁻² + c⁻²) = b⁴.
2) if a, b, c are in continued proportion, show that (2a²+ 7b²- 5ab)/(2b²+ 7c²- 5bc)= a/c.
3) If a, b, c, d are in continued proportion, show that
√(ab) + √(bc) - √(CD)= √(a+ b - c)(b + c - d).
4) If a: b= c : d, show that (a²+ c²+ ac): (a²+ c²- ac)= (b²+ d²+ bd):(b²+ d²- bd)
5) If ax = by = cz, then show that x²/yz + y²/zx + z²/xy = bc/a²+ ca/b²+ ab/c².
6) If x= {√(a+ 3b) +√(a - 3b)}/{√(a+ 3b)- √(a - 3b)}, show that 3bx²- 2ax + 3b = 0
7) If p= 4xy/(x + y), show that (p+ 2x)/(p- 2x) + (p+ 2y)/(p - 2y)= 2.
8) If If {√(a+ 15) +√(a - 6)}/{√(a+ 15)- √(a - 6)}= 7/3, find the value of a.
9) If 11 = {√(6x)+√(3x +7)}/{√(6x)- √(3x+7)}, then find x
10/11/24
Section formula
1) In what ratio is the line joining (2, -3) and (5,6) divided by x-axis. 1:2
2) In what ratio is the line joining (2, -4) and (-3, 6) divided by x-axis. 2:3
3) Calculate the Co-ordinates of the point P which divides the line joining A(-1,3) and B(5,9) in the ratio 1:2. (1,5)
4) The line joining the points A(-3, -10) and B(-2,6) is divided by the point P such that PB/AB = 1/5. Find the coordinate of P. (-11/5, 14/5)
5) P is a point on the line joining A(4,3) and B(-2,6) such that 5AP/2BP. Find the coordinates of P. (16/7,27/7)
6) In what ratio does the point P(3,3) divide the join of A (1,4) and B(7,1)? 1:2
7) In what ratio does the point (1,a) divide the join of (-1, 4) and (4,-1)? Also find the value of a. 2:3, 2
8) In what ratio does the point (a,6) divide the join of (-4,3) and (2,8)? Also find the value of a. 3:2, -2/5
9) In what ratio is the join of (4,3) and (2, -6) divided by x-axt. Also find the Co-ordinates of the point intersection. 1:2, (10/3,0)
10) Find the ratio in which the join of (-4,7) and (3,0) divided by y-axis. Also find the coordinates of the point of intersection. 4:3, (0,3)
11) Points A, B, C and D divide the line segment joining the point (5, -10) and origin in five equal parts. Find the coordinates of A, B , C and D. (4,-8), (3,-6),(2,-4),(1,-2)
12) Find the Co-ordinates of the points of trisection of the line joining the points (-3,0) and (6,6). (0,2),(3,4)
13) Show that the line segment joining the point (-5,8) and (10,-4) is trisected by coordinate axes.
14) Show that A(3,-2) is a point of trisection of the line segment joining the point (2,1) and (5,-8).
Also, find the coordinates of other point of trisection . (4,-5)
15) Given , two fixed points A(0,10) and B(-30 ,0). Calculate the coordinates of a point P which lies in the AB such that:
a) 2AP 3PB.
b) 3AP = AB
c) 7PB = AB
16) Given two fixed points P(-3,4) and Q(5,-2). Calculate the coordinates of points A and B in PQ such that:
5PA= 3PQ and 3PB = 2PQ.
17) The line segment joining A(2,3) and B(6,5) is intersected by x-axis at point K. Write down the ordinate of K. Hence, find the ratio in which K divides AB.
18) The line segment joining the points M(5,7) and N(-3,2) is interesting by y-axis at point L. Write down the absicca of L. Hence, find the ratio in which L divides MN.
Also the Co-ordinates of L.
19) Calculate the coordinates of points which devide the join of (8, 6) and (2,.3) into 4 equal parts. (13/2,21/4),(5,9/2) and (7/2,15/4)
20) A(2,5), B(-1,2) and C(5,8) are the coordinates of the vertices of the triangle ABC. Points P and Q lie on AB and AC respectively, such that :
AP: PB = AQ : QC= 1:2.
a) calculate the Co-ordinates of P and Q. (1,4)
b) Show that PQ= (1/3)BC
21) A(-3,4) B(3,-1) and C(-2,4) are the vertices of a triangle ABC. Find the length of line segment AP, where point P lies in side BC, such that BP: PC = 2:3.
GOODS AND SERVICES TAX
Multiple Choice Questions
1) IGST is charged on:
a) interstate transaction b) intrastate transaction c) both a, b d) none
2) GST payable is equals to
a) ITC --output GST b) output GST + ITC c) output GST - ITC d) output GST
3) A dealer in Mumbai sold a washing machine to a consumer in Mumbai for Rs18000. If the rate of GST is 18% and GST, then SGST is:
a) Rs1620 b) Rs3240 c) nil d) none
4) In a transaction from Delhi to Lucknow, MRP = Rs10000, discount= 10%, GST= 28%. Here IGST is:
a) Rs2520 b) Rs5040 c) nil d) none
5) A refrigerator was sold for Rs15000 under intrastate transaction from station A to station B and the GST rate is 18%. CGST is:
a) Rs1450 b) Rs 1350 c) Rs1300 d) Rs2700
6) A dealer purchased goods worth Rs 15000 and sold them for Rs21000 within the state. If the rate of GST is 12%, then the net SGST paid by the dealer is:
a) Rs360 b) Rs720 c) Rs800 d) Rs850
7) A dealer in Delhi sold a water heater whose marked is Rs22000 to a customer in Delhi at discount of 25%. If the rate of GST 18%, then the SGST paid is:
a) Rs 1485 b) Rs2970 c) Rs1980 d) nil
8) Anushka bought 400g of almonds at Rs1200 per kg. If the rate of GST is 5%, the amount paid by Anushka is:
a) Rs504 b) Rs480 c) Rs1260 d) Rs630
9) A dealer in Agra sold an LED to a customer in Agra for Rs28000. If SGST is Rs2420, then the rate of GST is:
a) 12% b) 18% c) 9% d)28%
10) Mr. Sharma purchased goods worth Rs40000 from a dealer(within the same state ). If the rate of GST 18%, then CGST is:
a) Rs 3600 b) Rs7200 c) Rs8000 d) nil
11) The tax invoice of a mobile company in Delhi shows cost of services provided by it as Rs1200. If the rate of GST is 18%, then amount of the bill is:
a) Rs 1400 b) Rs1308 c) Rs 1416 d) Rs1500
12) A shopkeeper in Rampur sold an oven to a customer in Rampur for Rs26400. If the rate of GST is 28%, then IGST is:
a) Rs3696 b) Rs7392 c) Rs1848 d) nil
13) A dealer in Bhopal (MP) supplies goods worth Rs 30000 to a dealer in Delhi. The dealer in Delhi supplies the same goods to a customer in Delhi at a profit of Rs5000. If the rate of GST is 18%, then the net GST paid by the dealer in Delhi is:
a) Rs900 b) Rs2700 c) Rs5400 d) nil
14) A dealer in Patna (Bihar) supplies goods worth Rs 15000 to a dealer in Sonepat(Haryana). The dealer in Sonepat supplies the same goods to a dealer in Rohtak (Haryana) at a profit of Rs 3000. If the rate of GST is 18%, then the net GST paid by the dealer in Sonepat is:
a)Rs 540 b) Rs700 c) Rs720 d) nil
15) A retailer purchases an iron for Rs1500 from a dealer and sells it to a consumer at 10% profit. If the sales and intrastate , and the rate of GST is 12%, then the selling price of the iron including GST by the retailer is:
a)!Rs1550 b) Rs1848 c) Rs1950 d) Rs
16) A shopkeeper purchased a fan for Rs1500 from a dealer and sold it to a customer at 10% profit. If the sells are intrastate and the rate of GST is 12%, then the tax (under GST) received by the central government is :
a) Rs18 b) Rs99 c) Rs198 d) nil
17) Goods from Delhi are sold to Ranchi(Jharkhand) for Rs20000 and then from Ranchi to Cuttack (Odisha). If the rate of GST is 18%, and the profit made at Ranchi is Rs5000, then the net GST payable by the dealer in Ranchi is :
a) Rs1000 b) Rs900 c) Rs850 d) Rs875
18) A shopkeeper bought an article from a dealer at Rs1000. He sold it to the customer at Rs1200. If the rate of GST is 12%, then the amount paid by the customer to buy the item is:
a) Rs 1200 b) Rs1300 c) Rs1344 d) Rs1350
19) Three friends A, B and C live in Delhi. A sales medicine worth Rs50000 to B, B sells the same medicine to C at a profit of Rs 6000. If the rate of GST is 12%, then SGST paid by B is:
a) Rs300 b) Rs360 c) Rs400 d) Rs425
20) Mr Gupta wanted to book a semidelux room in a hotel for Rs750. Since semidelux room was not available, he booked a delux room for Rs1400. If GST for a room below Rs1000 is 18% and GST for a room above Rs1000 is 28%, then the extra GST paid by Mr Gupta for the delux room is:
a) Rs 257 b) Rs280 c) Rs300 d) Rs425
Answer:
1a 2c 3a 4a 5b 6a 7a 8a 9b 10a 11c 12 d 13 a 14a 15b 16b 17b 18c 19b 20a
Short Answer Type Questions:
1) Find the amount of bill for the following intrastate transaction of goods , if the GST rate is 28%.
items I II III
Marked price(Rs) 7000 14700 28200
discount% 20 10 10
2) A registered garment house in Ludhiana (Punjab) sold three lots of garments to a dealer in Bhatinda (Punjab) for Rs1000000; Rs600000 and Rs500000. It also charged Rs10000 on each lot of transportation charges . But on the occasion of Diwali , a discount of 1% was given on each lot . If the rate of GST is 5%, Calculate
a) IGST
b) CGST
c) SGST
3) Saurav went to watch a new movie in a multiplex. He wanted to buy a movie ticket for Rs80, but it was not available. So, he bought a ticket for Rs120. If the GST for a ticket below Rs100 is 18%, and GST for a ticket above Rs100 is 28%, how much extra GST and extra amount did saurav pay for the ticket?
4) A dealer in Rohtak (Haryana) bought a gold ring from a manufacturer in Gurgaon (Haryana) for Rs800000. He sold this ring to a dealer to Nainital (Uttarakhand) for Rs95000. If the rate of GST is 3% find
a) the new GST payable at Rohtak
b) Input tax credit (ITC) for dealer in Nainital.
5) A retailer in Jaipur( Rajasthan) buys goods from a dealer in Alwar (Rajasthan) at a discount 20%. The retailer sales it to a customer in Jaipur at the printed price. If the printed price of the goods is Rs16000 and the GST rate is 8%, calculate :
a) the prince paid by the customer for the goods.
b) the CGST and SGST payable by the retailer in Jaipur to the government.
Answer
1) Rs56588.80 2) 0, Rs52725, Rs52725 3) Rs19.20, Rs59.20 4) Rs450, Rs2850 5) Rs17280, 128, 129
LONG ANSWER TYPE QUESTIONS
1) An e-learning company in Delhi sets the marked price of an e-book as Rs75000. It sells the e-book to a dealer in Patna (Bihar) at discount of 30%. The dealer in Patna raises the marked price of the e-book by 30% and then sells it to a dealer in Ranchi (Jharkhand). if the rate of GST is 5%, find the GST paid by the dealer in Patna to the government.
2) A manufacturer in Noida (UP) sold a cartoon of hair oil to a dealer in Rajpur (Chhattisgarh) for Rs22000. The dealer in Raipur sold it to a consumer in Bastar (Chhattisgarh) at a profit of Rs5000. If the rate of GST is 18%, find:
a) the net IGST , CGST and SGST payable by the dealer in Raipur.
b) the cost price of the hair oil for the customer.
3) A dealer in Jodhpur (Rajasthan) supplied floor tiles worth Rs1700000 to a dealer in Delhi and another worth Rs300000 to a dealer in Jaipur (Rajasthan). The total value of his receipt of tiles in interstate transactions was Rs1500000. If the rate of GST is 18%, calculate the net IGST , CGST and SGST payable by the dealer in Jodhpur.
4) A shopkeeper sells an item for Rs2150. For a customer, he reduced the price of the item in such a way that the customer has to pay only Rs2124 including GST. If the rate of GST is 18%. Calculate the amount of reduction allowed by the shopkeeper .
5) A fruit juice company in Allahabad (UP) sold fruit juice worth Rs16000 to a dealer in Hapur(UP). The whole lot of juice was then supplied to a dealer in Rudrapur (Uttarakhand) for Rs17500. If the rate of GST is 12%. Find :
a) the net GST payable at Hapur.
b) input Tax credit (ITC) for the dealer in Rudrapur.
6) Radheshyam is a dealer of footwear in Moradabad (UP). He purchase footwear worth Rs200000. He sold 50% of thess footwear to a dealer in Agra (UP) for Rs130000 and the rest of the stock remains in his godown. If the rate of GST is 5%, find the excess credit of CGST and SGST to be carried forward.
7) The marked price of a video camera Recording is Rs80000. A dealer in Delhi buys it from a dealer in Mumbai (Maharashtra) at discount of 20% on the marked price . The dealer then sells it to a customer in Rohtak (Haryana) at a discount of 10% on the marked price. if the rate of GST is 18%, calculate the amount of tax payable by the dealer in Delhi to the government.
Answer
1) Rs2250 2) Rs0, Rs0, Rs900, Rs31860 3) Rs36000, Rs27000, Rs27000 4) Rs350 5) Rs180, Rs2100 6) Rs750, Rs750 7) Rs1440
HEIGHTS AND DISTANCES
1) State whether the following are true or false:
a) The angle of elevation of the sun when the length of the shadow of the pole is equal to its height 45°. T
b) If the ratio between the length of the shadow of a pole and its height is √3 : 1, then the elevation of the sun is 30°. T
c) If the ratio between the length of the shadow of a tower and its height is 1 : √3, then elevation of the sun is 50°. F
d) The numerical value of depression from the top of a tower of a point on the ground is same as elevation of the top from the point on the ground. T
2) The bpangles of the elevation of the top of a tower from two points distant 150m and 100m from the foot of the tower and in the same straight line with it, are complementary. Prove that the height of the tower is 50√6.
3) A plane is observed to be approaching the airport. It is at the distance of 12km from the point of observation and makes an angle of elevation of 50° there at. Find its height above the ground. 9.192km
4) Determine the height of a mountain if the elevation of its top at an unknown distance from the base is 25°10' and a distance 5km further off the mountain along the same line, the angle of elevation is 15°20'. 3.29 km
5) The shadow of a tower standing on a level ground is found to be 45 m longer, when the sun's altitude is 30° than when it was 60°. Find the height of the tower. 38.94m
6) A tower is 100√3m high. Find angle of elevation of its top from a point 100m away from its foot. 60°
7) The angle of elevation of a tower at a point is 45°. After going 40m towards the foot of the tower, the angle of elevation of the tower becomes 60°. Find the height of the tower . 94.64m
8) From the top of a hill, the angles of depression of two consecutive kilometre stones due east are found to be 30° and 45°. Find the height of the hill. 1366m
9) A person observed the angle of elevation of the top of a tower is 30°. He walked 50m towards the foot of the tower along level ground and found the angle of elevation of the top of the tower as 60°. Find the height of the tower. 43.3m
10) The string of a kite is 100m long and it makes an angle of 60° with the horizontal. Find the height of the kite, assuming that there is no slack in the string. 86.6m
11) A parachutist is descending vertically and makes angles of elevation of 45° and 60° at two observing points 100m apart from each other on the left side of himself. Find the maximum height from which he falls and the distance of the point where he falls on the ground from the first observation point. 236.6m, 136.6m
12) On the same side of a tower, two objects are located observed from the top of the tower, their angles of depression are 45° and 60°, if the height of the tower is 150m, find the distance between the objects. 63.4m
13) A surveyor noted that angle of elevation of a marker on the top of a hill was 15°24'. He walked 40m towards the foot of the hill along level ground and found the angle of elevation of the marker as 30°'30. How far from the surveyor's first position was the marker. ? 77.29
14) The shadow of a flagstaff is three times as long as the shadow of the flagstaff when the sun rays meet the ground at an angle of 60°. Find the angle between the sun rays and the ground at the time of longer shadow. 30°
15) The shadow of a vertical tower on level ground increases by 10m, when the altitude of the sun changes from angle of elevation of 45° to 30°. Find the height of the tower . 13.66m
16) The pilot of helicopter, at an altitude of 1200m, finds that the two ships are sailing towards it, in the same direction. The angles of depression of the ships as observed from the helicopter at 60° and 45° respectively. Find the distance between the two shops. 507.2m
17) The angle of elevation of an aeroplane from A on the ground is 45°. After 15 seconds flight , the angle of elevation changes to 30°. if the aeroplane is flying at a height of 3000m, find the speed of the plane. 146.6 m/sec
18) The angle of elevation of a jet fighter from a point P on the ground is 60°. After 15 seconds flight the angle of the elevation changes to 30°. if the jet is flying at a speed of 720 km per hour. Find the height at which Jet is flying . 2598 m
19) At a certain point, the angle of elevation of a tower is found to be such that its tangent is 5/3 on walking 32m directly, towards the tower, its angle of elevation has its tangent 5/2. Find the height of the tower. 160m
20) From the top of a cliff 100m high, the angles of depression of the top and bottom of a tower are observed to be 30° and 60° respectively. Find the height of the tower. 200/2m
21) From the top of a cliff 100m high, the angles of depression of the top and bottom of a tower are observed to be 32.6° and 45° respectively. Find the height of the tower. 336.05m
22) From the top of a building, 60m high, the angles of depression of the top and bottom of a vertical lamp-post are observed to be 30° and 60° respectively, Find
a) the horizontal distance between the building and the lamp post. 34.64
b) the difference between the heights of the building and the lamp post. 20m
23) The horizontal distance between two trees of different heights is 60m. The angle of depression of the top of the first tree when seen from the top of the second tree is 45°. if the height of the second tree is 80m, find the height of the first tree. 20m
24) The angle of depression of two ships on either side of a lighthouse as observed from the top of the lighthouse are 52° and 41°40' respectively. if the height of the lighthouse is 150m, find the distance between two ships . 285.795m
25) Two men are at opposite sides of a tower. They measure the angle of elevation of the top of the tower as 45° and 60° respectively. The height of the tower is 30m. Find the distance between the two men. 47.32m
26) Two points A and B are on opposite sides of a tower. The top of the tower makes angle of 30° and 45° at A and B respectively. if the height of tower is 40m, find the distance AB. 109.28
27) Two men are diemattrically opposite sides of a tower. They measure the angles of elevation of the top of the tower as 20° and 24° respectively . If the height of the tower is 40m, find the distance between the two men. 199.74
28) A fire in a building B is reported on telephone to two fire stations A and B, 10km apart from each other on a straight road A observes that fire is at an angle of 60° to the road and B observes that is an angle of 45° to the road. Which station should send its team and how much will this team have to travel ? The first team will have to travel 7.32 km
29) Two men on either side of the cliff 80 m high observes the angles of elevation of the top of the cliff to be 30° and 60° respectively. Find the distance between the two men. 184.8m
30) An aeroplane at an altitude of 200m observes the angles of depression of opposite points on the two banks of a river to be 45° and 60°. Find the width of the river. 315.4m
31) Two boats approach a light house in mid-sea from opposite directions , The angles of elevation of the top of the light-house from the two boats aree 30° and 45° respectively. if the distance between the two boats is 100m, find the height of the lighthouse. 36.6m
32) From the top of a lighthouse, the angles of depression of two ships on the opposite sides of it are observed to be α and β. if the height of the light-house be h meters and the line joining the ships passes through the foot of the light-house , show that the distance between the ships is h(tanα + tanβ)/(tanα tanβ).
33) A flagstaff stands on the top of a 5m high tower from a point on the ground. The angle of elevation of the top of the flagstaff is 60° and from the same point the angle of elevation of the top is 45°. Find the height of the flagstaff. 3.66m
34) A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is 30°and that of the flagstaff is 45°. Find the height of the tower. 9.562m
35) A vertical tower stands on horizontal plane and is surmounted by a vertical flagstaff . At a point on the plane 70m away from the tower, an observer notices that the angles of elevation of the top and bottom of the flagstaff are respectively 60° and 45°. Find the height of the flagstaff and that of the tower. 51.24m, 70m
36) A tree is broken by the wind. The top struck the ground at an angle of 30° and at a distance of 30m from the root. Find the whole height of the tree. 51.96m
37) The upper part of a tree broken over by the wind makes an angle of 30° with the ground and the horizontal distance from the root of the tree to the point where the top of the tree meets the ground is 20m. Find the height of the tree before it was broken. 34.64m
38) A tree 12m height is broken by the wind in such a way that is top touches the ground and makes an angle of 60° with the ground. At what height from the bottom the trees is broken by the wind ? 5.568m
39) There are two temples, one on each Bank of a river, just opposite to each other. One temple is 40 m high p. As observed from the top of this temple, the angle of depression of the top and foot of the other tower temple are 12°30' and 21°48' respectively. Find , in metres, the width of the river and height of the other temple approximately. 100m app. , 17.83 app
40) A tower in a city is 150m high and multistoreyed hotel at the city Centre is 20m high. The angle of elevation of the top of the tower at the top of the hotel is 5°. A building h metres high, is situated on the straight road connecting the tower with the city centre at a distance of 1.2 km from the tower. Find the value of h if the top of the hotel, the top of the building and the top of the tower are in a straight line. Also, find the distance of the tower form the city centre. (Tan 5°=0.0875, tan85°= 11.43). 287.7m, 44.998m
41) An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°. Find the speed of the aeroplane in km/hr. 415.68 km/hr
42) A man is standing on the deck of a ship, which is 8 m above water level. He observes the angle of the elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill form the ship and the height of the hill. 13.856m, 32m
43) In the given figure,ABCD is a rectangle in which segment AP and AQ are drawn as shown. Find the the length of (AP+ AQ). 180cm
44) At the foot of a mountain, the relation of its summit is 45°. After ascending 1 km toward the mountain of 30°, the elevation changes to 60°. Find the height of the mountain. 1.366 km
4/11/24
MEAN, MEDIAN AND MODE
R-1
1) Calculate the mean, the median and the mode of the following numbers : 3, 1, 5, 6, 3, 4, 5, 3, 7, 2.
2) The marks scored by 19 students in a test are given below :
31, 22, 36, 27, 25, 26, 33, 24, 37, 32, 29, 28, 36, 27, 35, 35, 32, 26, 28.
Find
a) median.
b) lower quartile.
c) upper quartile.
d) inter quartile.
3) From the following frequency distribution, calculate
a) median.
b) lower quartile.
c) upper quartile.
c) semi interquartile range.
Variate : 13 15 18 20 22 24 25
Frequency : 6 4 11 9 16 12 2
4) The marks obtained by 120 students in a mathematics test are given below:
Marks No of students
00-10 5
10-20 9
20-30 16
30-40 22
40-50 26
50-60 18
60-70 11
70-80 6
80-90 4
90-100 3
Draw an ogive for the given distribution on a graph paper. Use a suitable scale for your ogive .
Use your ogive estimate.
a) The median.
b) the lower-quartile.
c) The number of students who obtained more than 75% in the test.
d) the number of students who did not pass in a test if the pass percentage was 40.
R-2
1) The daily profits in rupees of 100 shops in a department store are distributed as follows:
Profit per shop(in Rs) No of shops
000-100 12
100-200 18
200-300 27
300-400 20
400-500 17
500-600 6
Draw a histogram of the above data on a graph paper and hence estimate the mode.
2) For the following set of the numbers, find the median: 10, 75, 3, 81, 17, 27, 4, 48, 12, 47, 9, 15 .
3) For the following frequency distribution, draw a histogram. Hence, calculate the mode
Class frequency
00- 05 2
05-10 7
10-15 18
15-20 10
20-25 8
25-30 5
4) The marks obtained by 200 students in an examination are given below:
Marks No of students
00-10 5
10-20 10
20-30 11
30-40 20
40-50 27
50-60 38
60-70 40
70-80 29
80-90 14
90-100 6
Using graph paper, draw an ogive for the above distribution. Use your ogive to estimate:
a) the median.
b) the lower-quartile.
c) the number of students who obtained more than 80% marks in the examination.
d) the number of students who did not pass, if the pass percentage was 35.
5) From the following table, find:
a) the average wave of a worker.
Give your answer correct to nearest paise.
b) the model class.
Wages No of workers
below 10 15
below 20 35
below 30 60
below 40 80
below 50 96
below 60 127
below 70 190
below 80 200
CENTRAL TENDENCY
R-1
1) Marks obtained by a set of students in an examination are given below:
Marks: 5 10 15 20 25 30
No of students: 6 4 6 12 x 4
Given that the mean mark of the set is 18, find the numerical value of x. 8
2) Using short - cut method, find the mean height from the following frequency distribution:
Height (in cm): 58 60 62 65 66 68
No of plants: 15 14 20 18 8 5 62.35
3) Using step deviation method, calculate the mean of the following data:
Marks. no of students
00-10 2
10-20 8
20-30 15
30-40 21
40-50 4
50-60 52
60-70 37
70-80 21
80-90 15
90-100 5 55.61
R-2
1) a) If 7 is the mean of 5, 3, 0.5, 4.5, b, 8.5, 9.5. find b. 18
b) If each observation is decreased by 1 unit, what would the new mean be ? 6
2) Find the mean of the following frequency distribution:
Class interval frequency
00-50 4
50-100 8
100-150 16
150-200 13
200-250 6
250-300 3 143
3) Given below are the weekly wages of 200 workers in a small factory:
Weekly wages (Rs) No of workers
80-100 20
100-120 30
120-140 20
140-160 40
160-180 90
Calculate the mean weekly wages of the workers. Rs145
4) The contents of 100 match boxes were checked to determine the number of matches they contained.
No of matches: 35 36 37 38 39 40 41
No of boxes: 6 10 18 25 21 12 8
a) Calculate, correct to one decimal places, the mean of matches per box. 38.19
b) Determine how many extra matches would have to be added to the total contents of the 100 boxes to bring the mean up to exactly 39 matches. 87
5) The histogram represent the marks obtained by some candidates in an examination. Using the data in the diagram. Calculate the mean mark. 23.33
6) Category A B C D E F G
Wages in Rs/day:50 60 70 80 90 100 110
No of workers: 2 4 8 12 10 6 8
a) Calculate the mean wage correct to the nearest rupee. Rs85
b) if the number of workers in each category was doubled, what would be the new mean wage ? Rs85
7) The following table gives daily wages of 50 workers of a factory.
Wages No of workers
25-30 2
3ó-35 3
35-40 5
40-45 7
45-50 21
50-55 10
55-60 2
Calculate the mean daily wages of the workers of the factory.
If the daily wages of all the workers are increased by Rs8, what will be the new mean daily wage of workers. Rs45.50, Rs53.50
R- 3
1) Find the arithmetic mean of the following:
a) First 10 natural numbers. 5.5
b) First five prime numbers. 5.6
c) First eight even natural numbers. 9
d) All the factors of 20. 7
2) Find the mean of the following marks of 20 students in a test:
76, 44, 45, 71, 87, 41, 83, 82, 32, 72, 32, 46, 75, 78, 17, 70, 74, 77, 84, 12. 59.9
3) Find the mean of the following set of the numbers:
a) 7, 12, 21, 9, 11, 14, 16, 19, 20, 25, 12, 2. 14
b) 5.8, 6.3, 7.1, 9.4, 4.9. 6.7
c) 2.6, 1.9, 7.2, 4.6, 5.8, 3.7. 4.3
4) if the mean of 6, 8, 5, 4, 7 and x is 7, find x. 12
5) The mean weight of 60 students of a class is 52.72 kg. If the mean weight of 25 of them 51kg, find the mean weight of the remaining students. 54kg
6) The mean weight of 70 observation was found to be 150. While checking, it was detected that one value 210 was wrongly copied as 140 while calculating the mean. Find the correct mean. 151
7) The marks obtained by 10 students in a test are: 6, 5, 8, 0, 7, 9, 3, 1, 5, 4.
a) The mean of their marks. 4.9
b) The mean of their marks, when the marks of each students are increased by 3. 7.9
8) The mean of five number is 18. On excluding one number, the mean become 16. Find the excluded number. 26
20/10/24
1) The shadow of a flag post 25m high is 25√3m. Find th
e angle of elevation of the Sun.
2) A conical tent has a circular base of area 0.375 hectres. If its height is 20m, find its capacity.
3) The sum of two radii of two circles is 18.5cm and the difference of their circumference is 22cm. Find the radius of the bigger circle.
4) OX and OY are the co-ordinate axes.AB= 6cm. The point A slides along OX and point B slides along OY. Find the locus of the midpoint of AB.
6) In the figure,E is the midpoint of AC and BE Perpendicular AC. AX bisects angle BAC meeting BC at D and BE at Y. Prove that
a) the point Y is equidistant from A and C.
b) the point D is equidistance from AB and AC.
7) The line x - y = 3 divides the join of (3,4) and (8,3) in the ratio m: n. Find the ratio.
8) The ordinate of a point P is greater than its abscissa by 3 units. Its distance from a point A(-4,-8) is 17 units. Find the coordinates of the point P if it lies in the first quadrant.
9) If A= 2 0 & B= 14 0
-3 4 -45 44 find the values of scalar factors x and y, such that xA²+ yA = B.
10) 4x³- 12x²+ ax + b has x -3 is a factor but when it is divided by x + 2 the remainder is -75, find a and b.
11) A's income is Rs140 more than B's and C's income is Rs80 more than D's. If the ratio of A's and C's income is 2:3 and the ratio of B's and D's income is 1:2, find the income of each.
12) A function f is defined as a set of integers,
f(x)= 2x+5, 2< x ≤ 4
3x -4, 0< x≤ 2
a) Find f and the domain and range of the function
b) Can you find f(1/3). If not , why?
13) Three numbers are in continued proportion. Their sum is 38 and the sum of their squares is 532. Find the numbers.
14) Mrs. Mehta plans to invest Rs 8456 in shares. She partly investos in 17% shares at Rs 140 and the remaining amount in 9% shares at Rs112. Her income from the second investment is Rs58 more than the first investment. How much did she invest in shares at Rs112?
15) if the loan is returned after 1 year, a person would have to pay Rs6240 only. If it is returned after 2 years he would have to pay Rs6489.60 with compound interest . Calculate the amount of loan and the rate of interest.
16) Bhagat deposits Rs1500 every month for 36 months in a bank and receives Rs65655 at the end of 36 months. Find the rate of simple interest paid by the bank on the recurring deposit.
17) Solve the inequation and represent it on the number line x/2 + 3 ≤ x/3 + 4 < 4x -7, x belongs to R.
18) Find the value of x and y if
A= x+ y y B= 2 & C= 3
2x x-y -1 2 with the relation AB = C
19) Abscissa of a point P is twice its ordinates. If the point P is equidistant from A(2, -5) and B(-3,6), find its coordinates.
20) From the following table, find the frequency distribution and calculate the mean marks
Marks no of students
less than 8 4
less than 16 10
less than 24 22
less than 32 41
less than 40 50
21) A man sold a briefcase at 8% profit. Had he purchased it for 10% less and sold it for the Rs72 less, he would have gained 50/3%. For how much did the man purchase the briefcase?
22) Prove sin⁶x + cos⁶x = 1 - 3 sin²x + 3 sin⁴x
23) A regular 10 sided polygon is inscribed in a circle of radius 20cm. Find each side of the polygon.
24) Two spheres of the same metal weight 1 kgf and 7kgf. The radius of the smaller sphere is 2.5cm. The Sphere are melted to form a single big sphere. Find the diameter of big sphere .
26) Two straight roads PQ and PR cross each other at P at an angle of 75°. S is a stone on the road PQ, 800 metres from P, towards Q. By drawing a figure to scale 1 cm = 100m, locate the position of a flagstaff X, which is equidistant from P and S and is also equidistant from X from P and calculate the actual distr.
27) ∆ ABC and ∆ PQR are similar and their areas are 1089 cm² and 2304cm² respectively. If AB = 22cm, find PQ.
28) if A(3,2), B(-2,4) and C(3,-2) are the vertices of ∆ ABC, find the equation of the line perpendicular to AB and passing through the mid point of BC.
29) The difference between the reciprocals of two consecutive multiples of 3 is 1/468. Find the numbers.
30) A man borrowed a certain sum of money. He can pay Rs242000 after 2 years or pay Rs292820 after 4 years to clear the debt alongwith compound interest. Find
a) the rate percent per annum.
b) The sum borrowed
16/10/24
1) Write down the first five terms of the sequence, whose nth term is (-1)ⁿ⁻¹. 5ⁿ⁺¹. 25,-125,625, -3125, 15625
2) If the third and the 6th terms of an AP are 7 and 13 respectively, find the first term and the common difference. 3, 2
3) Find the sum of all natural numbers between 100 and 1000 which are multiple of 5. 98450
4) How many terms of the AP -6, -11/2, -5, .... are needed to give the sum -25? 5 or 20
5) Determine the sum of the first 25 terms of an AP if a₂= 2 and a₇= 22. 2310
6) If the first term of an AP is 2 and the sum of first five terms is equals to the one fourth of the sum of the next 5 terms , show that the 20th term is -112.
7) Insert 3 Arithmetic mean between 2 and 10. 4,6,8
8) Find the 12th term of a GP, whose 8th term is 192 and the common ratio is 2. 3072
9) The first term of a GP is 1. The sum of the third and fifth terms is 90. Find the common ratio of the GP. ±3
10) The sum of first three terms of a GP is 39/10 and their product is 1. Find the common ratio and the terms. 2/5,1,5/2 or 5/2,1,2/5
11) The sum of some terms of a GP is 315 and the first term and the common ratio are 5 and 2 respectively. Find the last term and the number of terms. 6, 160
12) Find the sum of the series 0.6+0.66+0.666+..... to the n terms. 2n/3 -(2/27) (1- 10⁻ⁿ).
13) Insert 3 geometric mean between 1 and 256. 4,16,64
14) Find the sum 5²+ 6²+7²+.....+20². 2840
15) If in a geometric progression consisting of positive terms, each term equals the sum of the next two times. Then the common ratio of this progression equals.
a) √5 b) (1/2)(√5-1) c) (1/2)(1-√5) d) √5/2.
16) If fifth term of a GP is 2, then the product of its first 9 terms.
a) 256 b) 512 c) 1024 d) none
17) The sum of three decreasing numbers in AP is 27. If -1, -1, 3 are added to them respectively, the resulting series in GP. The numbers are
a) 5,9, 13 b) 15, 9, 3 c) 13,9, 5 d) 17, 9, 1
18) The sum of all odd numbers between 1 and 100 divisible by 3, is
a) 83667 b) 90000 c) 83660 d) none
10/10/24
TRIGONOMETRY
1) (cos³x + sin³x)/(cosx + sinx)+ (cos³x - sin³x)/(cosx - sinx)= 2.
2) cosA/(1- tanA) +
sinA/(1- cotA)= cosA + sinA.
3) sinA/(cotA + cosecA) = 2+ sinA/(cotA- cosecA)
4) sinx/(1+ cosx) + (1+ cosx)/sinx= 2cosecx.
5) √{(1+ cosx)/(1- cosx)}= cosecx + cotx.
6) 1/(sinx + cosx) + 1/(sinx - cosx)= 2sinx/(1- 2cos²x)
7) 1 - cos²θ/(1+ sinθ)= sinθ.
8) √{(1- cos θ)/(1+ cosθ)= sinθ/(1+ cosθ)
9) sin²θ(1+ cot²θ)= 1
10) (1- tan²θ)cos²θ= 1.
11) cot²A - 1/sin²A= 1
12) tan²θ/(secθ -1)= 1+ secθ
13) (secx -1)/(sex +1)= (1- cosx)/(1+ cosx).
14) cos²x + 2sinx cosx + sin²x = 1+ 2sinx cosx.
15) (sinx tanx)/(1- cosx)= 1+ secx.
16) (1+ cosx)(1- cosx)(1+ cot²x)= 1.
17) 1/(1+ sinx) + 1/(1- sinx)= 2sec²x
18) cosecx/(cosecx -1) + cosecx/(cosecx +1)= 2sec²x
19) sec²θ+ cosec²θ= sec²θ cosec²θ
20) tan²x - sin²x = tan²x sin²x.
21) sin⁴θ + sin²θ cos²θ = sin²θ
22) sin⁴x cosec²x + cos⁴x sec²x =1.
23) tan⁴x + tan²x = sec⁴x - sec²x.
24) cos⁴θ - sin⁴θ = 2 cos²θ -1.
25) (secx - cosx)(secx + cosx)= sin²x + tan²x
26) sec²x cosec²x = tan²x + cot²x +2.
27) 1/(cosecx + cotx)= cosecx - cotx
28) (secx + tanx)/(secx - tanx)= {(1+ sinx)/cosx}².
29) tan²θ/(secθ -1)² = (1+ cosθ)/(1- cosθ).
30) sinx/(1- cosx)= cosecx + cotx.
31) sin²x/(sinx - cosx) + cosx/(1- tanx)= sinx + cotx.
32) (secx - tanx)/(secx + tanx)= 1- 2secx tanx + 2 tan²x
33) tanA/(1- cotA) + cotA/(1- tanA)= secA cosecA +1.
34) (sinx - 2sin³x)/(2cos³x - cosx)= tanx.
35) (cotx + tany)/(cot y+ tanx)= cot x tany
36) sin²x cos²y - cos²x sin²y = sin²x - sin²y.
37) tan²x sec²y - sec²x tan²y = tan²x - tan²y.
38) √(secx + tanx) √(secx - tanx)= 1
39) √(sin²x+ cos²x + tan²x) = secx.
40) (cosA cosecA - sinA secA)/(cosA + sinA)= cosecA - secA
41) √{(1+ cosx)/(1- cosx) + √{(1- cosx)/(1+ cosx) = 2 cosecx.
42) √{(secx -1)/(secx +1) + √{(secx +1)/(secx -1) = 2 cosecx
43) (sinx + cosx)/(sinx - cosx) + (sinx - cosx)/(sinx +cosx) = 2/(1- 2 cos²x).
44) (tan²x - sec²x)/(cot²x - cosec²x)= 1.
45) (tanx + 1/cosx)²+ (tanx - 1/cosx)²= 2 {(1+ sin²x)/(1- sin²x)}
46) (cotx + cosecx -1)/(cotx - cosecx +1)= (1+ cosx)/sinx.
47) 1/(cosecx - cotx) - 1/sinx = 1/sinx - 1/(cosec x + cotx).
48) sin⁶x + cos⁶x = 1- 3 sin²x cos²x.
49) If sinx + cosx = m and secx + Cosecx = n then show n(m²-1)= 2m.
50) If x= r cosa sinb , y= r cos a cos b and z= r sin a, show x²+ y²+ z²= r²
51) If m= tanx + sinx and n= tanx - sinx show m²- n²= 4 √(mn).
52) m= cosx/cos y and n= cosx/sin b, show (m²+ n²) cos²y = n².
53) If a secx + b tanx = m and a tanx + b secx = n, show that m²- n²= a²- b²
54) If cosx + sinx =√2 cosx, show cosx - sinx =√2 sinx.
1) If 2cosx = 2/5, find sinx.
2) If sinx =3/5 and cosy = 12/13, evaluate
a) sec²x
b) tanx + tany.
3) If 2 sinx -1=0, show that sin3x = 3sinx - 4 sin³x
4) Given 5cosx - 12x = 0 then find (sinx + cosx)/(2cosx - sinx).
5) Given A is an acute angled and 13 sinA = 5, evaluate (5sinA- 2cosA)/tanA.
6) If cosx = 5/13, find sinx, tanx. Cotx, cosecx.
7) If sinx = 4/5 then find the value of secx + cotx
8) If 3tanx = 4, find the value of (sinx tanx -1)/2tan²x.
9) If tany = 3/4, find the value of (4siny - 2cosy)/(4siny + 3cos y).
10) If 2 sinx = 1, find(tanx + cotx)².
11) If cosx = 1/25, show (1- cos²x)/(2- sin²x)= 3/5.
12) Solve:
a) sinx = cosx.
b) 2sin²x = 1/2.
c) 2cos²x -1=0
d) 4tan²x = 12.
1) tan10 tan20 tan30 tan70 tan80= 1/√3
2) sinx/sin(90-x) + cosx/cos(90-x)= sec(90- x) cosec(90- x)
3) (sin²20+ sin²70)/(cos²20+ cos²70) + (sin(90-x) sinx)/tanx + (cos(90-x) cosx)/cotx= 2.
4) 14 sin30+ 6 cos60 - 5 tan45
5) cos75/sin15 + sin12/cos78 - cos18/sin72.
6) 3 cos80 cosec10 + 2 cos59 cosec31
7) sec²27- cot²63.
8) sin(90- x) cos(90- x)= tanx/(1+ tan²x).
9) 1- (cosx cos(90- x))/cotx = cos²x.
10) cosx cos(90-x)- sinx sin(90- x)= 0
11) sin(90-x) cos(90- x)= tanx cos²x.
12) cos(65+ x)- sin(25- x)= 0
13) sin(50+ x) - cos(40- x)= 0
14) (sin(90-x) cos(90-x))/tanx = 1- sin²x.
15) sin(90- x) cos(90- x)= tanx/(1+ cot²(90- x)).
16) (sinx cos(90-x) cosx)/sin(90-x) + (cosx sin(99- x)/cos(90- x)= 1
17) cosec²(90- x) - tan²x = cos²(90- x)+ cos²x.
18) cot(90- x)/(1+ tan(90-x)) + tan(90-x)/(1- cot(90-x))= secx cosecx +1.
19) (cos(90-x) sec(90- x) tan(99-x) cot(90-x))/(sun²(90-x)+ cos²(90-x))= 1
20 If A, B, C interior angles of ∆ ABC prove that
a) sin{(B+ C)/2}= cos(A/2).
b) tan {(A+ B)/2} = cot(A/2).
9/10/24
Arithmetic progression
1) The mth term of the AP 5, 11, 17, 23,.... is
a) 6m - 1 b) 6m +1 c) 5m -1 d) 6n -1
2) If nth term of an AP is 2n-1, then its 20th term is
a) 33 b) 34 c) 36 d) 39
3) The number of terms in the AP 7, 16, 25,.... 349 is
a) 40 b) 39 c) 38 d) 35
4) The sum of first 8 multiples of 3 is
a) 108 b) 100 c) 96 d) 95
5) If the nth term of an AP is Tₙ= 5 - 3n, then its common difference is
a) -2 b) -3 c) 3 d) 4
6) The first term of the AP whose pth term is 3p - 1 is
a) 2 b) 3 c) 4 d) 5
7) The 10th term of the AP 120, 116, 112 ....is
a) 80 b) 82 c) 84 d) 90
8) The common difference of the AP - 15, - 12, - 9, .... is
a) 3 b) - 3 c) 2 d) - 2
9) if the sum of the first n terms of an AP is given by Sₙ= -5n +1. The common difference of the AP is
a) -8 b) 8 c) 7 d) -1
10) The nth term of an AP is given by Tₙ = -5n +1. The common difference of the AP whose is
a) -5 b) -4 c) 4 d) -2
11) For an AP, if a= 5, d= 3 and tₙ = 50, then the value of n is :
a) 10 b) 16 c) 20 d) 21
12) The sum of the first 6 multiple of 5 is
a) 100 b) 102 c) 104 d) 105
13) Which term of the AP 4, 9, 14, 19.... is 124 ?
a) 20th b) 22nd c) 24 th d) 25th
14) The 10th term from the end of the AP -2, -6, -10,....-110 is
a) -72 b) 74 c) -74 d) -70
15) If (5m+2), (4m -1) and (m +2) are in AP, then the value of m is
a) 1 b) 2 c) -1 d) 3
16) The 11th term of the AP -3, -1/2, 2.... is
a) 22 b) 21 c) 20 d) 16
17) The common difference of the AP whose pth term is 8p+1, is
a) 1 b) 4 c) -7 d) 8
18) The nth term of the AP 2, 5, 8, ..... is
a) 3n+1 b) 2n -1 c) 2n+3 d) 3n -1
19) The 100th term of the AP x, x+1, x+2,.... is
a) 99 b) x c) x + 99 d) x - 99
20) The 6th term from the end of the AP 17, 14, 11,.... -40 is
a) 25 b) -25 c) -20 d) 40
SHORT QUESTIONS
1) Find the 16th term of the AP 7, 11, 15, 19 ..... Also find the sum of the first 6 terms.
2) The 2nd and 45th term of an arithmetic progression are 10 and 96 respectively . Find the first term and the common difference and hence find the sum of the first 15 terms.
3) if the 6th term of an AP is equal to four times its first term and the sum of first six term is 75, find the first term and the common difference.
4) Which term of the AP 3, 15, 27, 39...... will be 120 more than 21st term?
5) For what value of n, are the nth terms of two AP's 63, 65, 67,.... and 3, 10,17,... equal ?
6) Find the 20th term from the end of the AP 3, 8, 13,..... 253.
7) The first and last term of an AP are 5 and 45. If the sum of the terms is 400, find the number of the terms and the common difference.
8) Find the sum of the first 17 terms of an AP whose 4th, and 9th terms are -15 and -30 respectively.
9) Find the sum of odd numbers between 0 and 50.
LONG QUESTIONS
1) In an arithmetic progression (AP) the 4th and 6th terms are 8 and 14 respectively. Find the
a) first term
b) common difference
c) sum of the first 20 terms.
2) Find the value of the middle most term/s of the AP -11, -7, -3,....49.
3) If m times the mth term of an AP is equal to n times the nth term show that (m + n)th term of the AP is 9.
4) If the sum of first 7 terms of an AP is 49 and that of the 17 term is 289, find the sum of the first n terms .
5) The sum of the first 16 terms of an AP is 112 and the sum of its next 14 terms is 518. Find the AP.
6) If the first term of an AP is 2 and the sum of the first five terms is equal to one fourth of the sum of the next five terms, then
a) show that t₂₀ = 112
b) find the sum of first 30 terms.
7) How many terms of the AP 17,15,13..... must be added to get the sum 72? Explain the double answer.
8) If the pth, qth, and rth terms of an AP be a, b and c respectively, then show that a(q - r)+ b(r - p)+ c(p - q)= 0
8/10/24
QUADRATIC EQUATION
TYPE -1
1) 8x²+15=26x. 5/2,3/4
2) x(2x +5)=25. -5, 5/2
3) (x -3)/(x+3) + (x +3)/(x-3) =5/2, x≠-3, x≠ 3. 9,-9
4) 2x -3= √(2x²- 2x +21. 6
5) (x²-5x)/2= 0. 0,5
6) 3x +35= 2x². 5, -7/2
7) 6x²+ x = 35. -5/2,7/3
8) 6x(3x -7)= 7(7- 3x). 7/3,-7/6
9) 3(y⅖-6)= y(y+7)-3. 5, -3/2
10) x²- 4x -12=0, when x belongs to N. 6
11) 2x²- 9x +10=0, when a) x∈N b) x ∈Q. 2, 2 and 5/2
12) a²x²+ 2ax +1=0, a≠ 0. -1/a, -1/a
13) 1/x - 1/(x +2)= 1/24. -8,6
14) (x +1)/(x-1) = (3x -7)/(2x-5). 3,4
15) (3x +1)/(7x+1) = (5x +1)/(7x+5). 1,-2/7
16) 5/(2x +1)+ 6/(x+1) = 3. 2,-2/3
17) (x +3)/(x-2) - (1- x)/x = 17/4. 4,-2/9
18) a/(ax -1)+ b/(bx-1) = a+ b, a+ b≠ 0, ab≠ 0. (a+ b)/ab, 2/(a+ b)
19) 2²ˣ⁺³ - 9. 2ˣ +1= 0. 0,-3
20) Frame the quadratic equation whose roots are:
a) -2,1. x²+ x -2=0
b) -3,-4. x²+7x +12=0
c) a,-b. x²-(a - b)x - ab=0
d) -2/3, 4/5. 15x²- 2x -8=0
e) -3,2/5. 5x²+ 13x -6=0
TYPE -2
1) 3x²- x -7= 0 (two decimal places. 1.70 or -1.37
2) 1/(x +1) + 2/(x+2) = 4/(x +4).
3) 3/(x+1) - 1/(x +2) = 1/(x+3). Two decimal places. -2.27 or -5.73
4) 2(3x²-1)= x. 2/3,-1/2
5) (x +3)/(2x+3) = (x +1)/(3x+2). (-3+√6),(-3-√6)
6) (x -2)/(x+2) + (x +2)/(x-2) = 4. 2√3,-2√3
7) 1/(x +2)+ 2/(x+2) = 4/(x +4). (2+2√3),(2-2√3)
8) a(x²+1)= (a²+1)x, a≠ 0. a, 1/a
9) 4x²- 4ax - (a²- b²)= 0. (a+b)/2, (a- b)/2
TYPE -3
1) An Aeroplane travelled a distance of 400 km at an average speed of x kmph . On the return journey the speed was increased by 40 kmph. Write down an expression for the time taken for:
a) the onward journey
b) the return journey
If the return journey took 30 minutes less than the onward journey, write an equation in x and find the value of x.
2) Ca A travels x km for every litres of petrol, while car B travel (x+5) km for every litre of petrol.
a) Write down the number of litres of petrol used by car A and car B in covering a distance of 400 km.
b) If car A uses 4 liters of petrol more than car B in covering the 400 km. Write down an equation in terms of x and solve it to determine the number of liters of petrol used by car B for the journey.
3) In an auditorium, seats were arranged in rows and columns. The number of rows was equal to the number of seats in each row. When the number of rows doubled and the number of seats in each row was reduced by 10, the total number of seats increased by 300. Find :
a) the number of a rows in the original arrangement.
b) the number of seats in the auditorium after rearrangement.
4) a hotel bill for a number of people for overnight stay is Rs4800. If there were 4 people more, the bill each person had to pay would have a reduced by Rs200. Find the number of people staying overnight.
5) A trader buys x articles for a total cost of Rs600.
a) write down the cost of 1 articles in terms of x.
If the cost per article were Rs 5 more, the number of articles that can be bought for Rs600 would be four less.
b) write down the equation in x for the above situation and solve it for x.
6) A train covers a distance of 600 km at x kmph . Had the speed been (x+20) kmph, the time taken to cover the distance would have been reduced by 5 hours. Write down an equation in terms of x and solve it to evaaluate x.
7) The sum of two number is 18 and their product is 56. Find the numbers .
8) The cost of 2x articles is Rs(5x + 54) while the cost of (x + 2) articles is Rs(10-4). Find x.
9) The difference of the square of two numbers is 45. The square of the smaller number is 4 times the larger number. Determine the numbers.
10) There are three consecutive positive integers such that the sum of the square of the first and the product of other two is 154. What are the integers.
11) A years ago the father was 8 times as old as his son. now his age is the square of his son's age. Find their present ages.
12) The length of a rectangle exceeds its width by 8cm and the area of the rectangle is 240 sq.cm. Find the dimensions of the rectangle.
13) The area of right angled triangle is 600 sq.cm. if the base of the triangle exceeds the altitude by 10cm, find the dimension of the triangle.
14) The length of the hypotenuse of a right-angle exceeds the length of the base by 2cm and exceeds twice the length of the attitude by 1cm. Find the length of each side of the triangle.
15) Two squares have sides x cm and (x + 5)cm. The sum of their areas is 697sq.cm.
a) Express this as an algebraic equation in terms of x.
b) solve this equation to find the sides of the squares .
16) The sum of the numerator and denominator of a fraction is 8. If 1 is added to both the numerator and denominator, the fraction is increased by 1/15. Find the fraction.
17) Rs 6500 were divided equally among a certain number of persons. Had there been 15 more persons, each would have got Rs30 less. Find the original number of persons .
18) A piece of cloth costs Rs200. If the piece were 5 m longer, and each metre of cloth cost Rs 2 less, the cost of piece would have remained unchanged . How long is the piece and what is its original rate per metre ?
19) The length of a rectangle is 8 metres more than its breadth and its area is 425m².
a) taking x metres as the breadth of the rectangle, write an equation in x that represents the above statement.
b) solve the above equation and find the dimensions of the rectangle.
20) The perimeter of a rectangle plot of land is 114 m and its area is 810 square metre.
a) take the length of the plot as x metres . Use the perimeter and 114m to write the value of the breadth in terms of x.
b) use the values of length, breadth and area to write an equation in x.
c) solve the equation to find the length and breadth of the plot.
21) Rs6400 were divided equally among x persons. Had this money been divided equally among (x +14) persons, each would have got Rs28 less. Find the value of x.
22) A shopkeeper buys x books for Rs720.
a) write the cost of one book in terms of x.
b) if the cost per book were Rs5 less, the number of books that can be bought for Rs720 were 2 more. Write down the equation in x for the above situation and solve it to find x.
23) A fruit bought x apples for Rs1200.
a) write the cost price of each apple in terms of x.
b) if 10 of the apples were rotten and he sold each of the rest of Rs3 more than the cost price of each, write the selling price of (x-10) apples.
c) if he made a profit of Rs60 in this transaction, from an equation in x and solve it to find x.
24) An aeroplane flying with a wind of 30kmph takes 40 minutes less to fly 3600 km, than what would have taken to fly against the same wind. Find the plane's speed of flying in still air.
25) Some students planned a picnic. The budget for food was Rs500. But 5 of these failed to go and thus the cost of the food for each member increased by Rs5. How many students attended the picnic ?
26) One pipe can fill a cistern in 3 hours less than the other. The two pipes together can fill it in 6 hours 40 minutes. Find the time that each pipe will take to fill the cistern.
27) In a flight of 2800km, an aircraft was slowed down due to bad weather. Its average speed for the trip was reduced by 100 kmph and timing increased by 30 minutes. Find the original duration of light.
28) Two circles touch externally. The sum of their areas is 130π cm² and the distance between their centres is 14cm. Find the radii of the circles.
4/10/24
FILL IN THE BLANKS
2) The roots of the quadric equation ax²+ 2bx + c=____(a≠0) are real and equal, then b²= _____.
2) The equation (a- 2)x²+ 3x +5=0 will not be a quadratic equation for a=___.
3) In in quadratic equation ax²+ bx + c=0(a≠ 0), b²= 4ac, then the roots of the equation will be real and ____.
4) a: 2= b :5 = c: 8 then , a 50%= b 20% = c_____%.
5) if the sum and product of two quadratic conditions is a fundamental number, then both the conditions are____.
6) (x -2) and (x -3) is proportional x to the mean of the x____.
7) 7x²- 12x +18=0. The ratio of the sum and the product of the roots of the equations_____.
8) ax²+ bx + c=0 (a≠0) if both the roots of the equation are mutually inverse (reciprocal), then c=____.
9) ax²+ bx + c=0 (a≠ 0) if both the roots of the are mutually inverse and negative, then a+ c=____.
11) The product of three consecutive proportional positive numbers is 64, the proportional between them is ____.
12) If sum of two angles is ___, then they are called supplementary angles.
13) If the bases of two triangles are situated on same line and the other vertex of the two triangles are common, then the ratio of the areas of two triangles are ____ to the ratio of their bases.
14) if ABCD is a cyclic parallelogram then angle A is____.
15) If the length of the sides of two Triangles are in proportion, then two Triangles are _____.
16) If both the angles made by an arc in the same arc are equal, then the length of both the arcs is ____.
17) A contagious Parallelogram is a_____.
14) The vertices of a square figure are ____.
15) If a straight line intersects a cut at two points, then the straight line is called the ___ of the cut.
16) Due to the ratio of the length of the two chords PQ and RS in the O central circle, 1:1 angle POQ: angle ROS= ____ .
17) the perpendicular bisector of a chord of a chord is____.
18) Angles lying in the same verse are ____.
19) If the line segment joining two points makes equal opposite angles to the other two points on the same side, then the four points will be____.
20) Two Triangles are similar if their____
21) If a straight line intersects the circle at two points, then the straight line is called ____ of circle.
22) Two circles touch each other externally at the point A. A common tangent drawn to the two circles at the point A is ____ common tangent (direct/ transverse).
23) if AOB is the diameter of a circle and C and D are two different points on the circumference not on the same side of AB, such that angle AOC=130°, then the value of angle CDB will be____.
24) The line segment parallel to any side of a triangle divides other two sides or the extended two sides ___.
25) The perpendicular bisector of any chord of a circle is____ of that circle.
26) The angle in the segment of a circle which is less than the semicircle is an ____angle.
27) three circles can intersect each other at more than ____point/s.
28) The distance between the centres of two circles with radii 9cm and 16cm is 25cm. The length of the segment of the tangent between them is____cm.
29) In ∆ ABC , angle A= angle B= 60°, AC=8cm. The lines AD and BD intersect at D with D= 90°. If DB= 2cm then the length of AD is ____cm.
30) If an exterior angle of a cyclic quadrilateral be 50°, then the interior opposite angle is____.
31) If PQ is the diameter of a circle with centre O and R is a point on the circumference such that angle ROQ= 120°, then the value of angle ORP is ____.
32) The circle drawn with the hypotenuse of a right angled triangle as diameter passes through the ____.
33) The straight lines parallel to the parallel sides of a trapezium divides____ other two sides.
34) If cos²x - sin²x = 1/x (x > 1), then cos⁴x - sin⁴x = ____.
35) If the sun's angle of elevation increases from 30° to 60°, the length of the shadow of a post____. (decreases/ increases).
36) if the angle of elevation of the sun is 45°, then the length of shadow and length of post ate____.
37) If the opposite angles of a quadrilateral be supplement then the vertices of the quadrilateral will be_____.
38) The value of (4/sec²x + 1/(1+ cot²x) + 3 sin²x) is ____.
39) The vertical of a cyclic squares are _____.
40) One solid sphere is melted and a solid right circular cylinder is made, then _____ of sphere and the cylinder will be equal.
42) number of surfaces of the solid right circular cylinder is____.
43) The shape of a pencil with one end sarpend is the combination of a cylinder and a ____.
44) The numbers are plane surface of a solid hemisphere are____.
45) ABC is the hypotenuse of the right angle AC triangle. Considering the side AB as an axis, the diameter of the right circular cone that will be formed in full circle of the triangle will be____.
46) if the volume of a right circular cone is V cubic units and the area of the base being A square units, the height will be_____.
47) If the radius of the base of a right circular cylinder and a right circular cone are the same and their heights are also be same, then the ratio of their volumes will be ____.
48) A solid sphere is melted to form a solid right circular cylinder. The volume of the sphere and the cylinder is____.
49) The number of diagonals of a rectangular solid is____.
50) The length of the diagonal of a plane of a cube= ____ x length of one side.
51) A rectangular paper has unit length and unit width . A rectangular paper is folded into cylinder whose circumference is equal to the length of the paper____ curve of cylinder.
52) The length of the radius of the base of a solid right circular cylinder and two hemisphere are equal. If tor hemisphere are placed side by side with the plane of the cylinder, then what is the shape of the new solid object = area of the plane of a hemisphere + ____ area of the curve of+ The area of the curve of second hemisphere.
53) If the diameter of a circular pipe is 3 cm and height is 4cm, then the length of the longest pole that will be placed inside the pipe is_____ cm.
54) If the volume of a right circular cylinder and the area of the curved plane have the same number of values, then the length of the diameter of the cylinder is____.
55) The variable x₁, x₂,.......x₁₀₀ are in ascending order of their magnitude, then the median of the variable is____.
56) The measured of central tendency are mean, median and____.
57) if the mean x₁, x₂, x₃....xₙ be bar x, then the mean of kx₁, kx₂, kx₃....kxₙ is _____(k≠0).
58) The median of the data 8, 9, 6, 7, 5, 6, 7, 8, 9, 10 is____.
59) If the mean of the number 6, 7, x, 8, y, 14 is 9, then x + y=____.
60) The relation between x and y is 2x + 3y=7. If the median of y is 2; then the median of x is _____.
61) The median of 2, 3, 4, 3, 6, 7, 8 is ____.
62) The following are the marks obtained by 10 students in physics test: 65, 52, 71, 47, 49, 51, 37, 29, 77, 62; then the mean mark is____.
63) The mode of 2, 3, 5, 6, 2, 4, 2, 8, 6, 9 will be____.
64) The mode of the data 1,1,2,2,2,3,3,3,4,4,5,6,7 is____.
CHOOSE THE CORRECT OPTION:
1) The product of two roots of the equation x²-7x +3 =0 is
a) 7 b) -7 c) 3 d) - 3
2) Under what condition one root of the quadric equation ax²+ bx + c=0 is zero ?
a) a= 0 b) b= 0 c) c= 0 d) none.
3) 2x²- 3x - k +2=0 one root of the equation is 0. The value of k is
a) 2 b) -2 c) 1/2 d) -1/2
4) The mean proportional of 9 and 25 is
a) 20 b) 21 c) 41 d) 441
5) If two roots of equation x²+ 4x +k=0 are equal, then the value of k is
a) 1 b) 2 c) 3 d) 4
6) If two roots of equation x²- 6x + k=0 are real and unequal then what is the value of k ?
a) more than 6 b) less than 6 c) more than 9 d) less than 9.
7) The sum of two roots of the equation x²- 6x +2=0
a) 2 b) - 2 c) 6 d) - 6
8) If the product of two roots of the equation is x²- 3x + k=10 is -2, what is the value of k ?
a) - 2 b) - 8 c) 8 d) 12
9) If two roots of the equation ax²+ bx + c=0(a≠ 0) be equal , then
a) c= -b/2a b) c= b/2a c) c= - b²/4a d) c= b²/4a
10) The roots of the equation x²= 6² is/are
a) 0 b) 6 c) 0 and 6 d) - 6
11) if two roots of the equation (k +1)x²+ 2kx + (k +2)= 0 are equal and negative then the value of k is
a) 1 b) -1 c) 0 d) -2
12) If the roots of the equation ax²+ bx + c=0(c ≠ 0) are real and unequal then b²- 4ax will be
a) >0 b) =0 c) <0 d) none.
13) The number of roots in a quadratic equation is
a) 1 b) 2 c) 3 d) none.
14) If ax²+ bx + c=0 is a quadratic equation then
a) b≠ 0 b) c≠ 0 c) a≠ 0 d) none.
15) The highest power of the variable of a quadratic equation is
a) 1 b) 2 c) 3 d) none
16) The equation 4(5x²- 7x +2)= 5(4x²- 6x +3) is
a) linear b) quadratic c) 3rd degree d) none
17) third proportion of 8 and 12 is
a) 12 b) 16 c) 18 d) 20
18) a is a positive number and if a: 27/64 = 3/4: a, then the value of a is :
a) 81/256 b) 9 c) 9/16 d) 16/9 c
19) The length of the two chords AB and CD cycle of a circle of centre O are equal and angle AOB= 60°,
a) 40° b) 30° c) 60° d) 90°
20) O is the centre of a circle and AB is a diameter, ABCD is a the cyclic quadrilateral.Angle ABC=65°, angle DAC= 40°, then the measure of angle BCD is
a) 75° b) 105° c) 115° d) 80° c
21) If Angle A =100° of a cyclic quadrilateral ABCD, then the value of angle C is
a) 50° b) 80° c) 180° d) 200°
22) The number of common tangents of two circles when they do not touch or intersect each other is :
a) 2 b) 1 c) 3 d) 2
23) The length of the radius of 6 circle is 13cm and the length of a chord of the circle is 10cm, the distance of the coord from the centre of the circle is
a) 12.5cm b) 12 cm c) √69cm d) 24 cm
24) The centre of two concentric circles is O; a straight line intersects a circle at point A and B and the other circle at point C and D. If AC= 5 cm, then the length of BD is
a) 2.5cm b) 5cm c) 10 cm d) none.
25) The distance between two parallel chords of length 8cm each in a circle of diameter 10 cm is
a) 6cm b) 7cm c) 8cm d) 5.5 cm
a) 70° b) 60° c) 40° d) 200°
27) In the adjoining figure,if O is the centre of the circle and the BC is the diameter then the value of x is
a) 60° b) 50° c) 100° d) 80°
28) In the adjoining figure,O is the centre of the circle; if ang ACB =30°, angle ABC= 60°, angle DAB= 35° and DBX= x°, then the value of x is
a) 35 b) 70 c) 65 d) 55
29) If AB is a diameter of a circle with Centre O and C is a point on the circumference such that angle BOC=60°, then the value of angle AOC is
a) 60° b) 30° c) 120° d) 90°
30) In the adjoining figure,O is the centre of the circle and AB is the diameter. If AB || CD, angle ABC=25°, then the value of angle CED is
a) 80° b) 50° c) 25° d) 40°
31) In the adjoining figure,
a) 56° b) 86° c) 38° d) 28°
32) In the diagrambesides O is the centre of the circle and AB is a diameter. ABCD is a cyclic quadrilateral. Angle BAC is
a) 50° b) 60° c) 30° d) 40°
33) In the diagrambesides ABCD is a cyclic quadrilateral. BA is produced to the point F. If AE|| CD, angle ABC= 92° and angle FAE= 20°, then the value of angle BCD is
a) 20° b) 88° c) 108° d) 72°
34) I is the centre of ∆ ABC, angle ABC= 60° and angle ACB= 50°. Then angle BIC is
a) 55° b) 125° c) 70° d) 65°
35) In the adjoining figure,O is the centre of the cirle, if Angle BAD= 65°, angle BCD= 45°, then the value of angle BCD is
a) 65° b) 45° c) 40° d) 20°
36) If tanx + cotx =2, then the value of (tan¹³x + cot¹³x) is
a) 1 b) 0 c) 2 d) none
37) If 2x = secA and tanA= 2/x then the value of 2(x²- 1/x²)²= ?
a) 1/2 b) 1/4 c) 1/8 d) 1/16
38) Height of tower is 100√3 metres. The angle of elevation of the top of the tower from a point at a distance 100metres from the foot of the tower is
a) 30° b) 45° c) 60° d) none
39) If the ratio of the volume of two right circular cones is 1:4 and the ratio of radii of their bases is 4:5, then the ratio of their height is:
a) 1:5 b) 5:4 c) 25: 16 d) 25 :64
40) If each of radius of the base and height of a cone be doubled, then the volume of it will be
a) 3 times b) 4 times c) 6 times d) 8 times
41) If the height of a cone is h unit, slant height I units and the diameter of the base is d unit, then (l²- h²)/d²= ?
a) 1/2 b) 1/3 c) 1/4 d) 1/5
42) If the ratio of the radii of two circular solid cylinder 2 :3 and the ratio of their height is 5:3, then the ratio of the areas of their sides is
a) 2:5 b) 8 : 7 c) 10:9 d) 16:9
43) if the ratio of the radiu of two right circular solid cylinder is 2:3 and that of the height is 5:3, then the ratio of their volume is
a) 27:20 b) 20: 27 c) 4 :9 d) 9 :4
44) 2 right circular cylinders have equal volumes and the ratio of their heights is 1:2, then the ratio of their radii--
a) 1:√2 b) √2: 1 c) 1:2 d) 2:1
45) If the radius of a right circular cylinder is half the length and twice the height, then the volume of the cylinder will be the volume of the initial cylinder.
a) equal b) double c) half d) four times
46) when the radius of a right circular cylinder is doubled and the height is halved , the area of the circle is the area of the original cylinder.
a) equal b) double c) half d) four times.
47) If the ratio of the volumes of two solid sphere is 1:8, then the ratio of the area of the sphere will be ---
a) 1:2 b) 1:4 c) 1: 8 d) 1:16
48) The total surface area of a solid hemisphere of radius 7cm will be
a) 588π sq.cm b) 392π sq.cm c) 147π sq.cm d) 98π sq.cm
49) if the ratio of the areas of the sides of two solid sphere is 16:9, then the ratio of their volumes will be
a) 64 :27 b) 4 :3 c) 27 :64 d) 3:4
50) if the area of the circle of a solid sphere and three times the volume have the same numerical value, then the length of the radius of the sphere is
a) 1 unit b) 2 unit c) 3 units d) 4 units.
51) If the slant height of a right circular cone is 15cm and the diameter of the base is 16cm, then the area of the lateral plane of the cone will be
a) 60π sq.cm b) 68π sq.cm c) 120π sq.cm d) 130 π sq.cm
52) The ratio of the volumes of two right circular cones is 1:4 and the radius of their bases is 4:5 p, then the ratio of their heights will be
a) 1:5 b) 5:4 c) 25:16 d) 25:64
53) Keeping the radius of the base of a right circular cone the same and doubling its height, the increase in its volume will be
a) 100% b) 200% c) 300% d) 400%
54) if the radius of a right circular cone is r/2 units and the slant height is 21 units , then the area of the total plane of the cone is
a) 2πr(l+ r) cu. unit
b) πr(l+ r/4) cu. unit
c) πr(l+ r) cu. unit
d) 2πr cu. unit
55) The median of the data 11 , 29, 17, 21, 13, 31, 39, 19 is
a) (19+29)/2 b) 19 c) 21 d) none
56) Mode is the
a) least frequent value
b) middle most value
c) most frequent value
d) largest value
57) The mode of the data 1, 2, 3, 4, 5, 6, 7 is
a) 4 b) 6 c) 7 d) none
58) median of a frequency distribution can be obtained from
a) pie diagram
b) histogram
c) frequency polygon
d) ogive
59) The median of 1, 5, 9, 3, 8, 7 is
a) 5 b) 7 c) 8 d) 5 and 7 both
60) if the median after arranging in ascending order the data 8, 9, 12, 17, x+ 2, x + 4, 30, 31, 34, 39 is 15, then the value of x is
a) 22 b) 21 c) 20 d) 24
PROBABILITY
1) A fair die is thrown once. Find the probability that the number on it is :
a) an odd number
b) greater than 4.
c) at the most 4.
d) between 7 and 10.
2) Two fair coin are tossed. Find the probability that:
a) head turns up exactly once.
b) Tail turns up at least once.
c) Tail does not turn up at all.
3) A coin is tossed thrice. Find the probability that
a) Tail turns up atleast twice.
b) Head does not turn up at all.
c) Tail comes on the second toss.
d) head turns up atleast once.
4) Two fair dice are tossed. Find the probability that
a) The sum of the schore is 9.
b) the product of the score is 12.
c) the score on the second die is greater than the score on the first die.
d) the sum of the scores is a prime number.
e) the sum of the scores is a multiple of 4.
f) the sum of the score is a perfect square.
5) One card is drawn from a pack of well-shuffled pack of cards. Find the probability that the card drawn is:
a) A queen.
b) not a queen
c) A face card
d) red card
e) bears a number less than 4
f) king or black card
6) In a match between A and B, the probability of winning of A is 0.43. What is the probability of winning of B ?
7) A bag contains 3 red, 4 white, 5 blue marbles. All the marbles are identical in shape and size. One marble is drawn at random from the bag. Find the probability that the marble drawn is:
a) red
b) red or white
8) An unbiased coin is tossed. Find the probability that :
a) A head turns up.
b) A tail turns up
c) both head and tail turns up.
d) never head nor tail turns up.
9) A uniform die is thrown. Find the probability of the event A, B, and E where.
a) A= score is an even number
b) B= score is a number less than 5 but not less than 2.
c) score is a number that is a multiple of 3 or 5.
10) A perfect cubic die is thrown. Find the probability that
a) A prime number comes up
b) A perfect square comes up.
11) Two coins are tossed simultaneously. Find the probability of getting exactly one head.
12) 3 coins are tossed simultaneously. Find the probability getting at least one head.
13) Three unbiased coins are tossed. Find the probability of getting atleast two heads up.
14) A coin is tossed three times. Write the sample space. Find the probability of
E₁: getting two or more heads. E₂: the second is not a head.
15) Two unbiased dies are thrown in the air. find the probability that the sum of the scores is a multiple of 3.
16) Two dice are thrown. What is the probability that the sum of the points obtained is greater than 4 ?
17) Two unbiased dies are thrown. Find the probability that the sum of the numbers on their faces is at most five.
18) two fair die are thrown. Find the probability of getting the same score on the first die as on the second.
19) two unbiased dice are thrown in the air. Find the probability that the sum of the scores is greater than 9 or an even number.
20) if two pair die are thrown , find the probably that the sum of the points on their uppermost face is the perfect square or a multiple of 3.
21) a box contains 5 red, 11 white and 7 black balls. One ball is drawn at random. Find the probability that the ball drawn is a white ball.
22) A bag contains 6 red, 5 blue, 3 white and 4 black balls. A ball is drawn at random. Find the probability that the ball is red or black.
23) In a bag there are 6 black, 4 white and 3 yellow balls. A ball is taken at random. find the probability of getting a yellow or a white ball.
24) A box contains 7 red, 5 white and 8 green balls identical in all respects except colour. One ball is drawn at random. Find the probability that it is not white .
25) a card is drawn from a pack of well 52 playing cards. Find the probability that the card is drawn is
a) a diamond
b) a red card
c) A king
d) an ace or a queen
e) a face card
f) a card bearing number between and including 2 and 6.
26) six token bearing numbers 1 to 6 are placed in one box and seven tokens bearing number 1 to 7 are placed in another box. if one token is drawn from each box, what is the probability that the sum of the number is
a) 6
b) 11
27) If P(E)= 0.95, find P(not E).
28) A bag contains a certain number of the blue balls. A ball is drawn . Find the probability that the ball is black drawn is
a) black
b) blue.
29) The probability that two boys do not have the same birthday is 0.394. What is the probability that the two boys have the same birthday ?
30) Which of the following cannot be the probability of an event?
a) 5/7 b) 0.28 c) √2 d) -2.4
31) From a deck of 52 cards, all the face cards are removed and then the remaining cards are shuffled . Now one card is drawn from the remaining deck. Find the probability that the card is:
a) A black card.
b) 8 of red colour.
c) a king a black colour.
32) A box contains 1000 balls out of which 25 are defective. It is not possible to just look at the bulb and tell whether or not it is defective. One bulb is taken out at random from the box. Calculate the probability that the bulb taken out is
a) A good one
b) A defective one .
33) A bag contains 50 identical cards which are numbered from 1 to 50. If one card is drawn at random from the bag, find the probability that it bears
a) A perfect square number.
b) A number divisible by 4
c) A number divisible by 5
d) A number divisible by 4 or 5.
e) A number divisible by 4 and 5.
34) a bag contains 6 red, 8 white and x blue balls which are identical in shape and size. The probability that a ball drawn at random is blue or white is 5/7. Find x.
1) Rs100 shares of a company are selling at Rs80. If the company is paying a dividend of 12%, then the rate of return is:
a) 12% b) 15% c) 16% d) 18%
2) The roots of 3x²- 5x+1= 0 are
a) irrational b) equal c) imaginary d) none
3) On dividing x³- x²+ x -1 by (x -1), the remainder is:
a) 1 b) -1 c) 0 d) 4
4) A is a matrix of order 2x 3. The order of A' is
a) 2x3 b) 2x2 c) 3x 2 d) 3 x3
5) If the image of the point P under reflection in the x-axis is (3,4), then the coordinates of the point P are:
a) (3,4) b) (-3,-4) c) (3,-4) d) (-4,3)
a) 2cm b) 4cm c) 3.5 cm d) 2.5cm
7) If 2(x - 1)≤ 9, x ∈W, then the the greatest value of x is
a) 3 b) 2 c) 4 d) 5
8) which of the following can not be the probability of an event ?
a) 3/4 b) 3/5 c) 1.001 d) 0.6
9) If P( -1,1) is the midpoint of the line segment joining A(-3,b) and B(1, b+4), then the value of b is
a) 1 b) -1 c) 2 d) 0
10) The nth term of an AP is Tₙ= 4n -1. The common difference of the AP is:
a) 2 b) 3 c) -3 d) 4
Day- 20(29/7/24)
1) The shadow of a flag post 25m high is 25√3m. Find the angle of elevation of the Sun. 30°
2) A conical tent has a circular base of area 0.375 hectares . If its height is 20m, find its capacity. 2500m³
3) The sum of two radii of two circles is 18.5cm and the difference of their circumference of their circymference is 22cm. Find the radius of the bigger circle. 11cm
4) In the given figure, AB || CD and O is the centre of the circle. If angle BED=35°, find angle ACD.
5) The line x - y = 3 divides the join of (3,4) and (8,3) in the ratio m: n. Find the ratio. 2:1
6) If A= 2. 0 & B= 14 0
-3 4 -45 44
Find the values of scalar factors X and y, such that xA²+ yA = B.
7) 4x³-12x²+ ax + b has x-3 is a factor but when it is divided by x + 2 the remainder is - 75. Find a and b. -1,3
8) A's income is Rs140 more than B's and C's income is Rs80 more than D's. If the ratio of A's and C's income is 2:3 and the ratio of B's and D's income is 1:2, find the income of each. 400,260,600,520
9) Three numbers are in continued proportion. Their sum is 38 and the sum of their squares is 532. Find the numbers. 8,12,18 or 18,12,8
10) Mrs Mehta plans to invest Rs8456 in shares . She partly invests in 17% share at Rs140 and the remaining amount in 9% share at Rs112. Her income from the second investment is Rs58 more than the first investment. How much did she invest in shares at Rs112? Rs5376
11) If the loan is returned after one year, a person would have to pay Rs6240 only. If it is returned after 2 years he would have to pay Rs6489.60 with compound interest. Calculate the amount of loan and the rate of interest. 6000, 4%
12) Mrs Bhagat deposits Rs1500 every month for 36 months in a bank and receives Rs65655 at the end of 36 months. Find the rate of simple interest paid by the bank on the recurring deposit. 14%
13) Solve the inequation and represent it on the number line x/2 +3 ≤ x/3 +4 < 4x -7, x ∈ R.
14) Find the values of x and y if the matrix
A= x+ y y & B= 2 & C= 3
2x x- y -1 2 with the relation AB = C. -1,5
15) From the following table, find the frequency distribution and calculate the mean marks:
Marks no of students
less than 8 4
less than 16 10
less than 24 22
less than 32 41
Less than 40 50 23.68
16) Prove sin⁶x + cos⁶x = 1- 3 sin²x + 3sin⁴x.
17) Two spheres of the same metal weight 1 kgf and 7 kgf. The radius of the smaller sphere is 2.5cm. the sphere are melted to form a single big sphere. Find the diameter of big sphere. 10cm
18) Draw a ∆ ABC in which AB= 4.6cm, BC= 5.4cm and angle B= 60°. With centre A, draw a circle of radius 2cm. Draw another circle to touch BC at C and which also touches the given circle externally.
20) If A(3,2), B(-2,4) and C(3,-2) are the vertices of ∆ ABC, find the equation of the line perpendicular to AB and passing through the mid point of BC. 10x - 4y-1= 0
21) The difference between the reciprocals of two consecutive multiples of 3 is 1/468, find the numbers. 36,39
22) A man borrowed a certain sum of money. He can pay Rs242000 after 2 years or pay Rs292820 after 4 years to clear the debt alongwith compound interest. find
a) the rate percent per annum
b) the sum borrowed. 10%, 200000
Day- 19(26/7/24)
1) Find the remainder when x³- 5x²+ 9x - 6 by x-2.
2) Find the remainder when x³- 16x -26 is divided by x+3.
3) Find the remainder when x³+ 54 when divided by x+ 4.
4) If 2x³+ x²- 2x - k has 2x+1 as a factor, find k. Hence Factorize completely.
5) When 2x³+ x²- 2x - k is divided by 2x + 2, the remainder is 0. Find k.
6) if 3x³ + ax²- bx - 30 has x - 3 and 3x+ 5 as factors , find a, b.
7) Factorise completely by using factor theorem: 2x³- x²y - 36xy² - 45y³.
8) Given expression f(x)= x²+ n²x + m, h(x)= x²+ m²x + n and m≠ n, given that both the functions have x + a as a common factor, show that a(m + n)+ 1= 0.
Day -18(22/7/24)
1) A point P divides the join of A(6,-2) and B(-5,8) in the ratio 2:3. Find the coordinanates of P.
2) Find the ratio in a which x-axis divides the join of A(7,2) and B(5,-4). 1:2
3) In what ratio is the line joining the points A(-8,6) and B(10,-4) divided by x-axis.
4) In what ratio is the line joining the points A(-12,9) and B(15,-6) divided by y-axis?
5) The midpoint of the line joining A(a,2) and B(3,6) is (2,b). Find the value of a and b.
6) ABCD is a parallelogram. The coordinates of the vertices are A(-4,-2), B(3,-2), C(x,4) and D(-1,2). Find the coordinates of the point C .
7) Find the coordinates of the points A and B where the line 5x + y=10 cuts the x-axis and y-axis respectively. Hence , find the coordinates of the midpoint of AB.
Day- 17(21/7/24)
1) A is the solution set of 8x - 11 > 4x- 3 and B is the solution set of 6x - 2≤ 4x + 10 where x∈ N. Find the set A ∩ B. Hence, graph the solution set on the number line.
2) List the element of the solution set of the following equation: -3< x -2≤ 9 - 3x; x∈R.
3) Solve the inequation |2x - 9|< 6, x ∈Z. State the solution set.
4) List solution set of the inequation; 1/2 + 8x > 5x -3/2, x ∈Z.
5) Find the range of the values of x which satisfy -1/3 ≤ x/2 - 4/3 < 1/6, x ∈ R.
Graph these values of x on the real number line.
6) if - 2≤ 1/2 - 2x/3≤ 11 / 6, x ∈N, then find the solution set and graph it on the number line.
7) Write open mathematical sentences using x for the variables, whose graphs are given below :
Day-16(19/7/24)
1) Solve: √(3x²+ x+5}= x - 3. -4,1/2
2) Roots of the quadric equation are 1/2 and -14. Find the equation. 2x²+ 27x -14= 0
3) 8(t²+ 1/t²)- 42(t - 1/t)+ 29= 0. Find the possible values of t. 15/4,3/2
4) Solve : x²- 6x -15= 0. Give your answer correct to two decimal places. -1.90, 7,9
5) Solve the following:
a) 6x²- x = 35.
b) x² - 8X - 1280 = 0.
c) 1/(2y -9) = 1/(y -3) + 4/5.
d) 2x²+ 11x -10 = 0. Give your answer correct to two decimal places.
e) 5ˣ⁺¹ + 5²⁻ˣ =126.
1) A two digit number is such that the product of digits is 12. When 9 is added to the number the digits are interchanged. Find the number.
2) The sides of a right angle triangle are x cm, 4(x + 1)cm, and (4 x + 5)cm. Find x.
3) A man purchased sheep for Rs4500. Three sheep were lost and the rest he sold for Rs30 more per sheep than he had paid. if his gain on the whole transaction is 8%, how many sheep did he buy ?
4) The sum of the ages of a man and his son is 46 years and the product of their ages is 168 years. Find the age of the son.
5) The total surface area of a cylinder is 75.24 cm² and its height is 3.6 cm. if its radius is x cm, find x.
6) The bill of a party for a certain number of people is Rs19200. If there were 10 more persons, the bill each person had to pay would have reduced by Rs160. Find the number of people at the party. 30
Day-15(15/7/24)
1) A coin is tossed once, what is the probability of getting
a) a head. 1/2
b) a tail. 1/2
c) Both head and tail turn up. 0
d) neither head nor tail turns up. 0
2) A coin is tossed twice, find the probability of getting
a) no head. 1/4
b) both tails . 1/4
3) When two coins toss simultaneously, what possible outcomes. Find the probability of getting
a) both heads. 1/4
b) at least one head. 3/4
c) atleast one tail. 3/4
d) head turns up exactly once. 1/2
e) Tails turns up atleast once. 3/4
f) Tail does not turn up at all. 1/4
g) two heads. 1/4
h) one head. 1/2
i) One tail. 1/2
j) at most one head. 3/4
k) No head. 1/4
4) If 3 identical coins are tossed. What is the probability of getting:
a) all three heads. 1/8
b) one head and two tails. 3/8
c) all three tails. 1/8
d) atleast two head. 1/2
e) all heads. 1/8
f) two heads . 3/8
g) one head. 3/8
h) exactly 2 heads. 3/8
i) atleast 1 head & 1 tail. 6/8
j) atleast 1 head. 7/8
5) A coin is tossed thrice. Find the probability that:
a) Tail turns up atleast twice. 1/2
b) Head does not turn up at all. 1/8
c) Tail comes on the second toss. 1/2
d) Head turns up atleast once. 7/8
e) getting two or more heads. 1/2
f) the second is not a head. 1/2
Day -14(12/7/24)
TAX AND SERVICES TAX
Multiple Choice Questi
ons
1) IGST is charged on:
a) interstate transaction b) intrastate transaction c) both a, b d) none
2) GST payable is equals to
a) ITC --output GST b) output GST + ITC c) output GST - ITC d) output GST
3) A dealer in Mumbai sold a washing machine to a consumer in Mumbai for Rs18000. If the rate of GST is 18% and GST, then SGST is:
a) Rs1620 b) Rs3240 c) nil d) none
4) In a transaction from Delhi to Lucknow, MRP = Rs10000, discount= 10%, GST= 28%. Here IGST is:
a) Rs2520 b) Rs5040 c) nil d) none
5) A refrigerator was sold for Rs15000 under intrastate transaction from station A to station B and the GST rate is 18%. CGST is:
a) Rs1450 b) Rs 1350 c) Rs1300 d) Rs2700
6) A dealer purchased goods worth Rs 15000 and sold them for Rs21000 within the state. If the rate of GST is 12%, then the net SGST paid by the dealer is:
a) Rs360 b) Rs720 c) Rs800 d) Rs850
7) A dealer in Delhi sold a water heater whose marked is Rs22000 to a customer in Delhi at discount of 25%. If the rate of GST 18%, then the SGST paid is:
a) Rs 1485 b) Rs2970 c) Rs1980 d) nil
8) Anushka bought 400g of almonds at Rs1200 per kg. If the rate of GST is 5%, the amount paid by Anushka is:
a) Rs504 b) Rs480 c) Rs1260 d) Rs630
9) A dealer in Agra sold an LED to a customer in Agra for Rs28000. If SGST is Rs2420, then the rate of GST is:
a) 12% b) 18% c) 9% d)28%
10) Mr. Sharma purchased goods worth Rs40000 from a dealer(within the same state ). If the rate of GST 18%, then CGST is:
a) Rs 3600 b) Rs7200 c) Rs8000 d) nil
11) The tax invoice of a mobile company in Delhi shows cost of services provided by it as Rs1200. If the rate of GST is 18%, then amount of the bill is:
a) Rs 1400 b) Rs1308 c) Rs 1416 d) Rs1500
12) A shopkeeper in Rampur sold an oven to a customer in Rampur for Rs26400. If the rate of GST is 28%, then IGST is:
a) Rs3696 b) Rs7392 c) Rs1848 d) nil
13) A dealer in Bhopal (MP) supplies goods worth Rs 30000 to a dealer in Delhi. The dealer in Delhi supplies the same goods to a customer in Delhi at a profit of Rs5000. If the rate of GST is 18%, then the net GST paid by the dealer in Delhi is:
a) Rs900 b) Rs2700 c) Rs5400 d) nil
14) A dealer in Patna (Bihar) supplies goods worth Rs 15000 to a dealer in Sonepat(Haryana). The dealer in Sonepat supplies the same goods to a dealer in Rohtak (Haryana) at a profit of Rs 3000. If the rate of GST is 18%, then the net GST paid by the dealer in Sonepat is:
a)Rs 540 b) Rs700 c) Rs720 d) nil
15) A retailer purchases an iron for Rs1500 from a dealer and sells it to a consumer at 10% profit. If the sales and intrastate , and the rate of GST is 12%, then the selling price of the iron including GST by the retailer is:
a)!Rs1550 b) Rs1848 c) Rs1950 d) Rs
16) A shopkeeper purchased a fan for Rs1500 from a dealer and sold it to a customer at 10% profit. If the sells are intrastate and the rate of GST is 12%, then the tax (under GST) received by the central government is :
a) Rs18 b) Rs99 c) Rs198 d) nil
17) Goods from Delhi are sold to Ranchi(Jharkhand) for Rs20000 and then from Ranchi to Cuttack (Odisha). If the rate of GST is 18%, and the profit made at Ranchi is Rs5000, then the net GST payable by the dealer in Ranchi is :
a) Rs1000 b) Rs900 c) Rs850 d) Rs875
18) A shopkeeper bought an article from a dealer at Rs1000. He sold it to the customer at Rs1200. If the rate of GST is 12%, then the amount paid by the customer to buy the item is:
a) Rs 1200 b) Rs1300 c) Rs1344 d) Rs1350
19) Three friends A, B and C live in Delhi. A sales medicine worth Rs50000 to B, B sells the same medicine to C at a profit of Rs 6000. If the rate of GST is 12%, then SGST paid by B is:
a) Rs300 b) Rs360 c) Rs400 d) Rs425
20) Mr Gupta wanted to book a semidelux room in a hotel for Rs750. Since semidelux room was not available, he booked a delux room for Rs1400. If GST for a room below Rs1000 is 18% and GST for a room above Rs1000 is 28%, then the extra GST paid by Mr Gupta for the delux room is:
a) Rs 257 b) Rs280 c) Rs300 d) Rs425
Short Answer Type Questions:
1) Find the amount of bill for the following intrastate transaction of goods , if the GST rate is 28%.
items I II III
Marked price(Rs) 7000 14700 28200
discount% 20 10 10
2) A registered garment house in Ludhiana (Punjab) sold three lots of garments to a dealer in Bhatinda (Punjab) for Rs1000000; Rs600000 and Rs500000. It also charged Rs10000 on each lot of transportation charges . But on the occasion of Diwali , a discount of 1% was given on each lot . If the rate of GST is 5%, Calculate
a) IGST
b) CGST
c) SGST
3) Saurav went to watch a new movie in a multiplex. He wanted to buy a movie ticket for Rs80, but it was not available. So, he bought a ticket for Rs120. If the GST for a ticket below Rs100 is 18%, and GST for a ticket above Rs100 is 28%, how much extra GST and extra amount did saurav pay for the ticket?
4) A dealer in Rohtak (Haryana) bought a gold ring from a manufacturer in Gurgaon (Haryana) for Rs800000. He sold this ring to a dealer to Nainital (Uttarakhand) for Rs95000. If the rate of GST is 3% find
a) the new GST payable at Rohtak
b) Input tax credit (ITC) for dealer in Nainital.
5) A retailer in Jaipur( Rajasthan) buys goods from a dealer in Alwar (Rajasthan) at a discount 20%. The retailer sales it to a customer in Jaipur at the printed price. If the printed price of the goods is Rs16000 and the GST rate is 8%, calculate :
a) the prince paid by the customer for the goods.
b) the CGST and SGST payable by the retailer in Jaipur to the government.
LONG ANSWER TYPE QUESTIONS
1) An e-learning company in Delhi sets the marked price of an e-book as Rs75000. It sells the e-book to a dealer in Patna (Bihar) at discount of 30%. The dealer in Patna raises the marked price of the e-book by 30% and then sells it to a dealer in Ranchi (Jharkhand). if the rate of GST is 5%, find the GST paid by the dealer in Patna to the government.
2) A manufacturer in Noida (UP) sold a cartoon of hair oil to a dealer in Rajpur (Chhattisgarh) for Rs22000. The dealer in Raipur sold it to a consumer in Bastar (Chhattisgarh) at a profit of Rs5000. If the rate of GST is 18%, find:
a) the net IGST , CGST and SGST payable by the dealer in Raipur.
b) the cost price of the hair oil for the customer.
3) A dealer in Jodhpur (Rajasthan) supplied floor tiles worth Rs1700000 to a dealer in Delhi and another worth Rs300000 to a dealer in Jaipur (Rajasthan). The total value of his receipt of tiles in interstate transactions was Rs1500000. If the rate of GST is 18%, calculate the net IGST , CGST and SGST payable by the dealer in Jodhpur.
4) A shopkeeper sells an item for Rs2150. For a customer, he reduced the price of the item in such a way that the customer has to pay only Rs2124 including GST. If the rate of GST is 18%. Calculate the amount of reduction allowed by the shopkeeper .
5) A fruit juice company in Allahabad (UP) sold fruit juice worth Rs16000 to a dealer in Hapur(UP). The whole lot of juice was then supplied to a dealer in Rudrapur (Uttarakhand) for Rs17500. If the rate of GST is 12%. Find :
a) the net GST payable at Hapur.
b) input Tax credit (ITC) for the dealer in Rudrapur.
6) Radheshyam is a dealer of footwear in Moradabad (UP). He purchase footwear worth Rs200000. He sold 50% of thess footwear to a dealer in Agra (UP) for Rs130000 and the rest of the stock remains in his godown. If the rate of GST is 5%, find the excess credit of CGST and SGST to be carried forward.
7) The marked price of a video camera Recording is Rs80000. A dealer in Delhi buys it from a dealer in Mumbai (Maharashtra) at discount of 20% on the marked price . The dealer then sells it to a customer in Rohtak (Haryana) at a discount of 10% on the marked price. if the rate of GST is 18%, calculate the amount of tax payable by the dealer in Delhi to the government
Day13(17/6/24)
1) Yash opens a recurring deposit account with the bank of Rajasthan and deposits ₹600 per month for 20 months. Calculate the maturity value of this account, if the bank pays intrest at the rate of 10% per month. 13050
2) A recurring deposit account of ₹1200 per month has a maturity value of ₹12440. If the rate of interest is 8% and the intrest is calculated at the end of every month, find the time of this recurring deposit account. 10 months
3) Sujata deposited, a certain sum of money, every month, for 2 and half years (5/2 yrs) in a cumulative time deposit account. At the time of maturity she collected ₹4965. If the rate of interest was 8% p.a. find the monthly deposit. 150
4) Sumit paid ₹300 per month in a cumulative time deposit account for 2 yrs. He received ₹7875 as the maturity amount. Find the rate of interest. 9%
5) On depositing ₹200, every month in a cumulative time deposit account, paying 9% p.a. intrest, a person collected ₹117 as intrest. Find the period. 12 months
1) Find the range of values of x, which satisfy the inequality -1/5 ≤ 3x/10 +1 < 2/5, x belongs to R. Graph the solution set on the number line. 4≤x <-2
2) Solve the following inequation, and graph the solution set on the number line: 2y - 3 < y+ 2 ≤ 3y+ 5, y(-R). The solution set={y: y belongs to R, -3/2 ≤ y < 5}
3) 5x/4 - (4x -1)/3 > 1, x belongs to R. Show in number line. {x:x<-8, x belongs to R}
4) 2x -1 ≥ x + (7- x)/3 > 2.
5) If P is the solution set of -3x +4< 2x -3, x belongs to N, Q is the solution set of 4x -5 < 12, x belongs to W, find
A) P ∩ Q
B) P - Q
C) P' ∩ Q
1) (x-3)/(x+3) + (x+3)/(x-3) = 5/2, x≠- 3, x ≠ 3. -9,9
2) 2x -3 =√(2x² - 2x +21). 6
3) a/(ax -1) + b/(bx -1)= a+ b, a+ b≠ 0, ab≠ 0. (a+ b)/ab, 2/(a+ b)
4) 2x²- 9x +10= 0, when
A) x belongs to N. 2
B) x belongs to Q . 2, 5/2
5) 3x²- x - 7 correct upto two decimal places. 1.70 or -1.37
6) 2/(x -1) + 3/(x+1) = 4/(x+2). Correct to 2 significant figures. 0.23 or -8.77
7) A train covers a distance of 600 km at x km/hr. Had the speed been (x+20) km/hr, the time taken to cover the distance would have been reduced by 5 hours. Write down an equation in terms of x and solve it to evaluate x. 40
8) The cost of 2x articles is ₹(5x+54) while the cost of (x +2) articles is ₹ (10x -4). Find x. 6
9) The difference of the square of two numbers is 45. The square of the smaller number is 4 times the larger number. Determine the numbers. 9,6
10) A year ago the father was 8 times as old his son. Now his age is the square of his son's age. Find their present ages. 49,7 yrs
11) The length of the hypotenuse of a right angled triangle exceeds the length of the base by 2cm and exceeds twice the length of the altitude by 1 cm. Find the length of each side of the triangle. 8, 15,27
12) The sum of the numerator and denominator of a fraction is 8. If 1 is added to both the numerator and denominator, the fraction is increased by 1/15. Find the fraction. 3/5
1) A: B =1/4 : 1/5 and B : C = 1/7: 1/6, find A: B: C. 15:12:14
2) Find the number which bears the same ratio to 7/33 that 8/21 does to 4/9. 2/11
3) A bag contains ₹142 in the form of one-rupee, 50-paise and 20-paise coins in the ratio 3:5:8. Find the number of coins of each type. 60,100,160
1) Find the remainder when 3x³+ 5x²-11x -4 is divided by 3x+1. 1/9
2) Find the values of a and b, if x-2 and x+3 are both factors of x³+ ax²+ bx - 12. 3,-4
3) Find the value of a if the division of x³+ 5x²- ax +6 is divided by x-1 leaves the remainder 2a. 4
4) If 3x -2 is the factor of 3x³ - kx² +21x - 10, then find k. 11
5) Prove that x- 5 is a factor of 2x²- x -45. Hence, factorise completely. (x-5)(2x+9)
6) y³ - 13y -12 factorise completely. (y+1)(y-4)(y+3)
1) a -2 = 2 c
b 7 3 2c+ d then find a,b,c,d. 2,3,-2, 11
2) If A= 3 -4 & B= 0 2
0 1 3 -1 find the Matrix X if 2A + 3X = 5B.
3) If A= 1 2 B= -2 -1 C= 0 3
-2 3 1 2 2 -1 find A+ 2B - 3C.
4) If x+ 3y = 1 2 and 2x + y= 5 0
-1 5 -3 3 find the Matrix x and y.
5) If A= 1 1
8 3 evaluate A² - 4A.
6) If X= 4 1
-1 2 show that 6X - X² = 9I, where I is unit Matrix.
7) If B= 4 -5 & C= 10 -11
-2 1 12 -15 find the Matrix A such that AB= C.
1) The point P(3,4) is reflected to P' in the x-axis and O' is the image of O(origin) when reflected in the line PP'. Using graph paper, give:
A) The coordinates of P' and O'
B) The length of the segment PP' and OO'.
C) The perimeter of the quadrilateral POP'Q'.
D) The geometrical name of the figure POP'Q'. (-3,4), 6, 20, Rhombus
2) Use a graph paper for this question. Plot the points P(3,2) and Q(-3,-2). From P and Q, draw perpendiculars PM and QN on the x-axis.
A) name the image of P on reflection in the origin.
B) Assign the special name to the geometrical figure PMQN and find its area.
C) Write the coordinates of the point to which M is mapped on reflection in (i) x-axis (ii) y-axis (iii) origin. Q, parallelogram, 18, (3,0),(-3,0),(-3,0)
3) A point P is reflected in the origin. Coordinates of its image are (2,-5). Find
A) the coordinates of P. (-2,5)
B) the coordinates of the image of P in the x-axis. (-2,-5)
4) The point A(2,3), B(4,5) and C(7,2) are the vertices of ∆ABC.
A) Write down the coordinates of A', B', C' if ∆A'B'C', is the image of ∆ABC when reflected in the origin. (-2,-3),(-4,-5),(-7,-2)
B) Write down the coordinates of A", B", C" if A"B"C" is the image of ∆ABC when reflected in the x-axis. (2,-3),(4,-5),(7,-2)
C) Assign the special name to the quadrilateral BCC"B" and find its area. Isosceles trapezium, 33 sq units
5) A) point P(a,b) is reflected in the x-axis to P'(5,-2). Write down the values of a, b. 5,2
B) P" is the image of P when reflected in the y-axis. Write down the coordinates of P". (-5,2)
C) Name a single transformation that maps P' to P". Reflection in the origin
1) Find the coordinates of the point C which divides the join of A(4,-3) and B(9,7) in the ratio 3:2. (7,3)
2) Find a point P on the line segment joining A(14,-5) and B(-4,4), which is twice as far from A as from B. (2,1)
3) The midpoint of the line joining (a,2) and (3,6) is (2,b). Find a, b. 1,4
4) The midpoint of the line joining (2a,4) and (-2,3b) is (1, 2a+1). Find a, b. 2,2
5) The line segment joining A(2,3) and B(6,-5) is intersected by x-axis at a point k. Write down the ordinate of the point k. Hence, find the ratio in which k divides AB. 0, 3:5
6) Calculate the ratio in which the line segment joining (3,4) and (-2,1) is divided by the y-axis. 3:2
7) Find the coordinates of the vertices of the triangle, the middle point of whose sides are (0,1/2), (1/2,1/2),(1/2,0). (0,0),(1,0),(0,1)
8) If (0,b),(-a/2, b/2),(a/2, b/2) are the midpoints of the sides of a triangle, find the coordinates of its centroid. (0,2b/3)
1) Find the value of p, given that the line y/2 = x - p passes through the point (-4,4). -6
2) The equation of the line PQ is 3y - 3x +7= 0.
A) find the slope of PQ. 1
B) calculate the angle that the line PQ makes with the positive direction of x-axis. 45°
3) The graph of the equation y= mx + c passes through the points (1,4) and (-2,-5). Find the value of m and c. 3,1
4) Find the equation of the line passing through the point (2,-5) and making an intercept of -3 on the y-axis. x+y+3= 0
5) Find the equation of a straight line passing through (-1,2) and slope is 2/5. 2x- 5y+ 12= 0
6) Find the equation of a straight line passing through the origin and through the point of intersection the lines 5x+ 7y -3= 0 and 2x - y= 7. x+2y= 0
7) Calculated the coordinates of the point of intersection of the lines by x+y -6= 0 and 3x - y = 2. (2,4)
8) The vertices of a triangle ABC are A(2,-11), B(2,13) and C(-12,1). Find the equation of its sides. x-2= 0, 6x - 7y+ 79= 0, 6x+ 7y+ 65= 0
9)A(2,-4) B(3,3) and C (-1,5) are the vertices of a ∆ ABC . Find the equation of the median of the triangle through A. 8x+y -12= 0
1) A girl fills a cylindrical bucket 32cm in height and 18 cm in radius with sand. She emptied the bucket on the ground and makes a conical heap of the sand. If the height of the conical heap is 24cm.
A) find its radius. 36cm
B) its slant height. √1872
( leave your answer in square root from)
2) Water flows at the rate of 10 m per minute through a cylindrical by 5 mm in diameter. How long would it take to fill a conical vessel whose diameter at the base is 40 cm and depth 24 cm ? 51min 12sec
3) An exhibition tent is in the form of the cylinder surmounted by a cone. The height of the tent above the ground is 85 m and the height of the cylindrical part is 50m. If the diameter of the base is 168m, find the quantity of canvas required to make the tent. Allows 20% extra foe folds and for stitching, give your answer to the nearest m². 60509 m²
4) From a solid cylinder whose height is 8 cm and radius 6cm, a conical cavity of height 8 cm and base radius 6 cm is hollowed out. Find the volume of the remaining solid correct to 4 significant figures also find the total surface area of the remaining solid spherical metallic solid. 603.2, 603.2
5) A spherical metallic ball of radius 3 cm is melted and recast into three spherical balls. The radii of 2 of these balls are 2.5 cm and 2 cm respectively. Find the radius of third ball. 1.5cm
6) A cylindrical can whose base is horizontal and of radius 3.5cm contains sufficient water so that when a sphere is placed in the can, the water just covers the sphere. Given that the sphere just fits into the can. calculate
A) the total surface area of the can in contact with water when the sphere is in it. 385/2
B) the depth of water in the can before the sphere was put into the can take π to be 22/7. 7/2
7) the internal and external radii of a hollow sphere are 3cm and 5 cm respectively. the sphere is melted to form a solid cylinder of 8/3 cm. Find the diameter and curved surface area of the cylinder. 14, 352/3
1) (cos³x + sin³x)/(cosx + sinx) + (cos³x - sin³x)/(cosx- sinx)
2) cosx/(1- tanx) + sinx/(1- cotx)
3) sinx/(cotx + cosecx) = 2+ sinx/(cotx - cosecx)
4) √{1+ cosx)/(1- cosx)}= cosecx + cotx
5) 1/(sinx + cosx) + 1/(sinx - cosx) = 2 sinx/(1- 2 cos²x)
6) sec²x + cosec²x = sec²x cosec²x.
7) sin⁴x + sin²x cos²x = sin²x
8) sin⁴x cosec²x + cos⁴x sec²x =1
9) tan⁴x + tan²x = sec⁴x - sec²x.
10) sin²x/(sinx - cosx) + cosx/(1- tanx) = sinx + cosx.
11) sin⁶x + cos⁶x = 1- 3 sin²x cos²x.
1) Construct a histogram for the following frequency distribution.
Class-interval frequency
05-12 4
13-20 12
21-28 26
29-36 15
37-44 6
45-52 18
2) Draw an Ogive for the following distribution.
Marks. no of students
00-10 6
10-20 9
20-30 11
30-40 23
40-50 28
50-60 32
60-70 21
70-80 14
80-90 4
90-100 2
3) Draw a more than cumulative frequency curve for the following data:
Class-interval frequency
00-10 4
10-20 5
20-30 11
30-40 14
40-50 11
50-60 10
60-70 6
4) If 7 is the mean of 5, 3, 0.5, 4.5, b, 8.5, 9.5. find b. 18
5) Find the mean of following distribution:
Class-interval frequency
00-50 4
50-100 8
100-150 16
150-200 13
200-250 6
250-300 3 143
6) Given below are the weekly wages of 200 workers in a small factory:
Weekly wages no of workers
80-100 20
100-120 30
120-140 20
140-160 40
160-180 90
Calculate the mean weekly wages of the workers. 145
7) Calculate the mean, the median and the mode of the following:
3,1,5,6,3,4,5,3,7,2. 3.9,3.5,3
8) The marks scored by 19 students in a test are given below:
31,22,36,27,25,26,33,24,37,32,29,28,36, 27,35,35,32,26,28. Find
A) median. 29
B) lower quartile. 26
C) upper quartile. 35
D) inter quartile. 9
9) From the following frequency distribution, find median , lower quartile, upper quartile, semi-inter- quartile
Variate: 13 15 18 20 22 24 25
Frequ: 6 4 11 9 16 12 2
21,18,22,2
10) Marks obtained by 120 students in a Mathematics test are given below:
Marks. No of students
00-10 5
10-20 9
20-30 16
30-40 22
40-50 26
50-60 18
60-70 11
70-80 6
80-90 4
90-100 3
Draw the Ogive for the given distribution. Use a suitable scale for your Ogive. Use your Ogive to estimate
A) the median. 43.5
B) the lower quartile. 30
C) the number of students who obtained more than 75% in the test. 10
D) the number of students who did not pass in the test if the pass percentage was 40. 52
11) The daily profits in rupees of 100 shops in a departmental store are distributed as follows:
Profit per shop(in ₹) no of shops
000-100 12
100-200 18
200-300 27
300-400 20
400-500 17
500-600 6
Draw a histogram of the above data on a graph paper and hence estimate the mode. 255
Day 12(14/6/24)
1) Which one of the following is a polynomial?
a) f(x)= x + 1/x b) g(x)= (x-1)(x-3)/x c) h(x)= (x + 2)/(x+1) d) p(x)= 2x² + (5x³⁾²+ 4√x)/√x
2) √3 is a polynomial of degree
a) 2 b) 0 c) 1 d) 1/2
3) Which of the following is a polynomial?
a) x²+ 2x⁻¹+3 b) x + x⁻¹+5 c) 2x⁻¹ d) 0
4) If x¹⁰¹ + 101 is divided by x+1, then the remainder is
a) 0 b) 100 c) 101 d) 1
5) If f(x)= x¹⁰⁰+ 2x⁹⁹ + k is divisible by (x +1), then the value of k is
a) 1 b) 2 c) -2 d) -3
6) The remainder when f(x)=x³- 2x²+ 6x -2 is divided by (x -2) is
a) 5 b) 8 c) -10 d) 10
7) The remainder when f(x)=x³+ ax²+ 6x + a is divided by (x + a), is
a) -5a b) 5a c) 10a d) 0
8) If (x - a) is a factor of the polynomial p(x)= x³- ax²+ 2x + a - 6, then the value of a is
a) 1 b) -1 c) 2 d) -2
9) If f(x+3)= x²- 7x +2, then the remainder when f(x) is divided by (x +1) is
a) 8 b) -4 c) 20 d) 46
10) If f(x + 1/x)= x²+ 1/x², the remainder when f(x) is divided by x-3 is
a) 10 b) 11 c) 7 d) 5
11) If f(x+1)= 2x²+ 7x +5, then one of the factors of f(x) is
a) 2x+3 b) 3x+2 c) 2x -3 d) 3x -2
12) If (x -2) is a factor of f(x)= x²+ ax +1, then the remainder when x²+ ax +1 is divided by (2x +3) is
a) 7 b) 8 c) 1 d) 0
13) If (x -3) is a factor of f(x)=x²+ a, then the remainder when f(x) is divided by (x -2) is
a) 5 b) -5 c) 13 d) -13
14) if (2x -1) is a factor of f(x)=2x²+ ax -2, then the other factor of f(x) is
a) x -2 b) x+2 c) x -1 d) x+1
15) if (x +1) and (x -1) are factors of f(x)= ax³+ bx²+ cx + d, then
a) a+ b= 0 b) b + c= 0 c) b+ d= 0 d) a+ d= 0
16) when the polynomials p(x)=ax² + bx +c is divided by (x- 1) and (x + 1), the remainders obtained are 6 and 10 respectively. If the value of p(x) at x= 0 is 5, then 5a - 2b + 5c=
a) 21 b) 40 c) 42 d) 44
17) if f(x+3)=x² + x-6, then one of the factor of f(x) is
a) x - 3 b) x -4 c) x - 5 d) x - 6
18) The ratio of the remainders when f(x)= x² + ax + b is divided by (x - 2) and (x- 1) respectively is 4:3. If (x -1) is a factor of f(x), then
a) a=9, b= - 10 b) a= - 9, b= 10 c) a=9, b= 10 d) a=-9, b= -10
19) If a quadratic polynomial f(x) leaves remainder 4, 4 and 0 respectively when divided by (x -1) and (X - 3) respectively then f(x)=
a) -2x² +6x+ 3 b) -2x²+6x c) -2x² + 6x +5 d) -2x²+6x -5
20) The remainder when f(x)= x⁵ is divided by g(x)=x² -9, is
a) 81x b) 81x + 10 c) 243x + 81 d) 0
21) Which one of the following is a polynomial ?
a) x²/2 - 2/x² b) √(2x) - 1 c) x²+ 3x³⁾²/√x d) (x -1)/(x+ 1)
22) Degree of the zero polynomial is
a) 0 b) 1 any natural number d) not defined
23) √2 is a polynomial of degree
a) 2 b) 0 c) 1 d) 1/2
24) Zero of the zero polynomial is
a) 0 b) 1 c) any real number d) not defined
25) if f(x)= x + 3 then f(x) - f(x) is equals to
a) 3 b) 2x c) 0 d) 6
26) Zero the polynomial f(x)= 3x + 7
a) 7/3 b) -3/7 c) 7/3 d) -7
27) One of the zeros of the polynomials f(x)= 2x² + 7 x - 4 is
a) 2 b) 1/2 c) -1/2 d) -2
28) If f(x)= x²- 2√2x+ 1, then f(2√2) is equals to
a) 0 b) 1 c) 4√2 d) 8√2 + 1
29) x + 1 is a factor of the p
olynomial
a) x³ + x² - x + 1 b) x³+ x² + x + 1 c) x⁴ + x³ + x² + 1 d) x⁴+ 3x³+ 3x² + x +1
30) If x²+ kx + 6 = (x+ 2)(x + 3) for all, then the value of k is
a) 1 b) -1 c) 5 d) 3
31) If x - 2 is a factor of the x²+3ax -2a, then a=
a) 2 b) -2 c) 1 d) - 1
32) If x³+ 6x² + 4 x + k is exactly divisible by x + 2, then k=
a) -6 b) - 7 c) - 8 d) - 10
33) If x - a is a factor of x³- 3xa²+ 2a²x + b, then the value of b is
a) 0 b) 2 c) 1 d) 3
34) If x¹⁴⁰ + 2x¹⁵¹ + k is divisible by x + 1, then the value of k is
a) 1 b) -3 c) 2 d) - 2
35) If x + 2 is a factor of x² + mx + 14, then m=
a) 7 b) 2 c) 9 d) 14
36) If x - 3 is a factor of x² - ax - 15, then a=
a) - 2 b) 5 c) - 5 d) 3
37) If x⁵¹+ 51 is divided by x + 1, the remainder is
a) 0 b) 1 c) 49 d) 50
38) if x+ 1 is a factor of the polynomial 2x² + kx, then k=
a) - 2 b) - 3 c) 4 d) 2
39) If x + a is a factor of x⁴ - a²x² + 3 x - 6a, then a =
a) 0 b) - 1 c) 1 d) 2
40) The value of k for which x -1 is a factor of 4 x³ + 3x²- 4x + k, is
a) 3 b) 1 c) -2 d) -3
41) if x+ 2 and x-1 are factors of x³+ 10x²+ mx + n, then the value of m and n are respectively
a) 5 and - 3 b) 17 and -8 c) 7 and 18 d) 23 and -19
42) let f(x) be a polynomial such that f(-1/2)= 0, then a factor of f(x) is
a) 2x - 1 b) 2x + 1 c) x -1 d) x + 1
43) When x³ - 2x² + ax - b is divided by x² - 2x - 3, the reminder is x -6. The values of a and b are respectively
a) -2, - 6 b) 2 and -6 c) - 2 and 6 d) 2 and 6
44) One factor of x⁴+ x²- 20 is x² +5. The other factor is
a) x²-4 b) x -4 c) x²-5 d) x +4
45) if x -1 is a factor of polynomial f(x) but not of g(x), than it must be a factor of
a) f(x) + g(x) b) -f(x) + g(x) c) f(x) - g(x) d) {f(x) + g(x)}g(x)
46) (x+ 1) is a factor of xⁿ +1 only if
a) n is an odd integer b) n is an even integer c) n is a negative integer d) n is a positive integer
47) If x² + x + 1 is a factor of the polynomial 3x³ + 8 x² + 8 x + 3 + 5k, then the value of k is
a) 0 b) 2/5 c) 5/2 d) - 1
48) If (3x -1)⁷= a₇x⁷ + a₆x⁶ + a₅x⁵ ....a₁x + a₀, then a₇ + a₆ + a₅ + ....a₁ + a₀ =
a) 0 b) 1 c) 128 d) 64
49) If both x - 2 and x - 1/2 are factors of px² +5 x + r, then
a) p= r b) p+ r= 0 c) 2p + r= 0 d) p+ 2r = 0
50) if x²-1 is a factor of ax⁴ + bx³ + cx² + dx + e, then
a) a + c+e= b + d b) a + b +e= c+ d c) a + b + c = d + e d) b+ c+ d = a+ e
51) If f(x +3) = x² - 7x + 2, then the reminder when f(x) is divided by x + 1 is
a) 8 b) - 4 c) 20 d) 46
52) If f(x + 1/x) = x² + 1/x², then the remainder when f(x) is divided by (2x+ 1), is
a) -7/4 b) -9/4 c) 9/4 d) 11/4
53) If f(x - 1/x) = x² + 1/x², then the remainder when f(x) is divided by x - 3, is
a) 10 b) 11 c) 7 d) 82/9
54) If f(x -2) = 2x²- 3x +4, then the reminder when f(x) is divided by x - 1, is
a) 3 b) 9 c) 13 d) -13
55) When the polynomial p(x)= ax² + bx + c is divided by x, x - 2 and x + 3, the remainders obtain are 7, 9 and 49 respectively. The value of 3a + 5 b + 2c is
a) - 5 b) 5 c) 2 d) - 2
56) if (x-a) and (x - b) are factors of x² + ax + b, then
a) a=1, b=-2 b) a =-2, b=1 c) a = - 2, b= -3 d) a= -1/3, b= -2/3
57) If (x -a) and (x - b) are factors of x²+ ax - b, then
a) a=-1, b=-2 b) a =0, b=1 c) a = - 1/2, b= 1/2 d) a= -1, b= 2
58) The ratio of the remainders when f(x)= x²+ ax + b is divided by (x -2) and (x- 3) respectively is 5:4. If (x -1) is a factor of f(x), then
a) a= -11/3, b=14/3 b) a =-14/3, b=11/3 c) a = 14/3, b= -11/3 d) a= -14/3, b= -11/3
59) The remainder when f(x)= x⁴⁵ + x²⁵+ x¹⁴+ x⁹+ x is divided by g(x)= x²- 1 is
a) 4x -1 b) 4x +2 c) 4x +1 d) 4x -2
ASSERTION - REASON
Each of the following examples contains STATEMENT-1(Assertion ) and STATEMENT-2 (Reason) and has falling for choices (a), (b), (c) and (d), only one of which is the correct answer. Mark the correct choice.
a) Statement p-1 and Statement-2 are true; Statement -2 is a correct explanation for statement-1.
b) Statement -1 and Statement -2 are true; Statement-2 is not correct explanation for statement-1 .
c) Statement -1 is True , Statement -2 is False
d) Statement -1 is false, Statement -2 is true.
1) Statement -1(A): if a≠ 0 and ax²+ bx + a is exactly divisible by (x - a), then a²+ b +1= 0.
statement-2 (R): if (x - a) is a factor of a polynomial f(x), then f(a)= 0. a
2) Statement -1(A): if x+7 is a factor of f(x)= x² + 11x- 2a, then a =-14.
statement-2 (R): if x+ a is a factor of a polynomial, then f(a)= 0. c
3) Statement-1(A): if the polynomial f(x)= 2x³ + 3x² - 5 x + 7a when divided by x+ 2 leaves the remainder 3a + 2, then a = 2.
statement-2 (R): the remainder when a polynomial p(x) is divided by is given by (x - a) is given by p(a). a
4) statement-1(A): if sum of all the coefficients, including the constant term, of polynomial is zero, then (x -1) is one of its factor.
statement-2 (R): if a polynomial f(x) is divided by (x - k), then f(k)= 0. a
5) Statement-1(A): if f(x + 2)= 2x² +x - 3 is divided by (x - 1), the remainder is 2.
statement-2 (R): if f(x) is divided by (2 - 3 0x), the remainder is f(2/3). d
6) statement-1(A): if the polynomial p(x)= x³+ ax²- 2x + a + 4 has (x + a) as one of its factors , then a= 4/3.
statement-2 (R): if f(x)= ax² + b + c is exactly divisible by (2x - 3) then 4a + 6b + 9 = 0. b
7) statement-1(A): If the polynomial f(x)= 3x⁴ - 11 x² + 6x + k when divided by (x - 3) leaves remainder 7, then k =-155.
Statement-2 (R): if a polynomial is divided by (x - a), the reminder is f(a). a
8) statement-1 (A): if f(x+2)= 2x² + 7x + 5, then the reminder when f(x) is divided by (x - 1) is 0.
Statement-2 (R): if a polynomial f(x) is divided by (ax + b), then the remainder is f(b/a). c
9) Statement -1(A): if x + 1 is a factor of f(x)=px² + 5 x + r, then p+ r+ 5 = 0.
Statement -2(R): if x - 2 and 2x - 1 are factors of f(x)= px² + 5 x + r, then p= r. d
10) Statement -1(A): If x + 2a is a factor of f(x)= x⁵- 4a²x³ +2x +2a + 3, then 2a - 3= 0.
Statement -2(R): if f(x) divisible by (ax + b), then f(a/b)= 0.
Day- 11 (12/6/24)
1) If x> 0 and y< 0, the point (x, -y) lies in
a) I quadrant b) II quadrant c) III quadrant d) IV quadrant
2) The points O(0,0), A(4,0) and B (0,4)
a) are collinear b) form a scalene triangle c) form an equilateral triangle d) form an isosceles right triangle
3) if |x|> 0 and y< 0, then the quadrant in which the point representing (x, y) can lie are
a) I, II b) II, III c) III, IV d) IV, I
4) If the coordinates of a point P(x, y) satisfy the relation xy> 0, then Pnmay lie
a) I or II quadrant b) II or III quadrant c) I or III quadrant d) I or IV quadrant
5) The area of the triangle the Co-ordinates of whose vertices are O(0,0), A(6,0) and B (0,8) is
a) 48 sq. units b) 24 sq. unit c) 14 sq. unit d) 12 sq. units
6) The perpendicular distance of the point (-7,4) from y-axis is
a) 7 units b) 4 units c) 11 units d) -7 units
7) The perpendicular distance of the point (3, -4) from x-axis is
a) 3 units b) -4 units c) 4 units d) 7 units
8) The distance of the point P(-6,8) from the origin is
a) 6 units b) 8 units c) 14 units d) 10 units
9) If the point P(x,y) lies in the fourth quadrant, then
a) x> y b) x <y c) x > - y d) y > - x
10) If point P and Q have a coordinates (- 2,7) and (- 5,9) respectively , then the value of (abscissa of P) - (abscissa of Q), is
a) 3 b) - 3 c) - 2 d) 2
11) The reflection of the point P( - 4, 5) in the y-axis has the coordinates
a) (-4, -5) b) (4,5) c) (4, - 5) d) (5, - 4)
12) If points P(3,0) and Q(a,0) are equidistance from the origin, then a=
a) 3 b) - 3 c) 6 d) 9
13) The area of the figure formed by joining the point A(4,4), B( 4,-4), C(-4,-4) and D(-4,4) in order, then the area of the figure formed is
a) 16 square unit b) 32 square units c) 64 square units d) 48 square units
14) The area of the figure formed by joining the points A(-1,5), and (-2,4) and their reflections on y-axis is
a) 3 sq.units b) sq units c) 4 sq units d) 12 sq units
15) The points P(5,-1) on reflection in x-axis is mapped as Q and the point Q on reflection in y-axis is mapped as R, the coordinates of R are
a) (-5,-1) b) (-5,1) c) (5,1) d) (1,5)
16) in question 15, the distance between Q and R is
a) 2 unit b) 6 units c) 5 units d) 10 units
17) The image of a point P under reflection in the x-axis has the coordinates (7,-3). The Co-ordinate of P are
a) (7,3) b) (-7,3) c) (-7,-3) d) (-3,7)
18) The line represented by the equation 8x + 3y = 24 cuts the coordinate axes at A and B. The area of the triangle AOB is
a) 24 square units b) 12 square units c) 48 square units d) 16 square unit
19) The point of intersect of the coordinate axes is
a) ordinate b) abscissa c) quadrant d) origin
20) The abscissa and ordinate of the origins are
a) (0,0) b) (1,0) c) (0,1) d) (1,1)
21) The measure of the angle between the co-ordinate axes is
a) 0° b) 90° c) 180° d) 360°
22) A point whose abscissa and ordinate are 2 and -5 respectively, lies in
a) first quadrant b) second quadrant c) third quadrant d) fourth quadrant
23) Points (-4,0) and (7,0) lie
a) ompn x-axis b) y-axis c) in first quadrant d) in second quadrant
24) The ordinate of any point on x-axis is
a) 0 b) 1 c) -1 d) any number
25) The abscissa of any point on y-axis is
a) 0 b) 1 c) -1 d) any number
26) The abscissa of a point is positive in the
a) first quadrant b) second quadrant c) third quadrant d) fourth quadrant
27) A point whose abscissa is -3 and ordinate 2 lie in
a) first quadrant b) second quadrant c) third quadrant d) fourth quadrant
28) Two points having same abscissa but different ordinates lie on
a) x-axis b) y-axis c) a line parallel to y-axis d) a line parallel to x-axis
29) The perpendicular distance of the point P(4,3) from the x-axis is
a) 4 b) 3 c) 5 d) none
30) The perpendicular distance of the point P(4,3) from the y-axis is
a) 4 b) 3 c) 5 d) none
31) The point (other than origin) for which abscissa is equal to the ordinate will lie in
a) first quadrant only b) I and II quadrants c) I and III and quadrants d) II and IV quadrant
32) Signs of abscissa and ordinate of a point in the second quadrant are respectively
a) +,+ b) -,- c) -,+ d) +,-
33) Abscissa of all points on the x-axis is
a) 0 b) 1 c) 2 d) any number
34) Ordinate of all points on the y-axis is
a) 0 b) 1 c) 2 d) any number
35) A point whose abscissa and ordinate both are negative will lie in
a) lie I quadrant b) lie in II quadrant c) lie in IV quadrant d) do not lie the same quadrant
36) The points whose abscissa and ordinate have different signs will lie in
a) I and II quadrant b) II and III quadrant c) I and III quadrant d) II and IV quadrant
37) Abscissa of a point is positive in
a) I and II quadrant b) I and IV quadrant c) I quadrant only d) II quadrant only
38) On plotting the points O(0,0) A(3,0), B(3,4) C(0,4) and joining OA, AB, BC and CopO which of the following figure is formed?
a) square b) rectangle c) trapezium d) rhombus
39) The image of the point (3,4) in x-axis has the ordinates
a) (-3,4) b) ( 3,-4) c) (-3,-4) d) (4, 3)
40) The image of the point (-5,7) in y-axis has the Co-ordinates
a) (5,7) b) (-5,-7) c) ( 5,-7) d) (7,-5)
41) if the perpendicular distance of a point P from the x-axis is 5 units and the foot of the perpendicular lies on the negative direction of x-axis, then the point P has
a) x ordinanate 5 b) y co-ordinate = 5 only c) y coordinanate=- 5 only d) y coordinanate = 5 or - 5
42) If the mirror image of the point P(5,2) in x-axis is the point Q and the image of Q in y-axis is R. Then, the coordinans of R are
a) (5,-2) b) (-5,-2) c) (- 5,2) d) (2,5)
43) The distance of the point P(4,3) from the origin is
a) 4 b) 3 c) 5 d) 7
44) The area of the triangle formed by the point A(2,0), B(6,0), C(4,6) is
a) 24 square units b) 12 square units c) 10 square units d) none of these
45) The area of the triangle formed by the point P(0,1) Q(0,5), R(3,4) is
a)16 square unit b) 8 sq units c) 4 sq units d) 6 sq units
46) The area of the triangle formed by the point P(-3,4) and its reflection in the Co-ordinates axes is
a) 24 sq units b) 48 sq units c) 16 square unit d) 12 sq units
47) The distance between the reflections of the point P(-3,4) in the coordinate Axes is
a) 8 unit b) 6 unit c) 14 units d) 10 units
48) The quadrilateral formed the by joining the points A(0,0), B(5,0) and C(3,2), D( 0,2) in order is a
a) square b) parallelogram c) trapezium d) rectangle
49) The area of the figure ABCD formed by joining A(-1,1), B(5,1), C( 5,6), D(- 1,6) is
a) 40 square unit b) 30 sq units c) 20 square unit d) 16 square unit
50) The distance between the points (-5,12), and (7,12) is
a) 5 ynits b) 7 units c) 12 units d) 17 units
51) The distance between the images of point P(-7,4) and Q(7,4) in x-axis is
a) 7 units b) 8 units c) 11 units d) 14 units
52) The distance of the point P(-6,8) from the origin is
a) 6 units b) 8 units c) 10 units d) 14 units
53) if the points P(4,2) is translated parallel to x-axis to the 8 units , then the coordinates of new position of P are
a) (4,10) b) (4,6) c) (12,2) d) (4,-6)
CASE STUDY
1) Class IX Students of a school in Moti Nagar, Delhi have been allotted a rectangular plot of land, adjacent to their school, for gardening activity . Sapling of Gulmohar are planted on the boundary at a distance of 1 m from each other. There is a triangular lawn in the plot as shown in figure. The students are to sow seeds of flowering plants on the remaining area of the plot. Considering A as origin, AD along x-axis and AB along y-axis, answer the following questions :
i) The coordinates of A are
a) (0,1) b) (1,0) c) (0,0) d) (- 1,-1)
ii) The coordinates of P are
a) (4,6) b( 6,4) c) ( 4,5) d) (5,4)
iii) The coordinates of R is
a) (6,5) b) (5,6) c) ( 6,0) d) (7,4)
iv) The coordinates of D are
a) ( 16,0) b) (6,0) c) (0,16) d) (16,1)
v) The co-ordinate of P, if D is taken as the origin, DA along negative direction of x-axis and DC along y-axis are
a) (12,2) b) (-12,6) c) (12,3) d) (6,10)
2) Four persons John, Saurabh, Salim and Ratan are sitting in a courtyard at points A, B, C and D respectively as shown in figure
The Courtyard has been divided into small squares by drawing equally spaced horizontal and vertical lines. Taking OX and OY as the coordinates axes answer the following questions.
i) The Co-ordinates of point A is
a) (4,3) b) (3, 4) c) (3,3) d) (4,4)
ii) The Co-ordinates of the point B are
a) (7,6) b) (7,7) c) ( 6,6) d) ( 6,7)
iii) the Co-ordinates of the point C are
a) (9,3) b) (9,4) c) (4,9) d) (10,4)
iv) The coordinates of point D are
a) (7,2) b) (8,2) c) ( 6,2) d) (2,7)
v) The distance between John and Salim is
a) 6 unit b) 4 units c) 5 units d) 7 units
vi) The distance between John and Sourav is
a) 6 units b) 3√2 unit c) 6√2 units d) 2√2 unit
vii) the distance between John and Ratan is
a) 2√5 units b) 2√10 units c) √5 units d) 20 units
3) For Maths integrated project, Sony created a symmetrical design on cartesian plain. She drew a fish in a rectangle ABCD in the second quadrant as shown in figure
Based on the above information p, answer the following questions:
i) Find the sum of abscissa of point A and B.
ii) find the area of the rectangle ABCD .
iii) what will be the new Co-ordinates of ABCD to draw the reflection of fish in the third quadrant across x-axis .
iv) What will be the new Co-ordinates of ABCD to draw the fish by shifting each vertex of the rectangle 5 units to the right?
4) Floor of Jenny's study room is paved with square tiles. She observed that 4 ants A, B, C and D are moving on the floor following a straight lines path.
Study the location of ants on the floor as shown in the figure considering two perpendicular edges of the floor as axes; their meeting point as origin and the floor surface as the first quadrant.Choose the correct option in the following questions:
i) Location of ants A, B, C and D in order are
a) (1,2),(2,3),(6,7),(8,9)
b) (2, 1),(3,2),(7, 6),(9,8)
c) (8,9),(6,7),(2,3),(1,2)
d) ( 9,8),(7,6),( 3,2),(2,1)
ii) Ants A, B, C and D are moving following the rule ?
a) x= y + 1 b) x + y = 1 c) y = x + 1 d) y= 2x
iii) Which of the following ordered pair does not lie on the line ?
a) (4,5) b) (7,8) c) ( 9,10) d) (8,7)
iv) Which of the following is true ?
a) the line passes through the origin,
b) The line meets x-axis at (0,1)
c) The line meets y-axis at (0,1). d) none
ASSERTION Reason
Each of the following examples contains STATEMENT-1 (Assertion) and STATEMENT-2 (Reason) has following four choice (a),( b),( c),( d), only of which is the correct answer. Mark the correct answer.
a) statement-1 is true, Statement -2 is true, statement-2 is a correct explanation for Statement-1 .
b) Statement -1 is true, statement-2 is true, statement-2 is not a correct explanation for statement-1.
c) statement-1 is true, statement-2 is false .
d) statement-1 the false , statement -2 is true.
1) Statement -1(A): The point P(0,-2) lies on y-axis
statement-2(R): Ordinates of every point on x-axis is zero. b
2) Statement -1(A): The point A (-4,0) lies on x-axis .
statement-2 (R): Ordinate of every point on x-axis is zero. a
3) Statement -1(A): The perpendicular distance of the point P(4,-7) from x-axis is 4.
Statement-2 (R): The perpendicular distance of a point from x-axis is the absolute value of its y-ordinate. d
4) Statement -1(A): point (-3,-3) lies on the angle bisectors of first and third quadrant angles .
Statement-2 (R): The numeric value of ordinates and abscissa of every point on the bisectors of first and third quadrant angles are equal. a
5) Statement -1(A): The point P(-7,0) lies on x-axis.
Statement-2 (R): the Ordinate of every point on y-axis is positive.
6) Statement -1(A): The point P(0,12) lies on y-axis 0.
Statement-2 (R): The abscissa of every point in y-axis is zero.
7) Statement -1(A): the perpendicular distance of the point (3,-7) from x-axis is 3.
Statement-2 (R): the perpendicular distance of the point (x,y) from x-axis |y|.
8) Statement -1(A): the co-ordinates of a point whose ordinate is -2 and abscissa is 5 are (-2,5).
Statement-2 (R): the Co-ordinates of a point lying on a positive x-axis at a distance of 9 units from the origin are (9,0) .
9) Statement -1(A): Points (3,-3) and (12,-4) lie on the same quadrant.
Statement-2 : (R): points (-1,-1) and (7,7) lie on the bisectors of 3rd and 1st quadrant angles .
Day - 10 (3/6/24)
A) Solve for x:
1) {√(x+2)+ √(x -3)}/{√(x+2)- √(x -3)} = 5.
2) {√(x+5)+ √(x -16)}/{√(x+5)- √(x -16)} = 7/3.
3) {√(7x)+ √(4x -3)}/{√(7x)- √(4x -3)} = 6.
4) 16{(a - x)/(a+ x)}³= (a+ x)/(a- x).
5) (x²+ 5x)/(3x²+1)= 14/13.
6) (3x²+ 5x +8)/(5x²+ 6x +12)= (3x +5)/(5x +6).
7) {√(x+a)+ √(x -b)}/{√(x+a)- √(x -b)} = (a + b)/(a- b).
8) {√(3x+7)+ √(3x)}/{√(3x+7)- √(3x)} = 7.
9) {√(5)+ √(5 - x)}/{√(5)- √(5 - x)} = 3.
10) (1- px)/(1+ px) . √{(1- qx)/(1+ qx)}= 1.
11) (a + √(a²- 2ax))/(a - √(a²- 2ax))= b.
12) If x= 2ab/(a+ b), a≠ b, find the value of (x+ a)/(x - a)+ (x +b)/(x - b).
13) If x= 4√6/(√2+ √3), find the value of (x+ 2√2)/(x - 2√2) + (x+ 2√3)/(x - 2√3).
14) If x= 6pq/p+ q), find the value of (x + 3p)/(x - 3p) + (x + 3q)/(x - 3q).
15) If p= 4xy/(x + y) find the value of (p+ 2x)/(p - 2x) = (p + 2y)/(p - 2y).
B) 1) a) Show that 3ax²- 2bx + 3a = 0 when x= {√(b +3a)+ √(b -3a)}/{√(b+3a)- √(b -3à)}.
b) Show that 3nx²- 2mx + 3n = 0 when x= {√(m +3n)+ √(m -3n)}/{√(m+3n)- √(m -3n)}.
2)a) If a+ c = 2b and 1/a + 1/d = 2/c, show that a: b:: c: d.
b) (4a + 7b)/(4a - 7b)= (4c + 7d)/(4c - 7d) then show that a/b = c/d.
3) If (a²+ b²)(m²+ n²)= (am + bn)², show a/m = b/n.
4) If x/b = y/b = z/c show that
a) x³/a³ - y³/b³ + z³/c³ = xyz/abc.
b) ³√{(lx⁻³ + my⁻³ + nz⁻³)/(la⁻³ + mb⁻³ + nc⁻³)}⁻¹
5) If y= {(p +1)¹⁾³ + (p -1)¹⁾³}/{(p +1)¹⁾³ - (p -1)¹⁾³} find the value of y³- 3py²+ 3y - p.
6) (ay - bx)/c = (CX - az)/b = (bz - cy)/a, show that x/a = y/b = z/c.
7) If ax = by = cz, show that x²/yz + y²/zx + z²/xy = bc/a² + ca/b² + ab/c²
8) x/{(b -c)(b + c - 2a)}= y/{(c - a)(c + a - 2b)}= z/{(a - b)(a+ b - 2c)} show that x + y + z= 0.
9) If (by + cz)/(b²+ c²)= (cz + ax)/(c²+ a²)= (ax + by)/(a²+ b²), then show that each ratio is equal to x/a = y/b = z/c.
10) Show: {(a- b)/c + (a- c)/b}² - {(d - b)/c + (d - c)/b}²= (a - d)²(1/c² - 1/b²).
11) If (b + c - a)/(y + z - x) = (c + a - b)/(z + x - y)= (a + b - c)/(x + y - z), then each of the ratio is equal to a/b = b/y = c/z.
12) If (a²+ c²)/(ab + CD) = (ab + cd)/(b²+ d²), then show that a/b = c/d.
C) If a/b = c/d = e/f, show that each of these is equal to:
1) (a + 3c- 5e)/(b + 3d - 5f)
2) {(a³- 2c³+ 3e³)/(b³- 2d³+ 3f³)}¹⁾³
3) {(a²+ c²+ e²)/(b²+ a²+ f²)}¹⁾²
4) (5a + 6b)/(5a - 6b)= (5c +6d)/(5c - 6d).
5) (a+ c +e)/(b + d+ f).
6) (a³+ c³+ e³)/(b³+ d³+ f³)= ace/bdf.
7) (a²b²+ c²d²+ e²f²)/(ab³+ cd³+ ef³)}³⁾²= √(ace/bdf).
8) Each ratio= √{(3a²+ 5c²- 7e²)/(3b²+ 5d²- 7f²)}.
9) (b²+ d²+ f²)(a²+ c²+ e²)= (ab + cd+ ef)².
10) (ab+cd + ef)²=(a²+ c²+ e²)(b²+ d²+ f²).
D) 1) If 8a + 9b : 8c + 9d :: 8a - 9b : 8c - 9d show that a, b, c, d are in proportion.
2) If a: b:: c: d show that (4a + 5b):(4a - 5b):: (4c + 5d): (4c - 5d).
3) If (2mc + 6mb + 3nc + 9nd)(2ma - 6mb - 3nc + 9nd)= (2ma - 6mb + 3nc - 9nd) (2ma + 6mb - 3nc - 9nd) then show that a, b, c,d are in proportional
4) If a, b, c are in continued proportion then prove
a) (a + b + c)(a - b - c)= a²+ b²+ c²
b) (a+ b + c)²/(a²+ b²+ c²)= (a+ b + c)/(a - b + c).
c) (a + b + c)(a - b+ c)= a²+ b²+ c²
d) (a+ b): (b + c):: a²(b - c): b²(a - b).
5) If a: b :: c: d, prove that
a) a+ b : c+ d :: √(a²+ b²): √(c²+ d²).
6) If a, b, c , d are in proportion, then prove that
a) a³+ c³+ e³: b³+ d³+ f³:: ace: bdf.
b) 4(a+ b)(c +d)= bd{(a+ b)/b + (c +d)/d}²
c) (ab + cd)²= (a²+ c²)(b²+ d²)
d) a: d :: (pa³+ qb³+ rc³): (pb³+ qc³+ rd³).
e) (a - b): (a + b):: (a - d): (a + 2b + 2c + d).
f) (b - c)²+ (c - a)²+ (d - b)²= (a - d)²
7) If a/b = b/c = c/d then show that
a) √{(a+ b+ c)(b+ c+ d)}/{√(ab)+ √(bc) + √(cd)}= 1
b) (a²+ b²+ c²)(b²+ c²+ d²)= (ab + bc + CD)²
c) a/d = (a - b)³/(b - c)³.
8) If a/b = c/d, show √{(a+ b + c)(b + c + d)}= √{(ab) + √(bc)+ √(cd)}.
9) If p/q = r/s , show that (2p + 3q)/(2p - 3q) = (2r + 3s)/(2r - 3s).
Day- 9 (2/6/24)
1) In what ratio is the line joining (2, -3) and (5,6) divided by x-axis. 1:2
2) In what ratio is the line joining (2, -4) and (-3, 6) divided by x-axis. 2:3
3) Calculate the Co-ordinates of the point P which divides the line joining A(-1,3) and B(5,9) in the ratio 1:2. (1,5)
4) The line joining the points A(-3, -10) and B(-2,6) is divided by the point P such that PB/AB = 1/5. Find the coordinate of P. (-11/5, 14/5)
5) P is a point on the line joining A(4,3) and B(-2,6) such that 5AP/2BP. Find the coordinates of P. (16/7,27/7)
6) In what ratio does the point P(3,3) divide the join of A (1,4) and B(7,1)? 1:2
7) In what ratio does the point (1,a) divide the join of (-1, 4) and (4,-1)? Also find the value of a. 2:3, 2
8) In what ratio does the point (a,6) divide the join of (-4,3) and (2,8)? Also find the value of a. 3:2, -2/5
9) In what ratio is the join of (4,3) and (2, -6) divided by x-axt. Also find the Co-ordinates of the point intersection. 1:2, (10/3,0)
10) Find the ratio in which the join of (-4,7) and (3,0) divided by y-axis. Also find the coordinates of the point of intersection. 4:3, (0,3)
11) Points A, B, C and D divide the line segment joining the point (5, -10) and origin in five equal parts. Find the coordinates of A, B , C and D. (4,-8), (3,-6),(2,-4),(1,-2)
12) Find the Co-ordinates of the points of trisection of the line joining the points (-3,0) and (6,6). (0,2),(3,4)
13) Show that the line segment joining the point (-5,8) and (10,-4) is trisected by coordinate axes.
14) Show that A(3,-2) is a point of trisection of the line segment joining the point (2,1) and (5,-8).
Also, find the coordinates of other point of trisection . (4,-5)
15) Given , two fixed points A(0,10) and B(-30 ,0). Calculate the coordinates of a point P which lies in the AB such that:
a) 2AP 3PB.
b) 3AP = AB
c) 7PB = AB
16) Given two fixed points P(-3,4) and Q(5,-2). Calculate the coordinates of points A and B in PQ such that:
5PA= 3PQ and 3PB = 2PQ.
17) The line segment joining A(2,3) and B(6,5) is intersected by x-axis at point K. Write down the ordinate of K. Hence, find the ratio in which K divides AB.
18) The line segment joining the points M(5,7) and N(-3,2) is interesting by y-axis at point L. Write down the absicca of L. Hence, find the ratio in which L divides MN.
Also the Co-ordinates of L.
19) Calculate the coordinates of points which devide the join of (8, 6) and (2,.3) into 4 equal parts. (13/2,21/4),(5,9/2) and (7/2,15/4)
20) A(2,5), B(-1,2) and C(5,8) are the coordinates of the vertices of the triangle ABC. Points P and Q lie on AB and AC respectively, such that :
AP: PB = AQ : QC= 1:2.
a) calculate the Co-ordinates of P and Q. (1,4)
b) Show that PQ= (1/3)BC
21) A(-3,4) B(3,-1) and C(-2,4) are the vertices of a triangle ABC. Find the length of line segment AP, where point P lies in side BC, such that BP: PC = 2:3.
Day- 8 (17/5/24)
Solve with the help of formula:
1) 2x²+ 3x-20= 0
2) 4x² - 12x + 9= 0.
3) 3x² -8x + 2= 0.
4) 2x + 2/x +5= 0
5) x + 96/x = 22.
6) x(2x +5) -3= 0
7) x(3x + 1/2) - 6 = 0
8) 3x(3x - 8)+ 16= 0
9) 4(x +2)(x +1)= 15.
10) One root of x² - 3x - c= 0 is -2, find the value of c and the other root.
11) One root of 2x²- 3(5x + c)= 0 is 3/2, find the value of c and other root.
Solve the following equations using formula
Give your answer correct to 2 decimal places.
1) x²+ 4x + 2 = 0.
2) 5x²- 3x- 7= 0.
3) x - 10/x = -7.
4) 2x + 5 = 9/x.
5) 3x(2x -7)= 4.
6) 2(x -1)(x -5)= 5.
7) 5(x +1)²+ 10(x +1)+ 3= 0.
8) (x -1)² -6(x -1)= 11.
9) Find the values of k for which the given equation has real and equal roots:
a) 12x²+ 4kx +3= 0.
b) kx² - 2 √5 x + 4= 0.
c) 4x²- 3kx + 1 = 0.
d) (k+1) x² - 2(k -1)x + 1 = 0.
10) Find the values of k for which the given equation has real roots.
a) 2x² - 5x- k = 0.
b) kx²+ 6x +1 = 0.
Day -7 (12/5/24)
Type -1
1) 2x²+ 2= 5x.
2) x²+ 9x - 52= 0
3) 6x²+ 5x - 4= 0.
4) 3x²+ 14x +8= 0
5) 7x²= 8 - 10x.
6) x(x +1)+ (x +2)(x +3)= 42.
7) 6x(3x -7)= 7(7- 3x).
8) 3(x²- 4)= 5x.
9) √3 x²+ 10x + 7 √3 = 0.
10) x²+ 2 √2 x - 6= 0
Type - 2
1) (x +3)/(x +2)= (3x -7)/(2x -3).
2) (x +2)/(x +3)= (2x -3)/(3x -7).
3) (5x +1)/(7x +5)= (3x +1)/(7x +1).
4) (3x -7)/(2x -5)= (x +1)/(x -1).
5) (x +1)/(x - 2)+ (x +11)/(x +3)= 4.
6) x/(x +1)+ (x +1)/x = 34/15, x≠ 0, x≠ -1
7) 6/(x +1 )+ 5/(2x +1)= 3
8) 4/(x -1)- 5/(x +2)= 3/x.
9) 5/(x -2)- 4/x = 3//(x +6).
10) (x +2)/6 - 1/(x +2)= 1/6.
11) x⁴- 10x² + 9= 0
12) x⁴- 25x² + 25= 0
13) 11/(5x -4) - 10/(4 - 5x)= 1
Type -3
1) Find the value of p in the following:
a) If (k+2)= 0 and 4k²+ kp²+ 82= 0.
b) If (2k -1)= 0 and k²+ 8kp²+ 2p= 0.
Type - 4
For each of the following solution set, find the quadric equation:
a) x= 2,3
b) x= 3, -4
c) x = 2, 2
d) x= 1/2, 1/3
Miscellaneous
1) Solve: x - 10/x = 9, if x= (a, b), then find
a) a+ b
b) ab
2) Find solution set of 2x² - 5 x - 3= 0, where x= (α, β). if the above quadratic equation is identical equal to ac²+ bx + c= 0, find a, b and c. Hence show that
a) α+ β = -b/a
b) α β = c/a
3) Find the solution set of 2x - 5/x = 3, x= (α, β). If the above quadratic equation is identical equal to ax² + bx + c= 0, find a, b and c. Hence show that
a) α + β = -b/a
b) α β = c/a
Day- 6 7/5/24
1) Factorize:
a) x³+ 6x²+ 11x +6
b) x³+ 2x² - x -2
c) x³ - 7x²+ 4x +12
d) 2x³+ 3x² - x - 4
2) Find the value of the constants a and b if x -2 and x +3 are factors of the expression x³+ ax²+ bx -12
3) Write the remainder when
a) 6x³ - 18x + 12 by x -1
b) x⁴+ x³ - 6 by x +2
c) 2b³ - b²+ 3b -4 by b+1
Day -5
1) Find the remainder when 2x³ - 3x² + 7x - 8 is divided by x - 2.
2) Find the value of x, which satisfies the inequation: - 2 ≤ 1/2 - 2x/3 ≤ 11/6, x ∈N. Graph the solution on the number line.
3) A function g is defined by g(x)=144 - 16x². Calculate g(2). Also find the value of x when g(x)= 0.
4) pretty deposited Rs 1500 per month in a bank for 8 months under the Recurring Deposit scheme. What will be the maturity value of her deposits , if the rate of interest is 12% per annum and interest is calculated the end of every month.
5) Solve: 3x²- 5x = 1.
6) The point A(4,7) was reflected in the origin to get the image A'
a) Write down the co-ordinate of A'.
b) if M is the foot of the perpendicular from A to the x-axis, find the coordinates of M.
c) If N is the foot of the perpendicular from A' to the axis, find the coordinates of N.
d) Name the figure AMA'N.
e) Find the area of the figure AMA'N.
7) Show: sinA(1+ tanA) + cosA(1+ cotA)= cosecA + secA.
8) Find x and y, if
A= 4 3 & B= x & C= 6
-5 0 -2 y with the relation AB = C.
9) Write down the equation of the line whose gradient is 4/3 and which passes through P, where P divides the line segment joining A(-2, -3) and B(5, 4), in the ratio 2 :5.
10) Factorize the expression with the help of Factor Theorem f(x)= 6x³- 7x²- 7x + 6. Hence, find the values of when f(x)= 0.
Day- 4
1) The point P(a, b) is reflected in the x-axis to obtain point Q(3, -4). Find a and b.
2) Solve using quadratic formula, x²- 5x -2= 0. Give your answer correct to three significant figures.
3) Find the value of k, if x - k is a zero polynomial of x³- kx²+ x + 4
4) Solve: 1< 3x - 3 ≤ 12, x ∈ R and mark it on a number line.
5) Prove: sinx/(1- cotx) + cosx/(1- tanx)= sinx + cosx.
6) A straight line passes to the points A(-2, 8) and B(10, -4). It interesects the coordinate axes at points E and the F. P is the midpoint of the segment EF. Find :
b) The co-ordinate of E and F.
c) The co-ordinates of the point P.
7) If A= a 3a B= 2 & C= 5
b 4b 1 12 with the relation AB = C, find a and b.
8) If A= 3 -2 B= 2a & C= -4 D= 2
-1 4 1 5 b with the relation AB+ 4C = 3D, then find a, b.
9) a)6x² - x = 35.
b) x²- 8x - 1280= 0
c) 1/(2y -9) = 1/(y - 3) + 4/5
d) 5ˣ⁺¹ + 5²⁻ˣ = 126
Day- 3
1) Calculate the amount receivable on maturity of a recurring deposit of Rs800 every month for 5 years 11% per annum.
2) A is the solution set of 8x - 11 > 4x - 3 and B is the solution set of 6x - 2≤ 4 x + 10 where x∈ N. Find the set A ∩ B. hence, graph the solution set on the number line.
3) List the elements of the solution set of the following inequation:
-3< x - 2 ≤ 9 - 3x; x∈R.
4) Solve the inequation |2x - 9|< 6, x∈ Z. State the solution set.
5) Solve: √(3x²+ x +5)= x -3.
6) Roots of the equation are (1/2) and -14. Find the equation.
7) 8(t² + 1/t²) - 42(t - 1/t) + 29= 0. Find the possible values of t.
8) Solve x²- 6x - 15= 0. Give your answer correct two decimal places.
9) A point P divides the join of A(6, -2) and B(-5, 8) in the ratio 2 : 3. Find the coordinates of P.
10) Find the ratio with x-axis divides the join of A(7, 2) and B(5, -4).
11) The coordinates of A and B are (3, -5) and (0, 4) respectively . Find (i) slope of AB. (ii) The equation of line passing through B and perpendicular to AB.
Day- 2
INEQUATION
1) State giving reasons whether the following statements are true or false:
i) if a > b, then a - c> b - c.
ii) if a < b, then AC < bc.
iii) if a >b, then a/c > b/c.
iv) if a - c< b - d, then a + d < b + c.
where a, b, c, d are real numbers & c≠ 0.
2) Solve each of the inquations given below and represent its solution set on a number line:
i) 2x - 1< 5, x ∈ R.
ii) 3x + 1 ≥ - 5, x ∈ R.
iii) 2(2x - 3) ≤ 6, x ∈ R.
iv) -4 < x< 4, x ∈ R.
v) -2 ≤ x < 5, x ∈ R.
3) Given x ∈ R {-3, -4, -5, -6} and 9≤ 1 -2x, find the possible values of x. Also represent its solution set on the number line.
4) Solve the inequation 3 - 2x ≥ x - 12, given that x ∈ N.
5) Find the smallest value of x, which satisfies the inequation 2x + 7/2 > 5x/3 + 3, x ∈ I.
6) if 10 - 5x <5(x + 6), find the smallest value of x, when
i) x ∈ R. ii) x ∈ W c) x ∈ N
7) List the elements of the solution set of the inequation -3 < x -2≤ 9 - 2x, x ∈ N.
8) P is the solution set of 8x - 1 > 5x + 2 and Q is the solution set of 7x - 2 ≥ 3(x + 6), where x ∈ N. Find the set P ∩ Q.
9) Solve each of the inequation given below and represent the solution set on the number line:
a) 2x + 3 ≤ 3x + 1, x ∈ R.
b) (5 x - 8)/3 ≥ (4x -7)/2, x ∈ R.
c) 5x/4 - (4x - 1)/3 > 1, x ∈ R.
d) 2 ≤ 2x-3 ≤ 5, x ∈ R.
e) 2x -5 ≤ 5x+4< 11, x ∈ R.
f) -2/3 < 1 + x/3 ≤ 2/3, x ∈ R.
10) Solve each of the following inequation and represent the solution set on the number line:
a) 5x -11 ≤ 7x - 5< 9
b) 2x -1 ≥ x + (7 - x)/3 > 2.
11) What do the following graphs represent ? Write the relevant inquality.
Represent A and B on the number line. Find
a) A ∩B
b) A' ∩ B.
13) If P is the solution set of -3x + 4< 2x - 3, x ∈ N, and Q is the solution set of 4x -5 < 12, x ∈ W, find
a) P ∩Q
b) Q - P
14) Solve the inequation 3 - 2x ≥ x - 12, given that x ∈ N.
15) Find the range of the values of x, which satisfy the inequality -1/5 ≤ 3x/10 + 1 < 2/5, x ∈ R.
Graph the solution set on the number line.
16) Solve the following inequation, and graph the solution set on the number line:
2y - 3 < y +2 ≤ 3y +5, y(-R).
17) Given that x ∈ I, solve the inequation and graph the solution on the number line:
3 ≥ (x - 4)/2 + x/3 ≥ 2.
18) If x ∈ Z, find the solution set for the inquation 5 < 2x - 3≤ 14 and graph it on a number line.
19) Solve 2< 2x - 3 ≤ 5, x ∈ R and mark it on a number line.
20) Solve the following inequation, and graph the solution on the number line:
2x - 5 ≤ 5x + 4 < 11, x ∈ R.
21) Find the values of x, which satisfy the inequation: - 2 ≤ 1/2 - 2x/3 ≤ 11/6, x ∈ N. Graph the solution set on the number line.
22) Solve the inequation: - 3 ≤ 3 - 2x < 9, x ∈ R. Represent your solution on a number line.
23) Solve the inequation 12 + 11x/6 ≤ 5+ 3x, x ∈ R. Represent the solution on a number line.
24) Given P= {x: 5< 2x -1 ≤ 11, x ∈ R}, Q= {x : -1≤ 3+ 4x < 23, x ∈ I}
Where R= {real number}, I={integer}.
Represent P and Q on number lines . Write down the elements of P ∩Q.
25) The diagrams represent two inequation A and B on real number lines .
a) Write down A and B in the set builder notation.
b) Represent A ∩ B and A ∩ B' on two different number lines.
Day- 1
1) Amit deposited Rs150 per month in a bank for 8 months under the Recurring Deposit Scheme. What will be the maturity value of his deposits, if the rate of interest is 8% p.a and interest is calculated at the end of every month ? Rs1236
2) Lakshmi took a Cumulative Time Deposit Account of Rs240 per month at 10% p.a. She received Rs3840 on maturity. Find the period for this account. 15 months
3) Manoj opened a Recurring Deposit Account in a bank and deposited Rs500 per month for 3 years . The bank paid him Rs20220 on maturity. Find the rate of interest paid by the bank. 8%
4) Rajeev opens a Recurring Deposit Account with the bank of Rajasthan and deposits Rs600 per month for 20 nonths. Calculate the maturity value of this account, if the bank pays interest at the rate of 10% per annum. Rs13050
5) Miss Anshu Pandey deposited Rs350 per months for 20 months Recurring Deposit Scheme. Find the total amount payable by the bank on maturity of the account if the rate of interest is 11% per annum. Rs7673.75
6) Mr Mathew opened a Recurring Deposit Account in a bank with Rs500 per month 5/2 years. Find the amount she will get on maturity if the interest is paid on monthly balance at 12.5% per annum . Rs17421.87
7) Calculate the amount received on maturity of a recurring deposit of Rs150 per month for 1 year 6 months. If the rate of interest is 11% per annum. Rs2935.13
8) Amar deposits Rs 1600 per month in Recurring Deposit for 3 years at the rate of 9% p.a simple interest. Find the amount will get at the time of maturity. Rs65592
9) A Recurring Deposit Account of Rs1200 per month has a maturity value of Rs12440. If the rate of interest is 8% and the interest is calculated at the end of the every month. Find the time (in months) of this Recurring Deposit Account . 10
10) Sujata deposited a certain sum of money, every month, for 5/2 years in a Cumulative Time Deposit Account. At the time of maturity she collected Rs4965. If the rate of interest was 8% p.a. Find the monthly deposit. Rs150
11) Sumit paid Rs 300 per month in Recurring Deposit Account for 2 years . He received Rs7875 as the maturity amount. Find the rate of interest. 9%
12) Meena has a Recurring Deposit Account of Rs340 per months at 6% per annum. If she gets Rs 7157 at the time maturity. Find the total time for which account was held. 20months
13) On depositing Rs200, every month in a Recurring Deposit Account, paying 9% per annum, a person collected Rs2517 at maturity . Find the period. 12 months


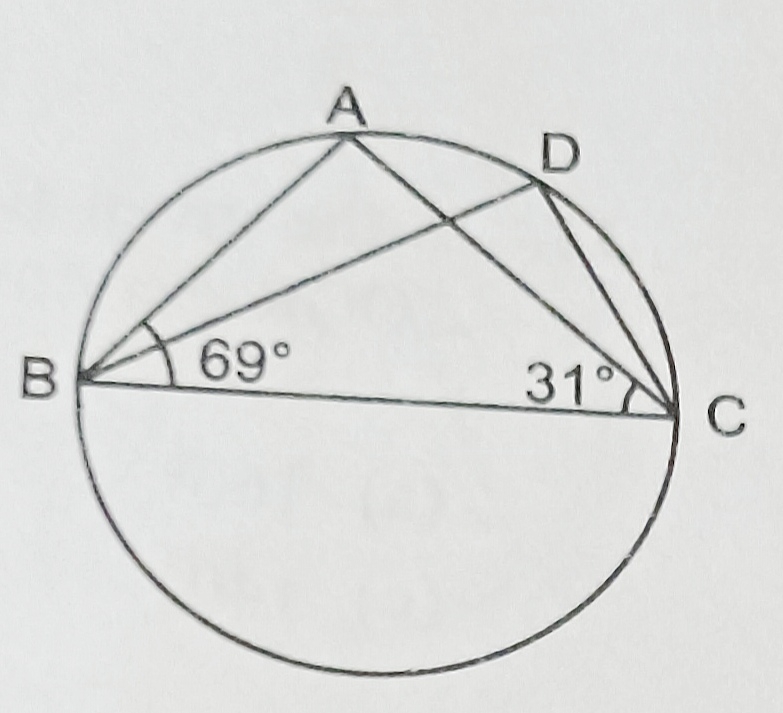



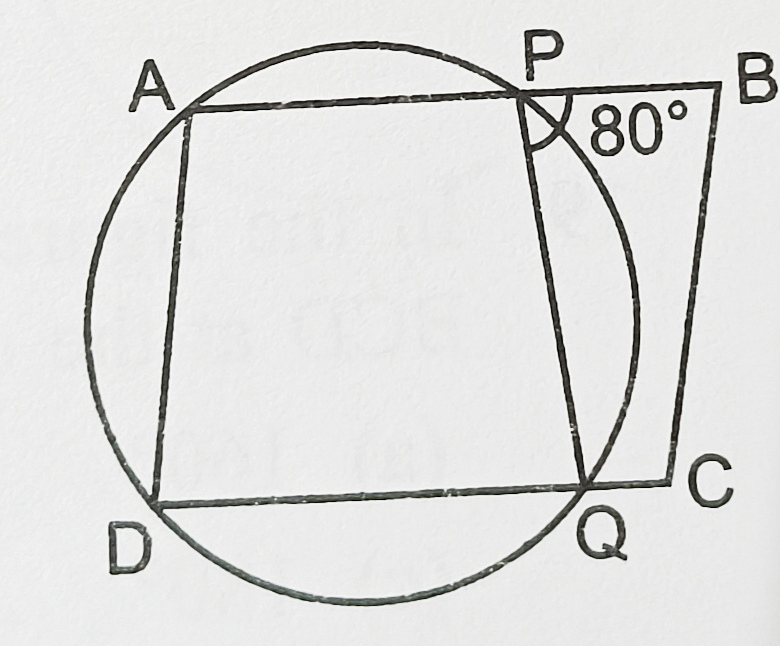
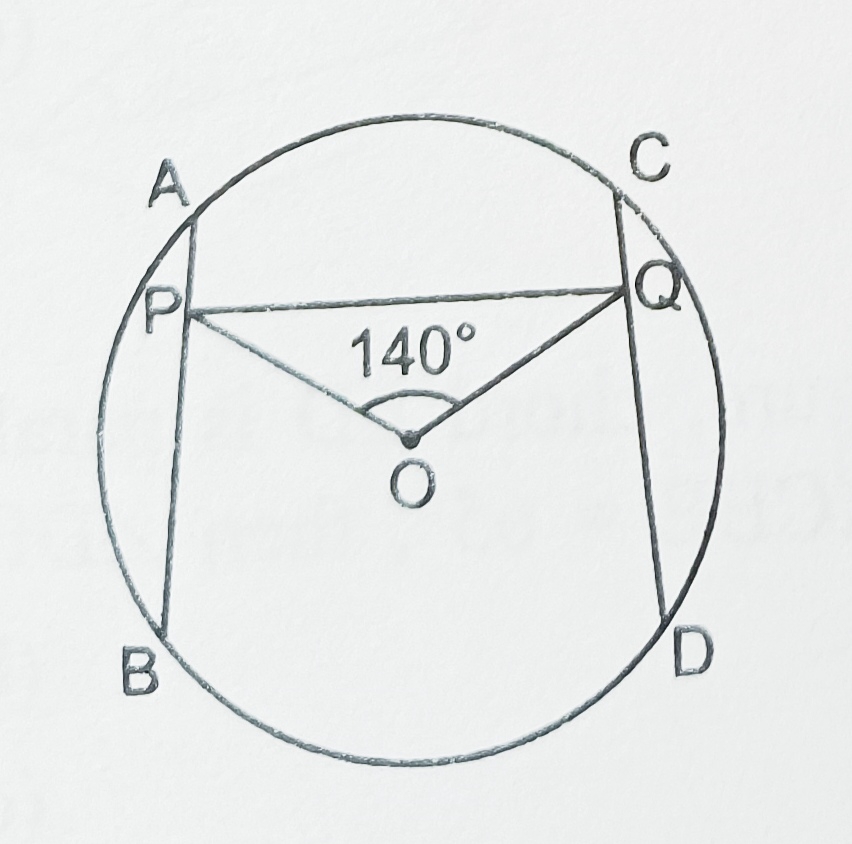














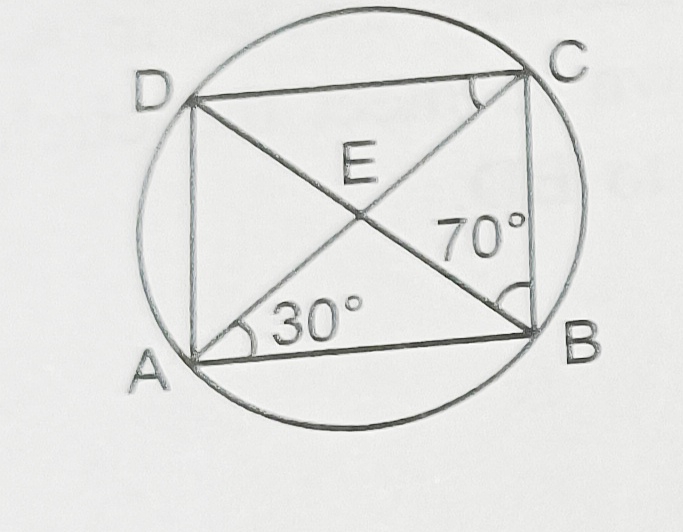
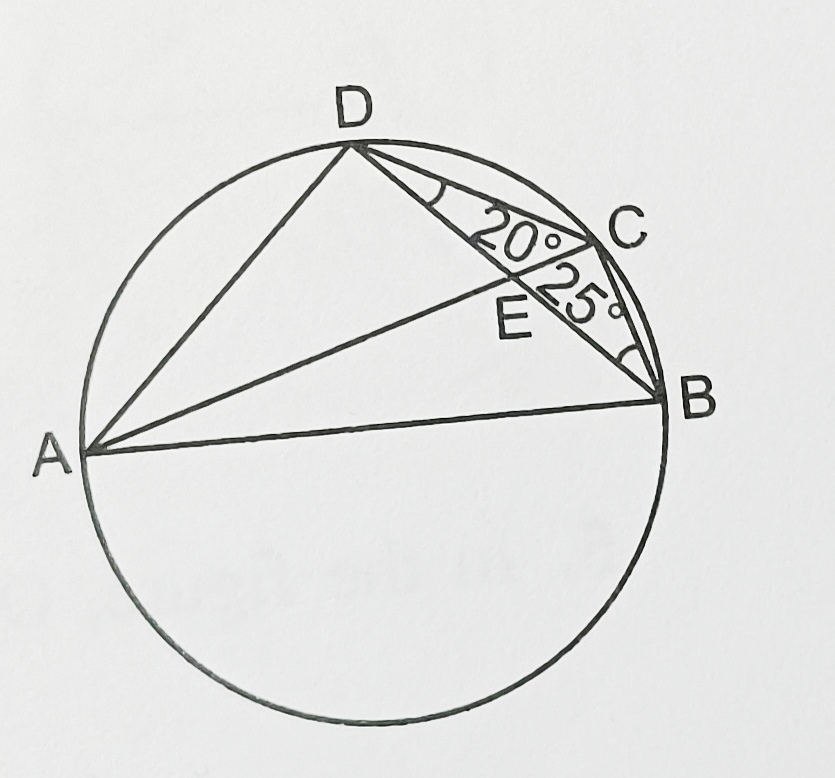


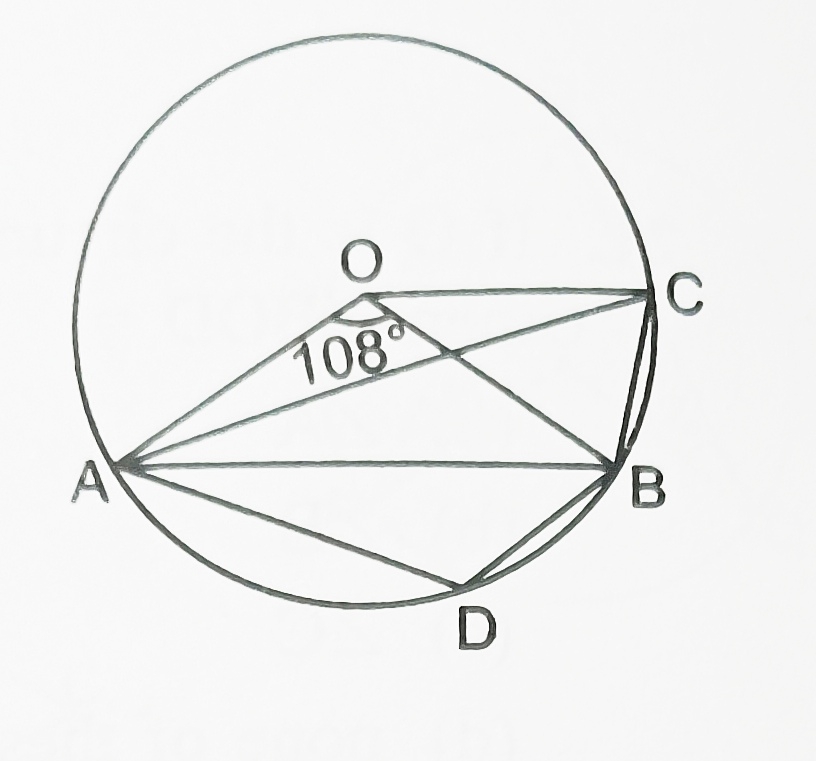


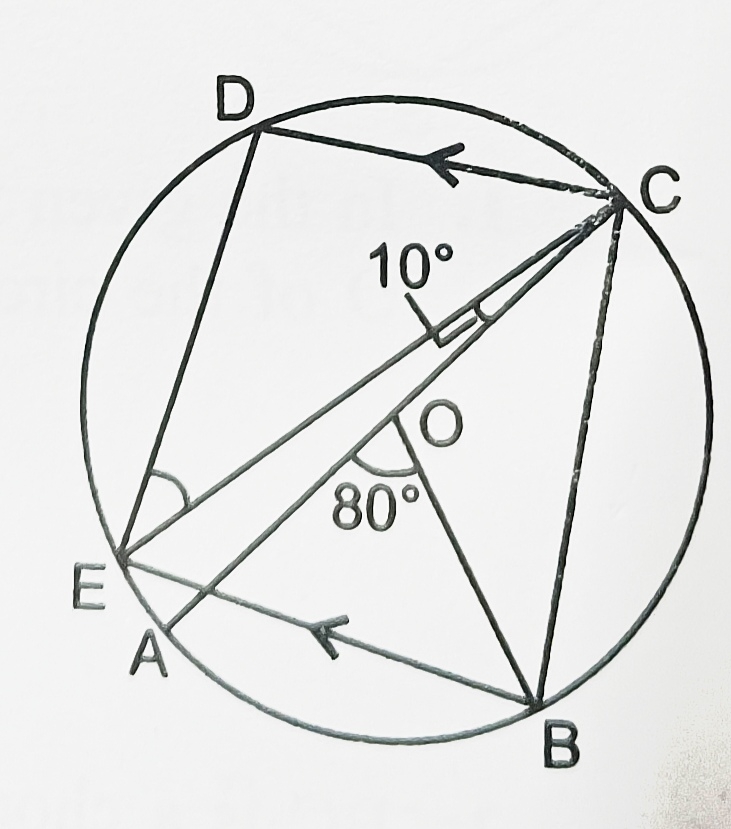







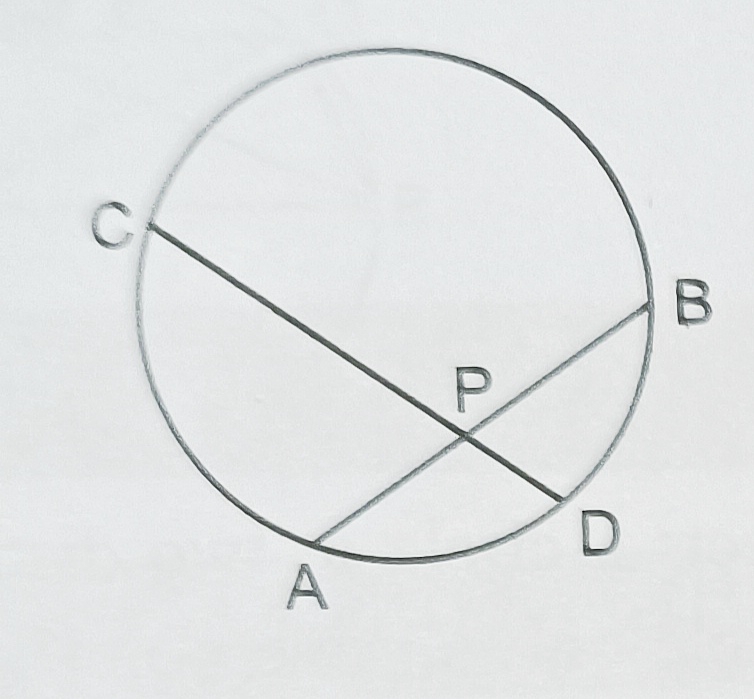





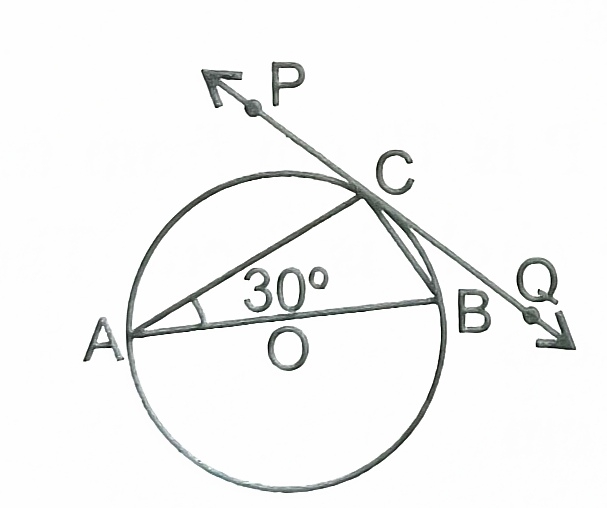





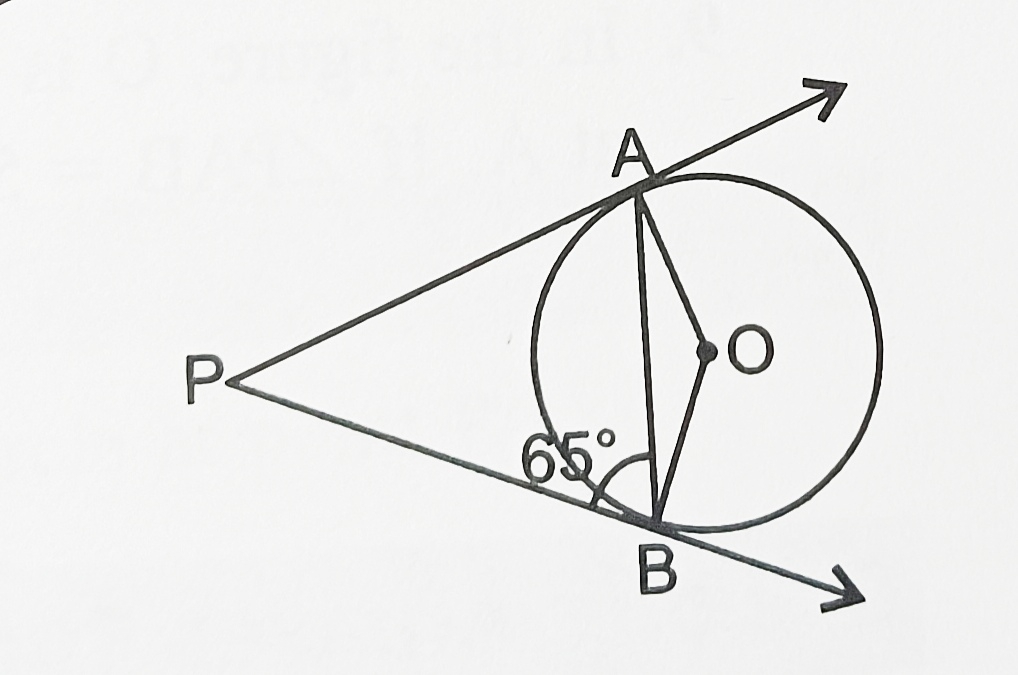

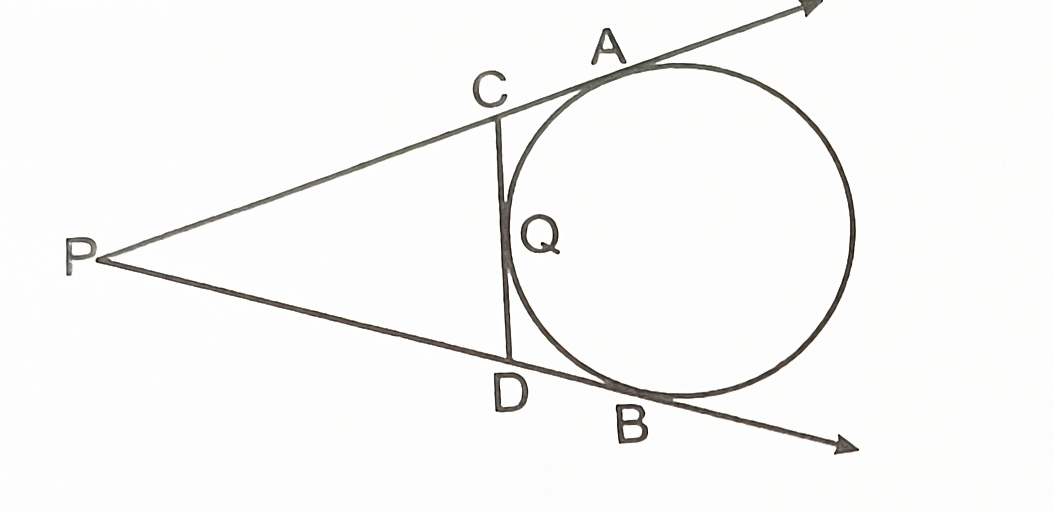







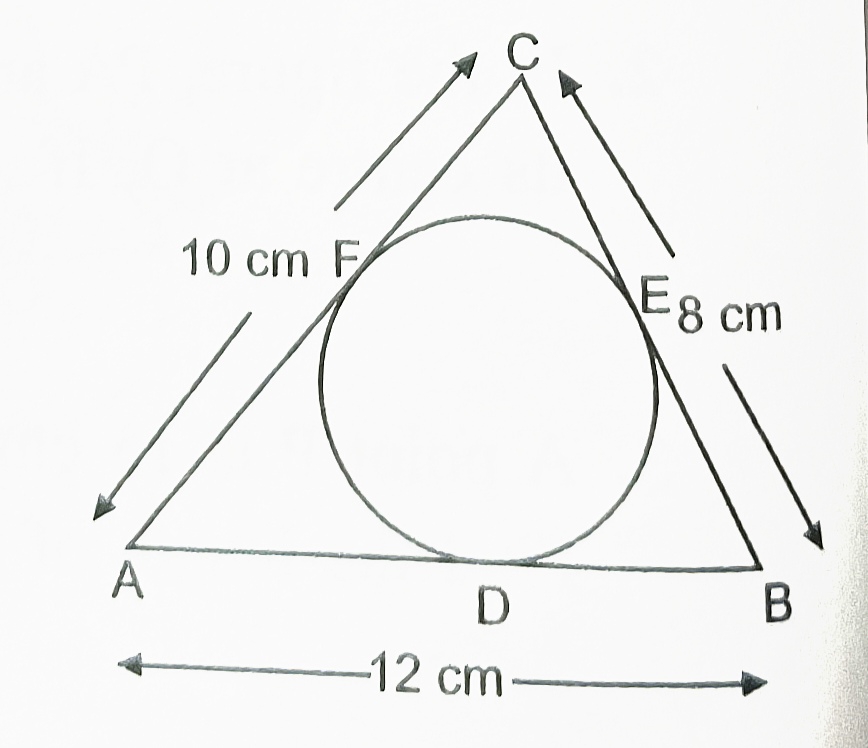








































































No comments:
Post a Comment